Уравнение состояния идеального газа
Д.И.Менделеев придал этой формуле общую форму, воспользовавшись законом Авогадро. Пусть масса газа равна 1 кмоль, тогда:
Поведение реальных газов можно описать уравнением Ван-дер-Ваальса:
,
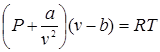Майер на основе опытных данных установил эквивалентность между теплотой и работой:
, (2.1)
где А – коэффициент пропорциональности.
математическим выражением первого закона термодинамики:
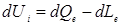, (2.2)
где U – внутренняя энергия системы.
Работу расширения и сжатия, где
.
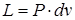Следовательно, выражение (2.3) для одного килограмма газа примет вид:
.
В изохорном процессе все подводимое тепло идет на увеличение внутренней энергии газа
; 
.
; 
первое математическое выражение первого закона термодинамики примет вид:
.
Первый закон термодинамики через энтальпию
второе математическое выражение первого закона термодинамики:
.
уравнение Майера:
.
На практике важное значение имеет величина показателя адиабаты К, который равен:
. (2.16)
Из молекулярно – кинетической теории газов вытекает:
- для одноатомных газов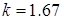 
;
- для двухатомных газов 
;
- для трех- и многоатомных газов 
.
Для процессов протекающих при постоянном давлении установили, что 
, отсюда
.
Зная величину показателя адиабаты можно определить теплоемкости различных веществ:
; 
.
Изменение внутренней энергии определяется по общей формуле:
.
Изохорный процесс. Доля теплоты, идущей на изменение внутренней энергии:
.
Изобарный процесс.Доля теплоты, идущая на изменение внутренней энергии:
,
где k – показатель адиабаты.
уравнение изотермы:
; α=0
уравнение адиабаты:
.
уравнение политропы:
.
Теплоемкость газов в политропном процессе
1) в изохорном процессе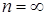 
получаем, что
.
Вычтем из обеих частей уравнения по единице, получим:
;
.
2) в изобарном процессе n= 0 получаем, что
;
.
3) в изотермическом процессе n= 1 получаем, что
;
.
4) в адиабатном процессе n=k получаем, что
;
.
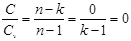уравнение политропы
термического КПД:
термического КПД цикла Карно:
Степень расширения (сжатия) - это отношения большего объема к меньшему объему в процессе:
.
Для оценки эффективности работы холодильных машин служит холодильный коэффициент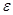 
:
.
термического КПД обратимого и необратимого циклов имеет вид:
.
Термический КПД обратимый цикл
. Термический КПД обратимого цикла
Интегральная сумма приведенных теплот
=> Клаузиус назвал энтропией S 
для обратимых и необратимых циклов общее выражение для приведенной теплоты примет вид:
;
.
Для обратимого адиабатного процесса:
, то есть 
изменение энтропии для изотермических, изохорных процессов;
изменение энтропии для изобарных процессов
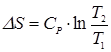
угловые коэффициенты изохоры и изобары
; 
.
Изменение энтропии в политропном процессе можно определить по формуле:
;
значение углового коэффициента для политропных процессов:
.
..
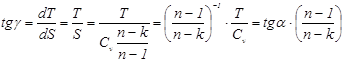