Измерение информации. Классификация мер.
Синтаксические меры информации.
Основой представления информации в той или иной знаковой системе (языке) является ее алфавит
Алфавит – фиксированный конечный набор символов любой природы
Чем из большего количества символов состоит алфавит, тем большее количество информации несет один знак.
Полное число символов алфавита принято называть мощностью алфавита.
Мощность алфавита - полное число символов алфавита
Например, алфавит русского языка содержит 33 символа-буквы, алфавит десятичной системы счисления основан на 10 арабских цифрах, алфавит двоичной системы счисления состоит из 0 и 1.
Автор статистической теории информации американский инженер и математик Клод Шеннон предложил формулу для вычисления количества информации для событий с различными вероятностями.
Чем меньше вероятность появления события (сигнала), тем больше информации оно несет для потребителя. Этот факт можно выразить следующей формулой (формула Шеннона):
 |
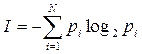где I – количество полученной информации при передаче сообщения;
pi – вероятность появления события (сигнала) с номером i;
N – количество возможных сигналов.
 |
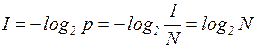В частном случае равновероятных событий, когда вероятность появления сигнала
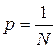, получается формула Ральфа Хартли
При равновероятных событиях получаемое количество информации максимально. А соответствующее число событий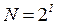 
Рассмотрим несколько случаев.
Пусть в системе возможно только одно событие. Свяжем с реализацией события сигнал. Тогда N = 1, и количество полученной информации I = 0. Тот факт, что событие наступит, безусловно, обязательно, не несет никакой информации.
 |
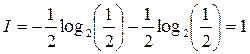Если для кодирования события используется двоичная система счисления с алфавитом мощности N =2, содержащим 0 и 1, а вероятности появления 0 или 1 равны
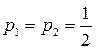, то
Количество информации I = 1, связанное с появлением 0 или 1 и принято в качестве единицы измерения информации «бит» (от англ. BInary digiT – двоичная единица).
При обработке информации часто возникает необходимость представлять средствами одного алфавита символы других алфавитов. Такое представление носит название «кодирование». Простейшим абстрактным алфавитом, достаточным для кодирования любого другого алфавита, является двоичный алфавит, образованный двумя символами-цифрами 0 и 1.
Если каждый символ некоторого алфавита кодируется комбинацией n двоичных цифр, то с его помощью можно закодировать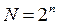 
различных символов (N – мощность производного алфавита)
Например, в системе кодирования ASCII для представления символов других алфавитов используется n =8 бит. Это значит, с помощью таких двоичных комбинаций можно закодировать 256 символов, чего оказывается вполне достаточно для кодирования большинства реальных алфавитов. Последовательность из 8 бит получила специальное название – байт.
В другой распространенной системе кодирования Unicod для кодирования символов используется комбинация из двух байтов, что еще больше расширяет возможности кодирования символов в двоичной системе счисления.
ASCII 8 бит
Unicod 16 бит
Последовательность из 8 бит получила специальное название – байт.
Обычно приставка “кило” означает тысячу, а приставка “мега” - миллион, но в вычислительной технике все «привязывается» к принятой двоичной системе кодирования.
В силу этого один килобайт равен не тысяче байтов, а 210 = 1024 байтов.
1 Мб = 210 Кб = 1024 Кб = 220 байт = 1 048 576 байт.
1 Гб = 210 Мб = 220 Кб = 230 байт = 1 073 741 824 байт.
Допустим, что в некоторой системе кодирования используется алфавит, состоящий из 16 символов (для кодирования одного символа отводится 4 бита). Какой объем данных займет информационное сообщение, состоящее из 4096 символов?
Мощность алфавита, используемого для записи этого сообщения составит 16 (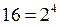
). Количество информации, приходящейся на один символ по формуле Хартли-Шеннона:
 |
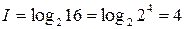Объем данных VД составит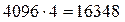 
бит или 
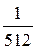Мб.
Объектами двоичного кодирования могут служить не только символы текстового сообщения, но и элементы графического изображения – пиксели. Цветные изображения могут иметь различные режимы: 16 цветов (2 4), 256 цветов (2 4), 1024 цвета (2 10), 65536 цветов (high color) (2 16), 16777216 цветов (true color) (2 24). Количество бит на точку (пиксель), например, режима «high color», равно 16, что обеспечивает весьма широкую палитру графического изображения.
Пусть количество цветов, воспроизводимых на экране сотового телефона, равно 1024, а разрешение экрана 128×64.
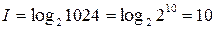Рассчитаем количество информации, приходящейся на одну точку (пиксель) экрана сотового телефона по формуле Хартли-Шеннона:
бит
 |
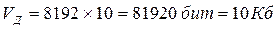По условию задачи экран имеет размер 128×64, т.е. всего на экране 8192 (точек). Рассчитаем необходимый объем видеопамяти (объем данных):
В работах Р.Хартли и К.Шеннона информация возникает перед нами лишь в своей внешней оболочке, которая представлена отношениями сигналов, знаков, сообщений друг к другу - синтаксическими отношениями. Количественная мера Хартли-Шеннона не претендует на оценку содержательной (семантической) или ценностной, полезной (прагматической) сторон передаваемого сообщения
Эта мера количества информации оперирует с обезличенной информацией, не выражающей смыслового отношения к объекту.
