Случайная величина 
распределена по нормальному закону, если ее плотность распределения вероятностей
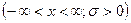(1), где 
- математическое ожидание, 
- среднее квадратическое отклонение .
Вероятность того, что примет значение, принадлежащее интервалу 
, равна
(2), где
-функция Лапласа.
Вероятность того, что абсолютная величина отклонения нормально распределенной случайной величины от ее математического ожидания не превысит положительного числа 
, равна
(3).
Задача 1.
На станке изготавливаются шарики для подшипников. Номинальный диаметр шарика 
. Фактический размер диаметра шарика вследствие неточности изготовления представляет собой случайную величину , распределенную по нормальному закону с математическим ожиданием 
и средним квадратическим отклонением 
. Найти:
а) процент шариков для подшипников, которые будут иметь диаметр от 4,8 до 5 мм;
б) процент брака, если известно, что при контроле бракуются все шарики, диаметр которых отклоняется от номинального больше, чем 0,1 миллиметра.
Указание: для пункта а использовать формулу (2), для пункта б использовать формулу (3) и рассматривать противоположное событие – шарик не будет забракован.
Ответ: а) 
; б) 
Задача 2.
Длина початка – один из главных показателей продуктивности кукурузы. Выявлено, что у растений кукурузы сорта Чиквантино длина початка представляет собой случайную величину , распределенную по нормальному закону с математическим ожиданием 
. У 68,26 % растений кукурузы этого сорта длина початка принимает значение, принадлежащее интервалу 
см. Какой процент растений кукурузы этого сорта имеет длину початка более 14,1 см?
Указание: подставив исходные данные в формулу (2) получим уравнение
.
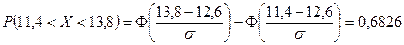Выполнив преобразования находим 
.
Далее необходимо решить это уравнение в mathcad
|
После 0,3413 нажать одновременно ctrl и = и затем 
. Затем поставить курсор около x и выполнить команду: symbolic 
variable solve.
Получим, что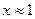 
, значит 
и 
.
Далее необходимо определить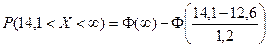 
. Это можно определить в mathcad.
Ответ: 10,56 %.
Задача 3.
Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону распределения со средним квадратическим отклонением 
найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине 10 г.
Указание: использовать формулу (3).
Ответ: 0,383.
Задача 4.
Настриг шерсти у овец асканийской породы представляет собой случайную величину ,распределенную по нормальному закону. Практически все возможные значения этой величины принадлежат интервалу 
кг. Найти интервал, симметричный относительно математического ожидания, в котором с вероятностью 0,95 заключены возможные значения шерсти у овец этой породы.
Указание: надо использовать закон трех сигм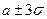 
и потом можно перейти к системе уравнений
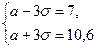Решив эту систему найдем и и далее можно использовать формулу (3).
|
|
|
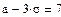
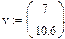
| решение системы линейных уравнений |
|
|
|
|
|
| далее аналогично задаче 3 |
|
|
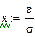
