К кулоновским силам применим рассмотренный в механике принцип независимости действия сил – (1). F = Q 0 E и F i = Q 0 Е i. Подставляя выражения в (1), получаем (2). Формула (2) выражает принцип суперпозиции электростатических полей, согласно которому напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.
 (1)
(1)  (2)
(2)  (3)
(3)  (4)
(4)
Принцип суперпозиции применим для расчета электростатического поля электрического диполя. Электрический диполь – система двух равных по модулю разноименных точечных зарядов, расстояние между которыми значительно меньше расстояния до рассматриваемых точек поля. Вектор (3) называется электрическим моментом диполя. Согласно принципу суперпозиции, напряженность Е поля диполя в произвольной точке – (4).
Теорема Гаусса для электростатического поля в вакууме
Поток вектора напряженности сквозь сферическую поверхность радиуса r, охватывающую точечный заряд Q, находящийся в ее центре, равен (1). Для поверхности любой формы, если она замкнута и заключает в себя точечный заряд Q, поток вектора Е будет равен Q/ e0. Рассмотрим общий случай. В соответствии с принципом суперпозиции – (3). Каждый из интегралов, стоящий под знаком суммы, равен Qi / e0, следовательно, (4).
 (1)
(1)  (3)
(3) 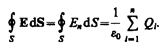 (4)
(4)
Формула (4) выражает теорему Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на e0.
Применение теоремы Гаусса для расчета электростатического поля заряженной сферы
Сферическая поверхность заряжена равномерно с поверхностной плотностью +s. Благодаря равномерному распределению заряда поле, создаваемое им, обладает сферической симметрией. Поэтому линии напряженности направлены радиально. Построим мысленно сферу радиуса r, имеющую общий центр с заряженной сферой. Если r>R, то внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле, и, по теореме Гаусса,  , откуда (1).
, откуда (1).
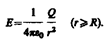 (1)
(1)
Применение теоремы Гаусса для расчета электростатического поля заряженного шара
Шар радиуса R с общим зарядом Q заряжен равномерно собъемной плотностью r. Учитывая соображения симметрии, можно показать, что для напряженности поля вне шара получится тот же результат, что и в предыдущем случае с заряженной сферой. Внутри же шара напряженность поля будет другая. Поэтому, согласно теореме Гаусса, получаем (1).
 (1)
(1)






