Матрицы
Основные сведения
Матрицей размера (порядка)  или
или  -матрицей называется прямоугольная таблица чисел, содержащая
-матрицей называется прямоугольная таблица чисел, содержащая  строк и
строк и  столбцов. Числа, составляющие матрицу, называются элементами матрицы.
столбцов. Числа, составляющие матрицу, называются элементами матрицы.
Матрицы обозначаются прописными буквами латинского алфавита, например,  , а для обозначения элементов матрицы используются соответственно строчные буквы с двойной индексацией:
, а для обозначения элементов матрицы используются соответственно строчные буквы с двойной индексацией:  ,
,  ,
, 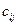 ,…, где
,…, где  - номер строки,
- номер строки,  - номер столбца.
- номер столбца.
 (1.1)
(1.1)
или в сокращенной записи  ,
,  .
.
Наряду с круглыми скобками используются и другие обозначения:  .
.
Элементы  образуют главную диагональ матрицы.
образуют главную диагональ матрицы.
Виды матриц
Если 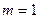 , то
, то  - матрица (вектор)-строкa, или просто строка размера
- матрица (вектор)-строкa, или просто строка размера  .
.
Если  , то
, то  – матрица (вектор)-столбец, или просто столбец размера
– матрица (вектор)-столбец, или просто столбец размера  .
.
Если  , то
, то 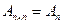 - квадратная матрица
- квадратная матрица  -го порядка.
-го порядка.
Если  при
при  , то
, то  - диагональная матрица:
- диагональная матрица:
 .
.
В частности, при  матрица
матрица  называется скалярной.
называется скалярной.
Если  , то
, то  (или
(или  ) – единичная матрица
) – единичная матрица  - го порядка:
- го порядка:

Если  , то
, то  (или
(или  ) – нулевая матрица, или нуль-матрица:
) – нулевая матрица, или нуль-матрица:  .
.
Если все элементы квадратной матрицы под (над) главной диагональю равны нулю, то матрица  называется верхней (нижней) треугольной матрицей:
называется верхней (нижней) треугольной матрицей:
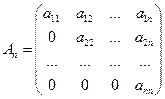 ,
, 
 - верхняя треугольная,
- верхняя треугольная,  - нижняя треугольная матрица.
- нижняя треугольная матрица.
Равенство матриц. Матрицы 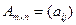 и
и  равны, если
равны, если  ,
,  .
.
Операции над матрицами
1. Умножение матрицы на число. Произведением матрицы 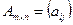 на число
на число  называется матрица
называется матрица  такая, что
такая, что 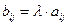 ,
,  .
.
Например,  .
.
В частности,  .
.
Следствие. За знак матрицы можно выносить общий множитель всех ее элементов.
2.Сложение матриц. Суммой двух матриц 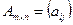 и
и  называется матрица
называется матрица  такая, что
такая, что  ,
,  , т.е. матрицы складываются поэлементно.
, т.е. матрицы складываются поэлементно.
В частности,  .
.
3. Умножение матриц. Произведением матрицы  на матрицу
на матрицу  называется матрица
называется матрица  такая, что
такая, что  ,
,  , т.е. каждый элемент
, т.е. каждый элемент 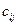 матрицы
матрицы 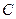 равен сумме произведений элементов
равен сумме произведений элементов  -ой строки матрицы
-ой строки матрицы  на соответствующие элементы
на соответствующие элементы  - го столбца матрицы
- го столбца матрицы  .
.
Из определения следует, что для умножения матрицы  и
и  должны быть согласованными, т.е. число
должны быть согласованными, т.е. число 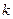 столбцов матрицы
столбцов матрицы  должно быть равно числу
должно быть равно числу 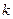 строк матрицы
строк матрицы  .
.
Пример 1. Даны матрицы  и
и  . Найти
. Найти  и
и  .
.
Решение: Размер матрицы произведения  .
.
Вычислим элементы матрицы  , умножая элементы каждой строки матрицы
, умножая элементы каждой строки матрицы  на соответствующие элементы столбцов матрицы
на соответствующие элементы столбцов матрицы  :
:
 .
.
Аналогично  .
.
Получили, что произведения матриц  и
и  существуют, но являются матрицами разных порядков.
существуют, но являются матрицами разных порядков.
Свойства операций над матрицами.
10.  20.
20. 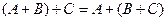 30.
30. 
40.  50.
50.  60.
60. 
70.  80.
80. 
Целая положительная степень  (
( ) квадратной матрицы есть
) квадратной матрицы есть  .
.
По определению  .
.
Особенности операций над матрицами.
1. Коммутативный (переместительный) закон умножения в общем случае не выполняется, т.е.  .
.
Если 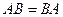 , то матрицы
, то матрицы  и
и  называются перестановочными.
называются перестановочными.
В частном случае коммутативным законом обладает произведение любой квадратной матрицы  на единичную матрицу
на единичную матрицу  того же порядка, причем
того же порядка, причем  .
.
2. Произведение двух ненулевых матриц либо  -я степень ненулевой матрицы может быть нулевой матрицей.
-я степень ненулевой матрицы может быть нулевой матрицей.
3. Равенство произведений матрицы  на матрицы
на матрицы  и
и 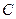 не обязательно означает, что
не обязательно означает, что  , т.е. если
, т.е. если  и
и  , то не обязательно
, то не обязательно  .
.
4. Если матрицы  и
и  - перестановочные, то
- перестановочные, то 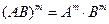 .
.
Выражение вида  , где
, где  и
и  - соответственно квадратная и единичная матрица одинакового размера;
- соответственно квадратная и единичная матрица одинакового размера;  - числа, называется полиномом (многочленом) от матрицы
- числа, называется полиномом (многочленом) от матрицы  . Он представляет собой матрицу, которую можно рассматривать как результат подстановки матрицы вместо переменной
. Он представляет собой матрицу, которую можно рассматривать как результат подстановки матрицы вместо переменной  в обычный многочлен степени
в обычный многочлен степени  :
:  .
.
Если при подстановке матрицы  вместо
вместо  в многочлен
в многочлен  получается нулевая матрица, то матрица
получается нулевая матрица, то матрица  называется корнем многочлена
называется корнем многочлена  , а сам многочлен - аннулирующим многочленом для матрицы
, а сам многочлен - аннулирующим многочленом для матрицы  .
.
Транспонирование матрицы – переход от матрицы  к матрице
к матрице  (или
(или  ), в которой строки и столбцы поменялись местами с сохранением их порядка. Матрица
), в которой строки и столбцы поменялись местами с сохранением их порядка. Матрица  ( или
( или  ) называется транспонированной.
) называется транспонированной.
Например, если  , то
, то  .
.






