Класична математика є дуже потужним апаратом для розв’язання науково-технічних задач. Але не всі сфери людської діяльності допускають достатню ступінь формалізації для використання цього апарату. Людина постійно приймає рішення в соціальних процесах, опис яких характеризується неповнотою, нечіткістю та невизначеністю. Зокрема це стосується процесів соціально-економічної сфери. Основною діючою фігурою в цій сфері є людина-фахівець, яка мислить і оперує частіше за все нечіткими, нематематичними категоріями, наприклад, “у світі ще з кінця XIX сторіччя потреби практики різко посилювали увагу до інструментальних, практичних аспектів аналітичної економії, до питань функціонування ринкової економіки”.
Теорія нечітких множин дає змогу до певної міри формалізувати процеси і явища соціальної, економічної сфери та інших сфер.
Нечіткі множини широко використовуються в різних застосуваннях штучного інтелекту, теорії розпізнавання образів, теорії прийняття рішень тощо. Якщо до твердження «логічно кажучи, можна вивести майже всю сучасну математику з єдиного джерела – теорії множин» додати концепцію нечіткості, то це відкриє шлях до «подвоєння» математики: доповнюючи звичайну множину нечіткою (розпливчастою), можна кожному об’єкту в математиці поставити у відповідність його нечіткий (розпливчастий) аналог.
Означення 2.10. Нехай є множина  , елементи якої позначаються через
, елементи якої позначаються через  . Тоді нечіткою множиною
. Тоді нечіткою множиною  в множині
в множині  є сукупність упорядкованих пар
є сукупність упорядкованих пар  , де
, де 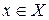 а
а  – ступінь належності елемента
– ступінь належності елемента  до нечіткої множини
до нечіткої множини  , тобто кожному елементу з множини
, тобто кожному елементу з множини  ставиться у відповідність число
ставиться у відповідність число  з деякої множини чисел
з деякої множини чисел  , де
, де  називається простором належності. Коли
називається простором належності. Коли  містить тільки дві точки 0 та 1, множина
містить тільки дві точки 0 та 1, множина  не є нечіткою, тому що, кожному елементу
не є нечіткою, тому що, кожному елементу 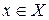 , який не належить нечіткій множині
, який не належить нечіткій множині  , відповідає ступінь належності
, відповідає ступінь належності  , кожному елементу
, кожному елементу 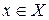 , який не належить нечіткій множині
, який не належить нечіткій множині  , відповідає ступінь належності
, відповідає ступінь належності  .
.
У теорії звичайних множин введено поняття характеристичного числа

Тобто характеристичне число  для всіх елементів
для всіх елементів  множини
множини  (
( )
)
Таким чином, ступінь належності в цьому випадку, повністю збігається з характеристичним числом. Тобто можна сказати, що якщо  , то елемент
, то елемент  абсолютно (на 100%) належить множині
абсолютно (на 100%) належить множині  , якщо
, якщо  , то елемент абсолютно (на 100%) не належить множині
, то елемент абсолютно (на 100%) не належить множині  . В цьому випадку
. В цьому випадку  теж є звичайною (чіткою) множиною, яка є підмножиною множини
теж є звичайною (чіткою) множиною, яка є підмножиною множини  , тобто деякі елементи множин
, тобто деякі елементи множин  належать множині
належать множині  , а деякі не належать. При цьому множина
, а деякі не належать. При цьому множина  містить два елемента: 1 і 0.
містить два елемента: 1 і 0.
В випадку з нечіткими множинами може бути й не 100-відсоткова належність елементів множини  до множини
до множини  . Тому у подальшому вважатимемо, що
. Тому у подальшому вважатимемо, що  є відрізком [0, 1], причому 0 й 1 є відповідно нижчим і вищим ступенями належності. Основне припущення полягає в тому, що нечітка множина
є відрізком [0, 1], причому 0 й 1 є відповідно нижчим і вищим ступенями належності. Основне припущення полягає в тому, що нечітка множина  може бути точно визначена зіставленням кожному об’єкту х числа, яке знаходиться в діапазоні від 0 до 1 і відображає ступінь його належності
може бути точно визначена зіставленням кожному об’єкту х числа, яке знаходиться в діапазоні від 0 до 1 і відображає ступінь його належності  .
.
У теорії нечітких множин так само, як і в теорії чітких множин, широко використовується поняття універсальної множини. При цьому універсальною множиною  нечіткої множини
нечіткої множини  називається область визначення функції належності
називається область визначення функції належності 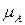 .
.
Нечітка множина  ,
, 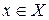 , визначається математично як сукупність упорядкованих пар, складених з елементів
, визначається математично як сукупність упорядкованих пар, складених з елементів  універсальної множини
універсальної множини  і відповідних ступенів належності
і відповідних ступенів належності  або безпосередньо у вигляді функції
або безпосередньо у вигляді функції
 .
.
У науковій літературі можливі такі записи нечітких множин:
 ;
;
 ;
;
 ,
,
або у вигляді табл.2.1.
| Таблиця 2.1 | ||||||||
| х | 
| 
| 
| 
| 
| 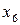
| 
| |

| 0,2 | 0,6 | 0,3 | 0,8 | ||||
Приклад 2.17. Щоб детальніше пояснити поняття нечіткої підмножини, розглянемо такий приклад. Передбачимо, що деяка множина  складається з дев’яти елементів
складається з дев’яти елементів 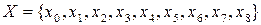 ,
,
 .
.
Отже, нечітка підмножина  : не містить
: не містить  і
і 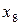 ; у невеликій мірі містить
; у невеликій мірі містить  ,
,  ; містить
; містить  трохи більше, ніж
трохи більше, ніж 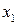 і
і 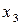 ; у значно більшій мірі містить
; у значно більшій мірі містить  і
і  , не повністю містить
, не повністю містить 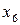 і
і  . Таким чином, можна створити математичну структуру, що дає змогу оперувати елементами.
. Таким чином, можна створити математичну структуру, що дає змогу оперувати елементами.
Як приклад можна розглядати множину  , де кожен елемент
, де кожен елемент  позначає зріст людини у сантиметрах, а саме
позначає зріст людини у сантиметрах, а саме  ,
,  ,
, 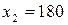 ,
, 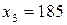 ,
, 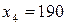 ,
,  ,
,  ,
, 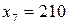 ,
,  . А множина
. А множина  описує таке нечітке поняття, як «бути дуже високою за зрістом людиною».
описує таке нечітке поняття, як «бути дуже високою за зрістом людиною».
Наведемо означення поняття нечіткої підмножини, введеного засновником теорії нечітких множин Л. Заде [3]: «Нечітка підмножина  універсальної множини
універсальної множини  характеризується функцією належності
характеризується функцією належності  , що ставить у відповідність кожному елементу
, що ставить у відповідність кожному елементу  число
число  із множини [0,1] і характеризує міру належності елемента
із множини [0,1] і характеризує міру належності елемента 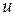 підмножині
підмножині  ».
».
Означення 2.11. Множина, що містить єдиний елемент, називається синглетоном.
Синглетон може визначатися як серед чітких, так і серед нечітких множин.
Означення 2.12. Носієм нечіткої множини  називається множина
називається множина  таких точок в
таких точок в  , для яких функція
, для яких функція  – додатна.
– додатна.
Для вище приведеного прикладу 2.17  .
.
Означення 2.13. Висотою нечіткої множини  називається величина
називається величина  .
.
Для вище приведеного прикладу  .
.
Означення 2.14. Точкою переходу нечіткої множини  називається такий елемент множини
називається такий елемент множини  , ступінь належності якого множині
, ступінь належності якого множині  дорівнює 0,5.
дорівнює 0,5.
Для вище приведеного прикладу точка переходу – це елемент  .
.






