4.Для проверки правильности решения составим сумму моментов относительно точки В:

Ответ:
Опорные реакции балки равны:
VA = кН;
HA = кН;
mA = кН.
ВАРИАНТ №11
Задача №1.
Определить реакции опор балки, нагруженной, как показано на рис.1.
Дано: а = 2м, b = 4м, с = 2м, d = 4м, e = 2м, q = 40кН/м, F1 = 80кН,
F2 = 40кН, m = 20кН·м, α = 450.
F1 q
m х
А α В
F2
a b c d e
Рис.1
Определить: реакции опор VА, НА, VВ.
Решение.
y
m VA F1 q VB
x
HA F2y F2x Fq1 Fq2
2 2 1 1
2 4 2 4 2
Рис. 2
1. Обозначаем опоры буквами А и В. Отбрасываем связи (опоры А и В), заменяем их действие реакциями: неподвижная опора имеет реакции VА (вертикальная) и НА (горизонтальная), подвижная опора – реакцию VВ (вертикальная). Выбираем систему координат XY с началом в левой опоре. Определяем равнодействующую распределенной нагрузки: равнодействующих будет две – одна на участке «d» (Fq1), другая на участке «e»(Fq2):

 e =
e =
и чертим расчетную схему балки (рис.2).
1. Для полученной плоской произвольной системы сил составляем уравнения равновесия:
 (1);
(1);
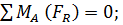

 (3).
(3).
2. Решаем систему уравнений. Из уравнения (1) находим НА:


Из уравнения (2) находим VB:

Из уравнения (3) находим VA:

3. Для проверки правильности решения составим сумму проекций на ось Y:

Ответ:
Опорные реакции балки равны:
VA = кН;
VB = кН;
HA = кН.
Задача №2.
Определить реакции опор балки, нагруженной, как показано на рис. 3.
Дано: а = 2м, b = 4м, с = 2м, q = 40кН/м, F1 = 80кН, F2 = 40кН,
m = 20кН·м, α = 450.
y
F2 q
x
А α m
F1
a b c
Рис.3
Определить: реакции опоры VА, НА, mА.
Решение.
y
VA F2 q
mA х
HA А F1x m
F1y Fq
1 1
2 4 2
Рис.4
1. Обозначаем опору буквой А. Отбрасываем связь (опору А), заменяем ее действие реакциями: жесткая заделка имеет реакции VА (вертикальная), НА (горизонтальная), mA(реактивный момент). Выбираем систему координат XY с началом в опоре. Определяем равнодействующую распределенной нагрузки:
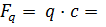
и чертим расчетную схему балки (рис.4).
2. Для полученной плоской произвольной системы сил составляем уравнения равновесия:
 (1)
(1)
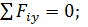 (2)
(2)
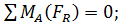 (3)
(3)
3 Решаем систему уравнений. Из уравнения (1) находим НА:

 Из уравнения (2) находим VA:
Из уравнения (2) находим VA:

Из уравнения (3) находим mA:
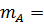
4.Для проверки правильности решения составим сумму моментов относительно точки В:

Ответ:
Опорные реакции балки равны:
VA = кН;
HA = кН;
mA = кН.
ВАРИАНТ №12
Задача №1.
Определить реакции опор балки, нагруженной, как показано на рис.1.
Дано: а = 2м, b = 3м, с = 2м, d = 6м, e = 1м, q = 30кН/м, F1 = 40кН,
F2 = 80кН, m = 10кН·м, α = 600.
F1 q
m
А α В
F2
a b c d e
Рис.1
Определить: реакции опор VА, НА, VВ.
Решение.
y
m VA F1 q VB
x
HA F2y F2x Fq1 Fq2
3 3 0,5 0,5
2 3 2 6 1
Рис. 2
1. Обозначаем опоры буквами А и В. Отбрасываем связи (опоры А и В), заменяем их действие реакциями: неподвижная опора имеет реакции VА (вертикальная) и НА (горизонтальная), подвижная опора – реакцию VВ (вертикальная). Выбираем систему координат XY с началом в левой опоре. Определяем равнодействующую распределенной нагрузки: равнодействующих будет две – одна на участке «d» (Fq1), другая на участке «e»(Fq2):

 e =
e =
и чертим расчетную схему балки (рис.2).
1. Для полученной плоской произвольной системы сил составляем уравнения равновесия:
 (1);
(1);
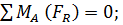

 (3).
(3).
2. Решаем систему уравнений. Из уравнения (1) находим НА:


Из уравнения (2) находим VB:

Из уравнения (3) находим VA:

3. Для проверки правильности решения составим сумму проекций на ось Y:

Ответ:
Опорные реакции балки равны:
VA = кН;
VB = кН;
HA = кН.
Задача №2.
Определить реакции опор балки, нагруженной, как показано на рис. 3.
Дано: а = 2м, b = 3м, с = 2м, q = 30кН/м, F1 = 40кН, F2 = 80кН,
m = 10кН·м, α = 600.
y
F2 q
x
А α m
F1
a b c
Рис.3
Определить: реакции опоры VА, НА, mА.
Решение.
y
VA F2 q
mA х
HA А F1x m
F1y Fq
1,0 1,0
2 3 2
Рис.4
1. Обозначаем опору буквой А. Отбрасываем связь (опору А), заменяем ее действие реакциями: жесткая заделка имеет реакции VА (вертикальная), НА (горизонтальная), mA(реактивный момент). Выбираем систему координат XY с началом в опоре. Определяем равнодействующую распределенной нагрузки:
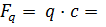
и чертим расчетную схему балки (рис.4).
2. Для полученной плоской произвольной системы сил составляем уравнения равновесия:
 (1)
(1)
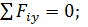 (2)
(2)
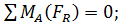 (3)
(3)
3 Решаем систему уравнений. Из уравнения (1) находим НА:

 Из уравнения (2) находим VA:
Из уравнения (2) находим VA:

Из уравнения (3) находим mA:
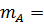
4.Для проверки правильности решения составим сумму моментов относительно точки В:

Ответ:
Опорные реакции балки равны:
VA = кН;
HA = кН;
mA = кН.
ВАРИАНТ №13
Задача №1.
Определить реакции опор балки, нагруженной, как показано на рис.1.
Дано: а = 1м, b = 4м, с = 1м, d = 5м, e = 2м, q = 10кН/м, F1 = 50кН,
F2 = 40кН, m = 20кН·м, α = 300.
F1 F2 q
m α
А В
a b c d e
Рис.1
Определить: реакции опор VА, НА, VВ.
Решение.
y
VA F1y F2 VB
x
m HA F1х Fq1 Fq2 Fq3
0,5 0,5 2,5 2,5 1 1
1 4 1 5 2
Рис. 2
1. Обозначаем опоры буквами А и В. Отбрасываем связи (опоры А и В), заменяем их действие реакциями: неподвижная опора имеет реакции VА (вертикальная) и НА (горизонтальная), подвижная опора – реакцию VВ (вертикальная). Выбираем систему координат XY с началом в левой опоре. Определяем равнодействующую распределенной нагрузки: равнодействующих будет три – одна на участке «с» (Fq1), другая на участке «d»(Fq2), третья на участке «е»(Fq3):
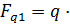 с =
с =
 d =
d =
 e =
e =
и чертим расчетную схему балки (рис.2).
1. Для полученной плоской произвольной системы сил составляем уравнения равновесия:
 (1);
(1);
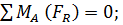 (2)
(2)
 (3).
(3).
2. Решаем систему уравнений. Из уравнения (1) находим НА:


Из уравнения (2) находим VB:

Из уравнения (3) находим VA:

3. Для проверки правильности решения составим сумму проекций на ось Y:
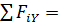
Ответ:
Опорные реакции балки равны:
VA = кН;
VB = кН;
HA = кН.
Задача №2.
Определить реакции опор балки, нагруженной, как показано на рис. 3.
Дано: а = 1м, b = 4м, с = 1м, q = 10кН/м, F1 = 50кН, F2 = 40кН,
m = 20кН·м, α = 300.
y
F1 F2 q
α x
А m
a b c
Рис.3
Определить: реакции опоры VА, НА, mА.
Решение.
y
VA F1y F2 q
mA m х
HA А F1x В
Fq
0,5 0,5
1 4 1
Рис.4
1. Обозначаем опору буквой А. Отбрасываем связь (опору А), заменяем ее действие реакциями: жесткая заделка имеет реакции VА (вертикальная), НА (горизонтальная), mA(реактивный момент). Выбираем систему координат XY с началом в опоре. Определяем равнодействующую распределенной нагрузки:

и чертим расчетную схему балки (рис.4).
2. Для полученной плоской произвольной системы сил составляем уравнения равновесия:
 (1)
(1)
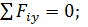 (2)
(2)
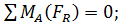 (3)
(3)
3 Решаем систему уравнений. Из уравнения (1) находим НА:

 Из уравнения (2) находим VA:
Из уравнения (2) находим VA:

Из уравнения (3) находим mA:
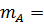
4.Для проверки правильности решения составим сумму моментов относительно точки В:

Ответ:
Опорные реакции балки равны:
VA = кН;
HA = кН;
mA = кН.
ВАРИАНТ №14
Задача №1.
Определить реакции опор балки, нагруженной, как показано на рис.1.
Дано: а = 1м, b = 5м, с = 1м, d = 4м, e = 1м, q = 40кН/м, F1 = 80кН,
F2 = 60кН, m = 10кН·м, α = 450.
F1 F2 q
m α
А В
a b c d e
Рис.1
Определить: реакции опор VА, НА, VВ.
Решение.
y
VA F1y F2 VB
m x
HA F1х Fq1 Fq2 Fq3
0,5 0,5 2 2 0,5 0,5
1 5 1 4 1
Рис. 2
1. Обозначаем опоры буквами А и В. Отбрасываем связи (опоры А и В), заменяем их действие реакциями: неподвижная опора имеет реакции VА (вертикальная) и НА (горизонтальная), подвижная опора – реакцию VВ (вертикальная). Выбираем систему координат XY с началом в левой опоре. Определяем равнодействующую распределенной нагрузки: равнодействующих будет три – одна на участке «с» (Fq1), другая на участке «d»(Fq2), третья на участке «е»(Fq3):
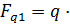 с =
с =
 d =
d =
 e =
e =
и чертим расчетную схему балки (рис.2).
1. Для полученной плоской произвольной системы сил составляем уравнения равновесия:
 (1);
(1);
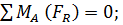 (2)
(2)
 (3).
(3).
2. Решаем систему уравнений. Из уравнения (1) находим НА:


Из уравнения (2) находим VB:

Из уравнения (3) находим VA:

3. Для проверки правильности решения составим сумму проекций на ось Y:
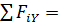
Ответ:
Опорные реакции балки равны:
VA = кН;
VB = кН;
HA = кН.
Задача №2.
Определить реакции опор балки, нагруженной, как показано на рис. 3.
Дано: а = 1м, b = 5м, с = 1м, q = 40кН/м, F1 = 80кН, F2 = 60кН,
m = 10кН·м, α = 450.
y
F1 F2 q
α x
А m
a b c
Рис.3
Определить: реакции опоры VА, НА, mА.
Решение.
y
VA F1y F2 q m
mA х
HA А F1x В
Fq
0,5 0,5
1 5 1
Рис.4
1. Обозначаем опору буквой А. Отбрасываем связь (опору А), заменяем ее действие реакциями: жесткая заделка имеет реакции VА (вертикальная), НА (горизонтальная), mA(реактивный момент). Выбираем систему координат XY с началом в опоре. Определяем равнодействующую распределенной нагрузки:
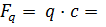
и чертим расчетную схему балки (рис.4).
2. Для полученной плоской произвольной системы сил составляем уравнения равновесия:
 (1)
(1)
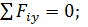 (2)
(2)
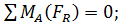 (3)
(3)
3 Решаем систему уравнений. Из уравнения (1) находим НА:

 Из уравнения (2) находим VA:
Из уравнения (2) находим VA:

Из уравнения (3) находим mA:
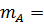
4.Для проверки правильности решения составим сумму моментов относительно точки В:

Ответ:
Опорные реакции балки равны:
VA = кН;
HA = кН;
mA = кН.
ВАРИАНТ №15
Задача №1.
Определить реакции опор балки, нагруженной, как показано на рис.1.
Дано: а = 1м, b = 6м, с = 1м, d = 3м, e = 2м, q = 20кН/м, F1 = 60кН,
F2 = 40кН, m = 10кН·м, α = 600.
F1 F2 q
m α
А В
a b c d e
Рис.1
Определить: реакции опор VА, НА, VВ.
Решение.
y
VA F1y F2 VB
x
m HA F1х Fq1 Fq2 Fq3
0,5 0,5 1,5 1,5 1 1
1 6 1 3 2
Рис. 2
1. Обозначаем опоры буквами А и В. Отбрасываем связи (опоры А и В), заменяем их действие реакциями: неподвижная опора имеет реакции VА (вертикальная) и НА (горизонтальная), подвижная опора – реакцию VВ (вертикальная). Выбираем систему координат XY с началом в левой опоре. Определяем равнодействующую распределенной нагрузки: равнодействующих будет три – одна на участке «с» (Fq1), другая на участке «d»(Fq2), третья на участке «е»(Fq3):
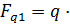 с =
с =
 d =
d =
 e =
e =
и чертим расчетную схему балки (рис.2).
1. Для полученной плоской произвольной системы сил составляем уравнения равновесия:
 (1);
(1);
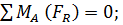 (2)
(2)
 (3).
(3).
2. Решаем систему уравнений. Из уравнения (1) находим НА:


Из уравнения (2) находим VB:

Из уравнения (3) находим VA:

3. Для проверки правильности решения составим сумму проекций на ось Y:
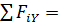
Ответ:
Опорные реакции балки равны:
VA = кН;
VB = кН;
HA = кН.
Задача №2.
Определить реакции опор балки, нагруженной, как показано на рис. 3.
Дано: а = 1м, b = 6м, с = 1м, q = 20кН/м, F1 = 60кН, F2 = 40кН,
m = 10кН·м, α = 600.
y
F1 F2 q
α x
А m
a b c
Рис.3
Определить: реакции опоры VА, НА, mА.
Решение.
y
VA F1y F2 q
mA m х
HA А F1x В
Fq
0,5 0,5
1 6 1
Рис.4
1. Обозначаем опору буквой А. Отбрасываем связь (опору А), заменяем ее действие реакциями: жесткая заделка имеет реакции VА (вертикальная), НА (горизонтальная), mA(реактивный момент). Выбираем систему координат XY с началом в опоре. Определяем равнодействующую распределенной нагрузки:
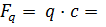
и чертим расчетную схему балки (рис.4).
2. Для полученной плоской произвольной системы сил составляем уравнения равновесия:
 (1)
(1)
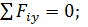 (2)
(2)
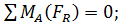 (3)
(3)
3 Решаем систему уравнений. Из уравнения (1) находим НА:

 Из уравнения (2) находим VA:
Из уравнения (2) находим VA:

Из уравнения (3) находим mA:
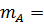
4.Для проверки правильности решения составим сумму моментов относительно точки В:

Ответ:
Опорные реакции балки равны:
VA = кН;
HA = кН;
mA = кН.
ВАРИАНТ №16
Задача №1.
Определить реакции опор балки, нагруженной, как показано на рис.1.
Дано: а = 2м, b = 4м, с = 1м, d = 4м, e = 2м, q = 40кН/м, F1 = 60кН,
F2 = 80кН, m = 20кН·м, α = 600.
F1 F2 q
m α
А В
a b c d e
Рис.1
Определить: реакции опор VА, НА, VВ.
Решение.
y
VA F1y F2 VB
m x
HA F1х Fq1 Fq2 Fq3
0,5 0,5 2 2 1 1
2 4 1 4 2
Рис. 2
1. Обозначаем опоры буквами А и В. Отбрасываем связи (опоры А и В), заменяем их действие реакциями: неподвижная опора имеет реакции VА (вертикальная) и НА (горизонтальная), подвижная опора – реакцию VВ (вертикальная). Выбираем систему координат XY с началом в левой опоре. Определяем равнодействующую распределенной нагрузки: равнодействующих будет три – одна на участке «с» (Fq1), другая на участке «d»(Fq2), третья на участке «е»(Fq3):
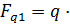 с =
с =
 d =
d =
 e =
e =
и чертим расчетную схему балки (рис.2).
1. Для полученной плоской произвольной системы сил составляем уравнения равновесия:
 (1);
(1);
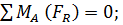 (2)
(2)






