Окончательно получим:
N1 = кН,
N2 = кН.
Ответ:
Аналитическое решение: N1 = кН
N2 = кН.
Графическое решение: N1 = кН
N2 = кН.
ВАРИАНТ №13
Задача №1.
Определить равнодействующую сходящихся сил аналитическим и графическим методами (рис 1).
y F1 Дано:
F1 = 65 кН, F2 = 75 кН,
F3 = 55 кН, α1 = 140 о,
α1 F2 x α2 = 20 о.
α2 Определить: R.
F3
Рис.1
Решение.
1. Аналитический метод.
Сначала надо определить проекции заданных сил на оси координат, после чего легко найти проекцию равнодействующей силы на эти оси.
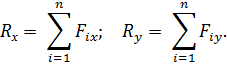
Величину равнодействующей найдем по формуле
Строим схему с соблюдением заданных углов α1 и α2 (без соблюдения масштаба сил, рис 2).
y
x
Рис.2
Для вычисления проекций сил сначала определяем знак проекции, а затем ее абсолютную величину. Проекция положительна, если угол между положительным направлением оси и силой меньше 900 (сила и ось направлены в одну сторону); в противном случае проекция отрицательна. Чтобы получить величину проекции, надо умножить величину силы на косинус угла между силой и ее проекцией (т.е. всегда берется косинус острого угла).
Проекция равнодействующей силы:
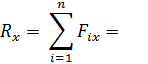
ее величина
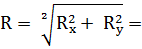
2.Графический метод.
Выберем масштаб сил: m = 10кН/см, тогда силы F1, F2, F3 будут откладываться отрезками:
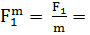
Рис.3
R = см
R = · m = ·10 = кН.
Задача №2.
Определить усилия в стержнях АС и АВ, возникающие от силы F, приложенной к узлу А, аналитическим и графическим методами (рис.4).
F Дано: F = 35кН.
B
30о
23о A
80о
C
Рис.4
Определить: усилия NАВ и NАС.
Решение:
F F
B N1
1 30oA 30o A
80o 2 23o
CN2
Рис.5 Рис.6
1. Строим схему, соблюдая все заданные углы (без соблюдения масштаба сил, рис.5). Рассматриваем равновесие точки А, в которой сходятся все стержни и внешние силы.
2. Отбрасываем связи АВ и АС, заменяя их усилиями в стержнях N1 и N2. Направление усилий примем от узла А, предполагая стержни растянутыми. Выполним на отдельном чертеже схему действия сил в точке А (рис.6).
3. Выберем систему координат таким образом, чтобы одна из осей совпала с неизвестным усилием. Составляем уравнения равновесия плоской системы сходящихся сил:
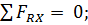(1)
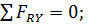(2)
Из уравнения () находим усилие 
:
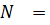
Найденное значение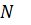 
подставляем в уравнение () и находим из него значение :
Окончательно получаем:
N1 =
N2 =
II. Графический метод.
1. Так как узел А находится в равновесии, то многоугольник из заданной и двух искомых сил должен быть замкнутым. Выбираем масштаб сил m = 10кН/см, тогда сила F будут откладываться отрезком:
Из произвольной т.О откладываем отрезок, соответствующий величине и направлению силы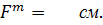 
Силы N1 и N2 неизвестны, но известны их направления. Поэтому, зная, что силовой многоугольник должен быть замкнут (условие равновесия сходящихся сил), из начала отрезка F проводим прямую, параллельную вектору , а из конца отрезка F проводим прямую, параллельную вектору . Точка их пересечения является вершиной силового многоугольника (рис 7). Стрелки у искомых векторов ставим так, чтобы они шли в одном направлении со стрелками заданных векторов. Получим замкнутый силовой многоугольник.
Рис.7
N1= см; N2 = см.
Измерив отрезки и, умножая их на масштаб, получим:
N1= · 10 = кН;
N2 = · 10 = кН.
Остается выяснить, растянуты или сжаты стержни N1 и N2. Для этого нужно сравнить их направление в многоугольнике сил с направлениями, что мы предположили в начале. Если направления совпадают, то стержень растянут, если направления не совпадают, то стержень сжат.
Окончательно получим:
N1 = кН,
N2 = кН.
Ответ:
Аналитическое решение: N1 = кН
N2 = кН.
Графическое решение: N1 = кН
N2 = кН.
ВАРИАНТ №14
Задача №1.
Определить равнодействующую сходящихся сил аналитическим и графическим методами (рис 1).
y F1 Дано:
F1 = 75 кН, F2 = 65 кН,
F3 = 75 кН, α1 = 20 о,
α1 F2 x α2 = 140 о.
α2 Определить: R.
F3
Рис.1
Решение.
1. Аналитический метод.
Сначала надо определить проекции заданных сил на оси координат, после чего легко найти проекцию равнодействующей силы на эти оси.
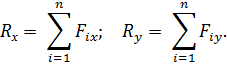
Величину равнодействующей найдем по формуле
Строим схему с соблюдением заданных углов α1 и α2 (без соблюдения масштаба сил, рис 2).
y
x
Рис.2
Для вычисления проекций сил сначала определяем знак проекции, а затем ее абсолютную величину. Проекция положительна, если угол между положительным направлением оси и силой меньше 900 (сила и ось направлены в одну сторону); в противном случае проекция отрицательна. Чтобы получить величину проекции, надо умножить величину силы на косинус угла между силой и ее проекцией (т.е. всегда берется косинус острого угла).
Проекция равнодействующей силы:
ее величина
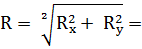
2.Графический метод.
Выберем масштаб сил: m = 10кН/см, тогда силы F1, F2, F3 будут откладываться отрезками:
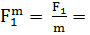
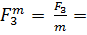
Рис.3
R = см
R = · m = ·10 = кН.
Задача №2.
Определить усилия в стержнях АС и АВ, возникающие от силы F, приложенной к узлу А, аналитическим и графическим методами (рис.4).
F Дано: F = 45 кН.
B
30о
23о A
80о
C
Рис.4
Определить: усилия NАВ и NАС.
Решение:
F F
B N1
130oA 30o A
80o 2 23o
C N2
Рис.5 Рис.6
1. Строим схему, соблюдая все заданные углы (без соблюдения масштаба сил, рис.5). Рассматриваем равновесие точки А, в которой сходятся все стержни и внешние силы.
2. Отбрасываем связи АВ и АС, заменяя их усилиями в стержнях N1 и N2. Направление усилий примем от узла А, предполагая стержни растянутыми. Выполним на отдельном чертеже схему действия сил в точке А (рис.6).
3. Выберем систему координат таким образом, чтобы одна из осей совпала с неизвестным усилием. Составляем уравнения равновесия плоской системы сходящихся сил:
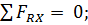(1)
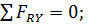(2)
Из уравнения () находим усилие :
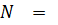
Найденное значение 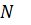подставляем в уравнение () и находим из него значение :
Окончательно получаем:
N1 =
N2 =
II. Графический метод.
1. Так как узел А находится в равновесии, то многоугольник из заданной и двух искомых сил должен быть замкнутым. Выбираем масштаб сил m = 10кН/см, тогда сила F будут откладываться отрезком:
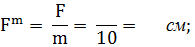
Из произвольной т.О откладываем отрезок, соответствующий величине и направлению силы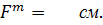
Силы N1 и N2 неизвестны, но известны их направления. Поэтому, зная, что силовой многоугольник должен быть замкнут (условие равновесия сходящихся сил), из начала отрезка F проводим прямую, параллельную вектору , а из конца отрезка F проводим прямую, параллельную вектору . Точка их пересечения является вершиной силового многоугольника (рис 7). Стрелки у искомых векторов ставим так, чтобы они шли в одном направлении со стрелками заданных векторов. Получим замкнутый силовой многоугольник.
Рис.7
N1 = см; N2 = см.
Измерив отрезки и, умножая их на масштаб, получим:
N1= · 10 = кН;
N2 = · 10 = кН.
Остается выяснить, растянуты или сжаты стержни NАВ и NАС. Для этого нужно сравнить их направление в многоугольнике сил с направлениями, что мы предположили в начале. Если направления совпадают, то стержень растянут, если направления не совпадают, то стержень сжат.
Окончательно получим:
N1 = кН,
N2 = кН.
Ответ:
Аналитическое решение: N1 = кН
N2 = кН.
Графическое решение: N1 = кН
N2 = кН.
ВАРИАНТ №15
Задача №1.
Определить равнодействующую сходящихся сил аналитическим и графическим методами (рис 1).
y F1 Дано:
F1 = 55 кН, F2 = 55 кН,
F3 = 65 кН, α1 = 30 о,
α1 F2 x α2 = 110 о.
α2 Определить: R.
F3
Рис.1
Решение.
1. Аналитический метод.
Сначала надо определить проекции заданных сил на оси координат, после чего легко найти проекцию равнодействующей силы на эти оси.
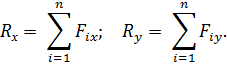
Величину равнодействующей найдем по формуле
Строим схему с соблюдением заданных углов α1 и α2 (без соблюдения масштаба сил, рис 2).
y
x
Рис.2
Для вычисления проекций сил сначала определяем знак проекции, а затем ее абсолютную величину. Проекция положительна, если угол между положительным направлением оси и силой меньше 900 (сила и ось направлены в одну сторону); в противном случае проекция отрицательна. Чтобы получить величину проекции, надо умножить величину силы на косинус угла между силой и ее проекцией (т.е. всегда берется косинус острого угла).
Проекция равнодействующей силы:
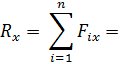
ее величина
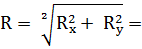
2.Графический метод.
Выберем масштаб сил: m = 10кН/см, тогда силы F1, F2, F3 будут откладываться отрезками:
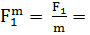
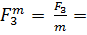
Рис.3
R = см
R = · m = ·10 = кН.
Задача №2.
Определить усилия в стержнях АС и АВ, возникающие от силы F, приложенной к узлу А, аналитическим и графическим методами (рис.4).
F Дано: F = 55 кН.
B
30о
23о A
80о
C
Рис.4
Определить: усилия NАВ и NАС.
Решение:
F F
B N1
130oA 30o A
80o 2 23o
C N2
Рис.5 Рис.6
1. Строим схему, соблюдая все заданные углы (без соблюдения масштаба сил, рис.5). Рассматриваем равновесие точки А, в которой сходятся все стержни и внешние силы.
2. Отбрасываем связи АВ и АС, заменяя их усилиями в стержнях N1 и N2. Направление усилий примем от узла А, предполагая стержни растянутыми. Выполним на отдельном чертеже схему действия сил в точке А (рис.6).
3. Выберем систему координат таким образом, чтобы одна из осей совпала с неизвестным усилием. Составляем уравнения равновесия плоской системы сходящихся сил:
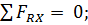(1)
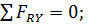(2)
Из уравнения () находим усилие :
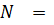
Найденное значение 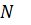подставляем в уравнение () и находим из него значение :
Окончательно получаем:
N1 =
N2 =
II. Графический метод.
1. Так как узел А находится в равновесии, то многоугольник из заданной и двух искомых сил должен быть замкнутым. Выбираем масштаб сил m = 10кН/см, тогда сила F будут откладываться отрезком:
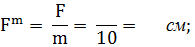
Из произвольной т.О откладываем отрезок, соответствующий величине и направлению силы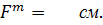
Силы N1 и N2 неизвестны, но известны их направления. Поэтому, зная, что силовой многоугольник должен быть замкнут (условие равновесия сходящихся сил), из начала отрезка F проводим прямую, параллельную вектору , а из конца отрезка F проводим прямую, параллельную вектору . Точка их пересечения является вершиной силового многоугольника (рис 7). Стрелки у искомых векторов ставим так, чтобы они шли в одном направлении со стрелками заданных векторов. Получим замкнутый силовой многоугольник.
Рис.7
N1 = см; N2 = см.
Измерив отрезки и, умножая их на масштаб, получим:
N1= · 10 = кН;
N2 = · 10 = кН.
Остается выяснить, растянуты или сжаты стержни N1 и N2. Для этого нужно сравнить их направление в многоугольнике сил с направлениями, что мы предположили в начале. Если направления совпадают, то стержень растянут, если направления не совпадают, то стержень сжат.
Окончательно получим:
N1= кН,
N2 = кН.
Ответ:
Аналитическое решение: N1 = кН
N2 = кН.
Графическое решение: N1 = кН
N2 = кН.
ВАРИАНТ №16
Задача №1.
Определить равнодействующую сходящихся сил аналитическим и графическим методами (рис 1).
y F1 Дано:
F1 = 20 кН, F2 = 40 кН,
F3 = 20 кН, α1 = 20 о,
α1 F2 x α2 = 65 о.
α2 Определить: R.
F3
Рис.1
Решение.
1. Аналитический метод.
Сначала надо определить проекции заданных сил на оси координат, после чего легко найти проекцию равнодействующей силы на эти оси.
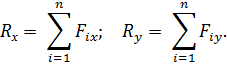
Величину равнодействующей найдем по формуле
Строим схему с соблюдением заданных углов α1 и α2 (без соблюдения масштаба сил, рис 2).
y
x
Рис.2
Для вычисления проекций сил сначала определяем знак проекции, а затем ее абсолютную величину. Проекция положительна, если угол между положительным направлением оси и силой меньше 900 (сила и ось направлены в одну сторону); в противном случае проекция отрицательна. Чтобы получить величину проекции, надо умножить величину силы на косинус угла между силой и ее проекцией (т.е. всегда берется косинус острого угла).
Проекция равнодействующей силы:
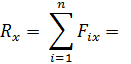
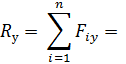
ее величина
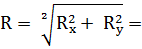
2.Графический метод.
Выберем масштаб сил: m = 10кН/см, тогда силы F1, F2, F3 будут откладываться отрезками:
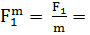
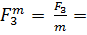
Рис.3
R = см
R = · m = ·10 = кН.
Задача №2.
Определить усилия в стержнях АС и АВ, возникающие от силы F, приложенной к узлу А, аналитическим и графическим методами (рис.4).
Дано: F = 25 кН.
A F
90o
B 90o 40o C
Рис.4
Определить: усилия NАВ и NАС.
Решение:
A F A F
90o
1 2 500N2
B 90o 40o C N1
Рис.5 Рис.6
1. Строим схему, соблюдая все заданные углы (без соблюдения масштаба сил, рис.5). Рассматриваем равновесие точки А, в которой сходятся все стержни и внешние силы.
2. Отбрасываем связи АВ и АС, заменяя их усилиями в стержнях N1 и N2. Направление усилий примем от узла А, предполагая стержни растянутыми. Выполним на отдельном чертеже схему действия сил в точке А (рис.6).
3. Выберем систему координат таким образом, чтобы одна из осей совпала с неизвестным усилием. Составляем уравнения равновесия плоской системы сходящихся сил:
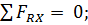(1)
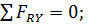(2)
Из уравнения () находим усилие :
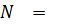
Найденное значение 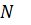подставляем в уравнение () и находим из него значение :
Окончательно получаем:
N1 =
N2 =
II. Графический метод.
1. Так как узел А находится в равновесии, то многоугольник из заданной и двух искомых сил должен быть замкнутым. Выбираем масштаб сил m = 10кН/см, тогда сила F будут откладываться отрезком:
Из произвольной т.О откладываем отрезок, соответствующий величине и направлению силы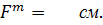
Силы N1 и N2 неизвестны, но известны их направления. Поэтому, зная, что силовой многоугольник должен быть замкнут (условие равновесия сходящихся сил), из начала отрезка F проводим прямую, параллельную вектору , а из конца отрезка F проводим прямую, параллельную вектору . Точка их пересечения является вершиной силового многоугольника (рис 7). Стрелки у искомых векторов ставим так, чтобы они шли в одном направлении со стрелками заданных векторов. Получим замкнутый силовой многоугольник.
Рис.7
N1 = см; N2 = см.
Измерив отрезки и, умножая их на масштаб, получим:
N1= · 10 = кН;
N2 = · 10 = кН.
Остается выяснить, растянуты или сжаты стержни N1 и N2. Для этого нужно сравнить их направление в многоугольнике сил с направлениями, что мы предположили в начале. Если направления совпадают, то стержень растянут, если направления не совпадают, то стержень сжат.
Окончательно получим:
N1 = кН,
N2 = кН.
Ответ:
Аналитическое решение: N1= кН
N2 = кН.
Графическое решение: N1 = кН
N2 = кН.
ВАРИАНТ №17
Задача №1.
Определить равнодействующую сходящихся сил аналитическим и графическим методами (рис 1).
y F1 Дано:
F1 = 30 кН, F2 = 30 кН,
F3 = 30 кН, α1 = 65 о,
α1 F2 x α2 = 20 о.
α2 Определить: R.
F3
Рис.1
Решение.
1. Аналитический метод.
Сначала надо определить проекции заданных сил на оси координат, после чего легко найти проекцию равнодействующей силы на эти оси.
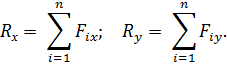
Величину равнодействующей найдем по формуле
Строим схему с соблюдением заданных углов α1 и α2 (без соблюдения масштаба сил, рис 2).
