МИНИСТЕРСТВО ОБРАЗОВАНИЯ САРАТОВСКОЙ ОБЛАСТИ
государственное автономное профессиональное образовательное учреждение
Саратовской области
«Саратовский архитектурно-строительный колледж»
УТВЕРЖДАЮ
Зам. директора по учебной работе
______________ Муравьёва О.И.
«____»____________2012 г
Рабочая тетрадь по выполнению
Расчётно-графической работы №1
дисциплина «Техническая механика»
для студентов дневного отделения специальностей:
08.02.01 Строительство и эксплуатация зданий и сооружений
углублённой подготовки
08.02.01 Строительство и эксплуатация зданий и сооружений
базовой подготовки
08.02.07 Монтаж и эксплуатация внутренних сантехнических устройств, кондиционирования воздуха и вентиляции базовой подготовки
07.02.01 Архитектура базовой подготовки
08.02.04 Водоснабжение и водоотведение базовой подготовки
08.02.08 Монтаж и эксплуатация оборудования и систем газоснабжения
базовой подготовки
Саратов 2012
Рассмотрено Одобрено методическим Советом
на заседании предметной ГБОУ СО СПО САСК
(цикловой) комиссии
архитектурно-строительного цикла Протокол №________________
______________________________ «_____»_______________2012г
Председатель ПК
___________________/Князева Е.Н./ Председатель______________
Разработал
преподаватель: Митрякова Н.Б.
Содержание
1. Цель работы…………..…………………………………………………………… 3
2. РГР №1.Вариант №1 ………………………………………………………..….… 5
3. Вариант №2 …………………………………………………………………….. 12
4. Вариант №3 …………………………………………………………………….. 19
5. Вариант №4 …………………………………………………………………….26
6. Вариант №5 …………………………………………………………………...... 33
7. Вариант №.6 ……………………………………………………………………. 40
8. Вариант №.7…………………………………………………………………..… 47
9. Вариант №8 …………………………………………………………………….. 54
10. Вариант №9 ………………………………………………………………….….. 61
11. Вариант №10 ……………………………………………………………….…… 68
12. Вариант №11 ……………………………………………………………………. 75
13. Вариант №12 ……………………………………………………………………. 82
14. Вариант №13 ……………………………………………………………………..89
15. Вариант №14 …………………………………………………………………… 96
16. Вариант №15 ………………………………………………………………… 103
17. Вариант №16 …………………………………………………………………... 110
18. Вариант №17 ………………………………………………………………….. 117
19. Вариант №18 …………………………………………………………………... 124
20. Вариант №19 …………………………………………………………………… 131
21. Вариант №20 …………………………………………………………………... 138
22. Вариант №21 ……………………………………………………………………145
23. Вариант №22 ……………………………………………………………………152
24. Вариант №23 …………………………………………………………………... 159
25. Вариант №24 …………………………………………………………………. 166
26. Вариант №25 ………………………………………………………………….. 173
27. Вариант №26 ………………………………………………………………….. 180
28. Вариант №27 ………………………………………………………………….. 187
29. Вариант №28 …………………………………………………………..………..194
30. Вариант №29 ………………………………………………………………….. 201
31. Вариант №30 …………………………………………………………………...208
32. Приложение №1 (для специальности 08.02.01) ……………………….…….. 215
33. Приложение №2 (для специальности 08.02.04)…………………….………...216
34. Приложение №3 (для специальности 08.02.07) ……………………………… 217
35. Приложение №4 (для специальности 270801) ……………………………… 218
36. Приложение №5 (для специальности 270841) ……………………………….. 219
Цель работы
Современные тенденции в системе образования требуют сложившиеся традиционные методики обучения дополнять компьютерными технологиями. Они придают процессу обучения более эффективный и привлекательный характер.
Компьютеризация учебного процесса носит всеобъемлющий, комплексный характер и внедряется в лекционные и практические занятия, в самостоятельную работу студента.
Основной задачей практических занятий является развитие навыков решения задач, предлагаемых к самостоятельному решению в ходе выполнения расчетно-графических работ.
После прослушивания лекционного материала, проработки методики решения задач на практических занятиях, студентам предлагается произвести выполнение работы в электронном варианте. Для этого студент выбирает свой вариант, соответствующий его номеру по списку в журнале, и приступает к его решению. Порядок решения задач, методические рекомендации и примеры решения приведены в «Методических указаниях по выполнению расчетно-графических работ для студентов дневного отделения по дисциплине «Техническая механика».
По окончанию работы студент обязан сдать РГР в электронном варианте.
РГР №1.
ВАРИАНТ №1
Задача №1.
Определить равнодействующую сходящихся сил аналитическим и графическим методами (рис 1).
y F1 Дано:
F1 = 20 кН, F2 = 30 кН,
F3 = 40 кН, α1 = 40 о,
α1 F2 x α2 = 60 о.
α2 Определить: R.
F3
Рис.1
Решение.
1. Аналитический метод.
Сначала надо определить проекции заданных сил на оси координат, после чего легко найти проекцию равнодействующей силы на эти оси.
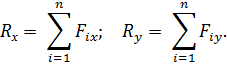
Величину равнодействующей найдем по формуле
Строим схему с соблюдением заданных углов α1 и α2 (без соблюдения масштаба сил, рис 2).
y
x
Рис.2
Для вычисления проекций сил сначала определяем знак проекции, а затем ее абсолютную величину. Проекция положительна, если угол между положительным направлением оси и силой меньше 900 (сила и ось направлены в одну сторону); в противном случае проекция отрицательна. Чтобы получить величину проекции, надо умножить величину силы на косинус угла между силой и ее проекцией (т.е. всегда берется косинус острого угла).
Проекция равнодействующей силы:
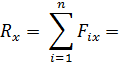
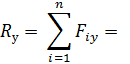
ее величина
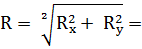
2.Графический метод.
Выберем масштаб сил: m = 10кН/см, тогда силы F1, F2, F3 будут откладываться отрезками:
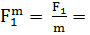
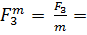
Рис.3
R = см
R = · m = ·10 = кН.
Задача №2.
Определить усилия в стержнях АС и АВ, возникающие от силы F, приложенной к узлу А, аналитическим и графическим методами (рис.4).
Дано: F = 40 кН.
А С
90o
F
В 40o
Рис.4
Определить: усилия NАВ и NАС.
Решение:
А 1 С А 400 N1
2 90о
В 40 N2
F F
Рис.5 Рис.6
1. Строим схему, соблюдая все заданные углы (без соблюдения масштаба сил, рис.5). Рассматриваем равновесие точки А, в которой сходятся все стержни и внешние силы.
2. Отбрасываем связи АВ и АС, заменяя их усилиями в стержнях N1 и N2. Направление усилий примем от узла А, предполагая стержни растянутыми. Выполним на отдельном чертеже схему действия сил в точке А (рис.6).
3. Выберем систему координат таким образом, чтобы одна из осей совпала с неизвестным усилием. Составляем уравнения равновесия плоской системы сходящихся сил:
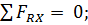(1)
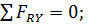(2)
Из уравнения () находим усилие 
:
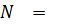
Найденное значение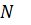 
подставляем в уравнение () и находим из него значение :
Окончательно получаем:
N1 =
N2 =
II. Графический метод.
1. Так как узел А находится в равновесии, то многоугольник из заданной и двух искомых сил должен быть замкнутым. Выбираем масштаб сил m = 10кН/см, тогда сила F будут откладываться отрезком:
Из произвольной т.О откладываем отрезок, соответствующий величине и направлению силы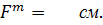 
Силы N1 и N2 неизвестны, но известны их направления. Поэтому, зная, что силовой многоугольник должен быть замкнут (условие равновесия сходящихся сил), из начала отрезка F проводим прямую, параллельную вектору , а из конца отрезка F проводим прямую, параллельную вектору . Точка их пересечения является вершиной силового многоугольника (рис 7). Стрелки у искомых векторов ставим так, чтобы они шли в одном направлении со стрелками заданных векторов. Получим замкнутый силовой многоугольник.
Рис.7
N1 = см; N2 = см.
Измерив отрезки и, умножая их на масштаб, получим:
N1= · 10 = кН;
N2 = · 10 = кН.
Остается выяснить, растянуты или сжаты стержни N1 и N2. Для этого нужно сравнить их направление в многоугольнике сил с направлениями, что мы предположили в начале. Если направления совпадают, то стержень растянут, если направления не совпадают, то стержень сжат.
Окончательно получим:
N1 = кН,
N2 = кН.
Ответ:
Аналитическое решение: N1 = кН
N2 = кН.
Графическое решение: N1 = кН
N2 = кН.
ВАРИАНТ №2
Задача №1.
Определить равнодействующую сходящихся сил аналитическим и графическим методами (рис 1).
y F1 Дано:
F1 = 40 кН, F2 = 20 кН,
F3 = 30 кН, α1 = 20 о,
α1 F2 x α2 = 40 о.
α2 Определить: R.
F3
Рис.1
Решение.
1. Аналитический метод.
Сначала надо определить проекции заданных сил на оси координат, после чего легко найти проекцию равнодействующей силы на эти оси.
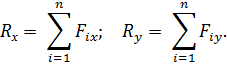
Величину равнодействующей найдем по формуле
Строим схему с соблюдением заданных углов α1 и α2 (без соблюдения масштаба сил, рис 2).
y
x
Рис.2
Для вычисления проекций сил сначала определяем знак проекции, а затем ее абсолютную величину. Проекция положительна, если угол между положительным направлением оси и силой меньше 900 (сила и ось направлены в одну сторону); в противном случае проекция отрицательна. Чтобы получить величину проекции, надо умножить величину силы на косинус угла между силой и ее проекцией (т.е. всегда берется косинус острого угла).
Проекция равнодействующей силы:
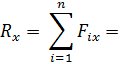
ее величина
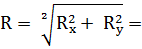
2.Графический метод.
Выберем масштаб сил: m = 10кН/см, тогда силы F1, F2, F3 будут откладываться отрезками:
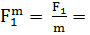
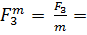
Рис.3
R = см
R = · m = ·10 = кН.
Задача №2.
Определить усилия в стержнях АС и АВ, возникающие от силы F, приложенной к узлу А, аналитическим и графическим методами (рис.4).
Дано: F = 50 кН.
А С
90o
F
В 40o
Рис.4
Определить: усилия NАВ и NАС.
Решение:
А 1 С А 400 N1
2 90о
В 40 N2
F F
Рис.5 Рис.6
1. Строим схему, соблюдая все заданные углы (без соблюдения масштаба сил, рис.5). Рассматриваем равновесие точки А, в которой сходятся все стержни и внешние силы.
2. Отбрасываем связи АВ и АС, заменяя их усилиями в стержнях N1 и N2. Направление усилий примем от узла А, предполагая стержни растянутыми. Выполним на отдельном чертеже схему действия сил в точке А (рис.6).
3. Выберем систему координат таким образом, чтобы одна из осей совпала с неизвестным усилием. Составляем уравнения равновесия плоской системы сходящихся сил:
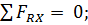(1)
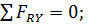(2)
Из уравнения () находим усилие :
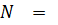
Найденное значение 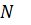подставляем в уравнение () и находим из него значение :
Окончательно получаем:
N1 =
N2 =
II. Графический метод.
1. Так как узел А находится в равновесии, то многоугольник из заданной и двух искомых сил должен быть замкнутым. Выбираем масштаб сил m = 10кН/см, тогда сила F будут откладываться отрезком:
Из произвольной т.О откладываем отрезок, соответствующий величине и направлению силы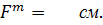
Силы N1 и N2 неизвестны, но известны их направления. Поэтому, зная, что силовой многоугольник должен быть замкнут (условие равновесия сходящихся сил), из начала отрезка F проводим прямую, параллельную вектору , а из конца отрезка F проводим прямую, параллельную вектору . Точка их пересечения является вершиной силового многоугольника (рис 7). Стрелки у искомых векторов ставим так, чтобы они шли в одном направлении со стрелками заданных векторов. Получим замкнутый силовой многоугольник.
Рис.7
N1= см; N2 = см.
Измерив отрезки и, умножая их на масштаб, получим:
N1= · 10 = кН;
N2 = · 10 = кН.
Остается выяснить, растянуты или сжаты стержни N1 и N2. Для этого нужно сравнить их направление в многоугольнике сил с направлениями, что мы предположили в начале. Если направления совпадают, то стержень растянут, если направления не совпадают, то стержень сжат.
Окончательно получим:
N1 = кН,
N2 = кН.
Ответ:
Аналитическое решение: N1 = кН
N2 = кН.
Графическое решение: N1 = кН
N2 = кН.
ВАРИАНТ №3
Задача №1.
Определить равнодействующую сходящихся сил аналитическим и графическим методами (рис 1).
y F1 Дано:
F1 = 20 кН, F2 = 40 кН,
F3 = 50 кН, α1 = 60 о,
α1 F2 x α2 = 110 о.
α2 Определить: R.
F3
Рис.1
Решение.
1. Аналитический метод.
Сначала надо определить проекции заданных сил на оси координат, после чего легко найти проекцию равнодействующей силы на эти оси.
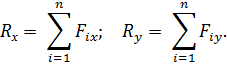
Величину равнодействующей найдем по формуле
Строим схему с соблюдением заданных углов α1 и α2 (без соблюдения масштаба сил, рис 2).
y
x
Рис.2
Для вычисления проекций сил сначала определяем знак проекции, а затем ее абсолютную величину. Проекция положительна, если угол между положительным направлением оси и силой меньше 900 (сила и ось направлены в одну сторону); в противном случае проекция отрицательна. Чтобы получить величину проекции, надо умножить величину силы на косинус угла между силой и ее проекцией (т.е. всегда берется косинус острого угла).
Проекция равнодействующей силы:
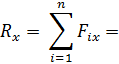
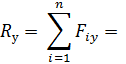
ее величина
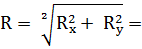
2.Графический метод.
Выберем масштаб сил: m = 10кН/см, тогда силы F1, F2, F3 будут откладываться отрезками:
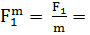
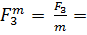
Рис.3
R = см
R = · m = ·10 = кН.
Задача №2.
Определить усилия в стержнях АС и АВ, возникающие от силы F, приложенной к узлу А, аналитическим и графическим методами (рис.4).
Дано: F = 60 кН.
А С
90o
F
В 40o
Рис.4
Определить: усилия NАВ и NАС.
Решение:
А 1 С А 400 N1
2 90о
В 40 N2
F F
Рис.5 Рис.6
1. Строим схему, соблюдая все заданные углы (без соблюдения масштаба сил, рис.5). Рассматриваем равновесие точки А, в которой сходятся все стержни и внешние силы.
2. Отбрасываем связи АВ и АС, заменяя их усилиями в стержнях N1 и N2. Направление усилий примем от узла А, предполагая стержни растянутыми. Выполним на отдельном чертеже схему действия сил в точке А (рис.6).
3. Выберем систему координат таким образом, чтобы одна из осей совпала с неизвестным усилием. Составляем уравнения равновесия плоской системы сходящихся сил:
(1)
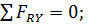(2)
Из уравнения () находим усилие :
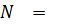
Найденное значение 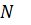подставляем в уравнение () и находим из него значение :
Окончательно получаем:
N1 =
N2 =
II. Графический метод.
1. Так как узел А находится в равновесии, то многоугольник из заданной и двух искомых сил должен быть замкнутым. Выбираем масштаб сил m = 10кН/см, тогда сила F будут откладываться отрезком:
Из произвольной т.О откладываем отрезок, соответствующий величине и направлению силы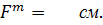
Силы N1 и N2 неизвестны, но известны их направления. Поэтому, зная, что силовой многоугольник должен быть замкнут (условие равновесия сходящихся сил), из начала отрезка F проводим прямую, параллельную вектору , а из конца отрезка F проводим прямую, параллельную вектору . Точка их пересечения является вершиной силового многоугольника (рис 7). Стрелки у искомых векторов ставим так, чтобы они шли в одном направлении со стрелками заданных векторов. Получим замкнутый силовой многоугольник.
Рис.7
N1= см; N2 = см.
Измерив отрезки и, умножая их на масштаб, получим:
N1= · 10 = кН;
N2 = · 10 = кН.
Остается выяснить, растянуты или сжаты стержни N1 и N2. Для этого нужно сравнить их направление в многоугольнике сил с направлениями, что мы предположили в начале. Если направления совпадают, то стержень растянут, если направления не совпадают, то стержень сжат.
Окончательно получим:
N1 = кН,
N2 = кН.
Ответ:
Аналитическое решение: N1 = кН
N2 = кН.
Графическое решение: N1 = кН
N2 = кН.
ВАРИАНТ №4
Задача №1.
Определить равнодействующую сходящихся сил аналитическим и графическим методами (рис 1).
y F1 Дано:
F1 = 30 кН, F2 = 50 кН,
F3 = 20 кН, α1 = 70 о,
α1 F2 x α2 = 30 о.
α2 Определить: R.
F3
Рис.1
Решение.
1. Аналитический метод.
Сначала надо определить проекции заданных сил на оси координат, после чего легко найти проекцию равнодействующей силы на эти оси.
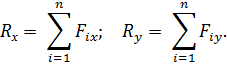
Величину равнодействующей найдем по формуле
Строим схему с соблюдением заданных углов α1 и α2 (без соблюдения масштаба сил, рис 2).
y
x
Рис.2
Для вычисления проекций сил сначала определяем знак проекции, а затем ее абсолютную величину. Проекция положительна, если угол между положительным направлением оси и силой меньше 900 (сила и ось направлены в одну сторону); в противном случае проекция отрицательна. Чтобы получить величину проекции, надо умножить величину силы на косинус угла между силой и ее проекцией (т.е. всегда берется косинус острого угла).
Проекция равнодействующей силы:
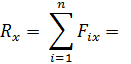
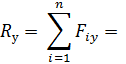
ее величина
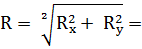
2.Графический метод.
Выберем масштаб сил: m = 10кН/см, тогда силы F1, F2, F3 будут откладываться отрезками:
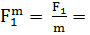
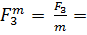
Рис.3
R = см
R = · m = ·10 = кН.
Задача №2.
Определить усилия в стержнях АС и АВ, возникающие от силы F, приложенной к узлу А, аналитическим и графическим методами (рис.4).
ВF Дано: F = 70 кН.
60о 90о
30о А
С
Рис.4
Определить: усилия NАВ и NАС.
Решение:
В F N1 F
60о 1 1
30о 90о 30o
С 2 А N2 A
Рис.5 Рис.6
1. Строим схему, соблюдая все заданные углы (без соблюдения масштаба сил, рис.5). Рассматриваем равновесие точки А, в которой сходятся все стержни и внешние силы.
2. Отбрасываем связи АВ и АС, заменяя их усилиями в стержнях N1 и N2. Направление усилий примем от узла А, предполагая стержни растянутыми. Выполним на отдельном чертеже схему действия сил в точке А (рис.6).
3. Выберем систему координат таким образом, чтобы одна из осей совпала с неизвестным усилием. Составляем уравнения равновесия плоской системы сходящихся сил:
