Формулировка теоремы об изменении кинетической энергии
Перепишем систему дифференциальных уравнений движения механической системы (3.27) через производные по времени от скоростей точек:
 . .
| (3.53) |
Как уже отмечалось в кинематике (параграф 2.1.2), элементарное перемещение связано с элементарным путем соотношением  (где
(где 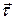 - орт касательной к траектории точки). В некоторых случаях удобно элементарное перемещение выражать через параметры, связанные с естественными осями.
- орт касательной к траектории точки). В некоторых случаях удобно элементарное перемещение выражать через параметры, связанные с естественными осями.
Введем вектор элементарного пути 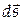 как вектор, численно равный ds и направленный вдоль касательной по скорости:
как вектор, численно равный ds и направленный вдоль касательной по скорости:  . Видно, вектор элементарного пути – это вектор элементарного перемещения, выраженный через естественные оси.
. Видно, вектор элементарного пути – это вектор элементарного перемещения, выраженный через естественные оси.
С учетом сказанного можно из (2.17) получить:
 . .
| (3.54) |
Перемножая левые и правые части равенства (3.54) и k -го уравнения в (3.53) соответственно, получим: 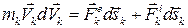 . Используя правила дифференцирования, введем под знак дифференциала в левой части скорость
. Используя правила дифференцирования, введем под знак дифференциала в левой части скорость  и константу
и константу  :
:
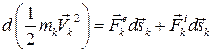 .
.
Скалярный квадрат вектора скорости можно заменить квадратом его модуля:  . Тогда предыдущее выражение примет вид
. Тогда предыдущее выражение примет вид
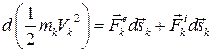 . .
| (3.55) |
Преобразовав таким образом все уравнения системы (3.53), можно сложить почленно все левые и правые части почленно. Получим:
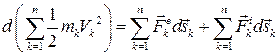 . .
| (3.56) |
(Здесь также использовано свойство равенства суммы дифференциалов и дифференциала суммы).
Введем два определения.
· Кинетическая энергия Т (или энергия движения) есть половина суммы произведений масс точек тела на квадраты скоростей их движений:
 . .
| (3.57) |
Заметим, что исходя из определяющей формулы (3.57), размерность кинетической энергии составляет: кг·м2/с2 = кг·(м/с2) ·м = Н·м =Дж (джоуль).
· Элементарная работа  есть скалярное произведение векторов силы и элементарного перемещения:
есть скалярное произведение векторов силы и элементарного перемещения:
 = =  . .
| (3.58) |
Следует заметить, что аргументом в выражении для элементарной работы является сила 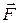 , что отражено в одной из форм записи (3.58).
, что отражено в одной из форм записи (3.58).
Используя введенные понятия, уравнение (3.56) можно записать в виде теоремы об изменении кинетической системы в дифференциальной форме:
 , ,
| (3.59) |
где  - соответственно, элементарные работы k -й внешней и внутренней силы.
- соответственно, элементарные работы k -й внешней и внутренней силы.
Проинтегрировав обе части (3.59) в пределах, соответствующих перемещению (переходу) системы из некого начального положения (состояния) с энергией Т 0в положение (состояние) с энергией Т 1, получим теорему об изменении кинетической системы в интегральной форме:
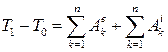 . .
| (3.60) |
Здесь величины  и
и  носят названия работ внешних и внутренних сил на конечном перемещении.
носят названия работ внешних и внутренних сил на конечном перемещении.
Теорема об изменении кинетической энергии, как для точки, так и для механической системы, формулируется одинаково:
Изменение кинетической энергии равно работе всех приложенных сил.
Замечание
В сформулированных выше теоремах о движении центра масс, изменения количества движения и теоремы моментов внутренние силы не фигурируют. В отличие от них, в теореме об изменении кинетической энергии внутренние силы присутствуют в явном виде.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Приведите формулировку теоремы об изменении кинетической энергии.
2. Как определяется кинетическая энергия?
3. Элементарная работа силы – это (…)?
Разберем подробнее понятия кинетической энергии и работы.
Кинетическая энергия
Вернемся к определению кинетической энергии (3.57). Рассмотрим ряд случаев.
1. Система состоит из одной материальной точки, n =1.
В этом случае сумма в выражении (3.57) состоит из одного слагаемого, а формула для кинетической энергии материальной точки приобретет вид:
 . .
| (3.61) |
Кинетическая энергия материальной точки равна половине произведения массы точки на квадрат ее скорости движения.
Отсюда следует, что кинетическая энергия механической системы точек есть совокупная энергия всех ее точек.
2. Механическая система представляет собой абсолютно твердое тело.
a) Тело движется поступательно.
При поступательном движении все точки тела движутся с одинаковыми скоростями, т.е.  . Подставив в формулу (3.57), получим:
. Подставив в формулу (3.57), получим: 
 Сумма масс точек равна массе m системы, откуда выражение для кинетической энергии при поступательном движении в точности соответствует энергии движения материальной точки.
Сумма масс точек равна массе m системы, откуда выражение для кинетической энергии при поступательном движении в точности соответствует энергии движения материальной точки.
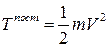 ; ;
| (3.62) |
Кинетическая энергия тела при поступательном движении равна половине произведения массы тела на квадрат скорости центра масс.
b) Твердое тело вращается вокруг неподвижной оси (например, оси Оz)
При вращении скорости точек тела пропорциональны их удаленности от оси и угловой скорости:  . После подстановки в (3.57), имеем:
. После подстановки в (3.57), имеем:  Сумма в полученном выражении – ни что иное, как осевой момент инерции тела JZ, поэтому выражение для кинетической энергии тела при его вращении приобретет вид:
Сумма в полученном выражении – ни что иное, как осевой момент инерции тела JZ, поэтому выражение для кинетической энергии тела при его вращении приобретет вид:
 ; ;
| (3.63) |
Кинетическая энергия вращательного движения тела равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости.
c) Общий случай движения тела [7].
Воспользуемся формулой для оценки скорости точки тела через полюс (2.70), выбрав в качестве полюса центр масс тела:
 . Подставим в (3.57), учитывая, что возможность замены квадрата вектора скорости квадратом его модуля:
. Подставим в (3.57), учитывая, что возможность замены квадрата вектора скорости квадратом его модуля:
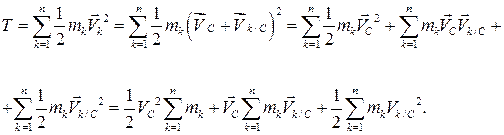
Формально сумма во втором слагаемом представляет собой механический импульс тела в системе отсчета, связанной с его центром масс, и он, в соответствии с (3.33), равен  . Здесь
. Здесь  - скорость центра масс относительно его же самого, т.е. ноль. Сумма в первом слагаемом – масса тела. Подставив выражения для скорости точек тела при его вращении вокруг центра масс в виде:
- скорость центра масс относительно его же самого, т.е. ноль. Сумма в первом слагаемом – масса тела. Подставив выражения для скорости точек тела при его вращении вокруг центра масс в виде:  , получим:
, получим:
 . Последняя сумма – это момент инерции тела относительно его центральной оси (J C), поэтому окончательно имеем:
. Последняя сумма – это момент инерции тела относительно его центральной оси (J C), поэтому окончательно имеем:
 . .
| (3.64) |
Кинетическая энергия твердого тела равна сумме кинетической энергии поступательного движения со скоростью центра масс и кинетической энергии вращательного движения вокруг оси, проходящей через центр масс.
3. Механическая система представляет собой совокупность абсолютно твердых тел.
Здесь вывод сформулировать просто: кинетическая энергия системы равна сумме кинетических энергий этих тел.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Как определяется кинетическая энергия при поступательном движении тела?
2. Как определяется кинетическая энергия тела при его вращении?
3. Найдите формулу для оценки кинетической энергии однородного диска массой m, катящегося без проскальзывания со скоростью своего центра V C.
Работа
Как уже определено формулой (3.58), элементарная работа есть скалярное произведение вектора силы на вектор элементарного перемещения. Рассмотрим подробнее (рис.3.10).

Рис.3.10
Операцию скалярного произведения двух векторов можно, согласно правилам векторной алгебры, представить в разных формах:
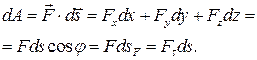 . .
| (3.65) |
Здесь  - вектор элементарного (бесконечно малого) перемещения, его модуль и проекции на оси,
- вектор элементарного (бесконечно малого) перемещения, его модуль и проекции на оси,  - вектор силы, ее модуль и проекции, φ – угол между касательной осью τ и силой,
- вектор силы, ее модуль и проекции, φ – угол между касательной осью τ и силой, 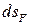 - проекция перемещения на направление силы,
- проекция перемещения на направление силы,  - проекция силы на касательную ось.
- проекция силы на касательную ось.
Исходя из определяющей формулы (3.65), размерность работы составляет Н·м = Дж (джоуль).
Найдем работу силы на конечном перемещении, проинтегрировав последнее выражение в (3.65) в пределах, связанных с начальным и конечным положениями точки приложения силы на траектории ее движения:

| (3.66) |
Геометрически, как определенный интеграл, работа на конечном перемещении соответствует площади криволинейной трапеции под графиком касательной силы от криволинейной координаты s (рис.3.11).

Рис.3.11
Определим, как вычисляется работа у разных сил.
1. Работа силы тяжести.

Рис.3.12
Пусть точка М приложения силы тяжести  перемещается по траектории (рис.3.12), высота точки относительного некого уровня - h, элементарные перемещение и изменение высоты точки -
перемещается по траектории (рис.3.12), высота точки относительного некого уровня - h, элементарные перемещение и изменение высоты точки - 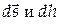 . Используя формулу (3.65), и учтя, что угол φ – тупой, с помощью тригонометрических формул приведения найдем выражение для элементарной работы силы тяжести:
. Используя формулу (3.65), и учтя, что угол φ – тупой, с помощью тригонометрических формул приведения найдем выражение для элементарной работы силы тяжести:
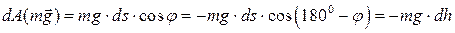 ,
,
или окончательно:
 . .
| (3.67) |
Работа силы тяжести на перемещении точки из положения М0 в положение М1 найдем, интегрируя (3.67):

Введя изменение высоты Δh = h 1 -h 0, получим:
 . .
| (3.68) |
Работа силы тяжести равна принятому с обратным знаком произведению модуля силы на приращение высоты точки ее приложения.
Формулы (3.67) и (3.68) показывают, что:
− при увеличении высоты работа силы тяжести отрицательная;
− при снижении высоты работа силы тяжести положительная.
Легко заметить еще одно свойство выражения (3.68): результат не зависит от траектории перемещения точки М из одного крайнего положения в другое. Отсюда же вытекает и то, что если начальная и конечная точки совмещены (Δh =0), формула приводит к нулевому результату.
Сила, работа которой не зависит от траектории ее перемещения из начального в конечное положение, или сила, работа которой на замкнутой траектории равна нулю, называется потенциальной.
Таким образом, сила тяжести – потенциальная сила.
Включим в скобку (3.68) mg:  . Назовем функцию:
. Назовем функцию:
Π(m  )= mgh, )= mgh,
| (3.69) |
потенциальной энергией силы тяжести (“potency” - сила, возможность, могущество). Тогда выражения (3.67) и (3.68) приобретут вид:
 , ,
| (3.70) |
 . .
| (3.71) |
Отметим, что работа потенциальной силы тяжести не зависит от выбора расположения уровня начального отсчета высоты, поскольку в выражении (3.71) фигурирует не сама потенциальная энергия Π, а ее разница  .
.
2. Работа силы упругости.
Будем считать, растяжение λ пружины жесткостью с направлено по оси О x, причем точка отсчета (т.О) для нее совпадает с положением края недеформированной пружины. Тогда проекция силы упругости (3.14) на ось О x определяется формулой  (сила упругости направлена против направления деформации пружины). Из выражения (3.65) следует:
(сила упругости направлена против направления деформации пружины). Из выражения (3.65) следует:
 ,
,
а работа силы упругости на конечном перемещении:
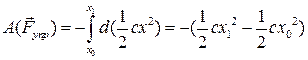 .
.
Если ввести функцию «потенциальная энергия деформированной (сжатой или растянутой) пружины» в виде:
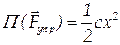 , ,
| (3.72) |
то формулы для оценки работы силы упругости примут вид (3.70) и (3.71).
Таким образом, сила упругости – потенциальная сила.
3. Работа силы трения.
Как уже было показано при анализе сил трения, следует различать силу трения покоя и силу трения скольжения. В первом случае перемещение точки приложения силы отсутствует, а значит и работа силы трения покоя равна нулю. Во втором случае угол между перемещением 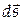 и силой трения скольжения
и силой трения скольжения 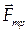 равен 180о, а значит, работа силы трения определяется формулами (используя 3.65 и 3.66):
равен 180о, а значит, работа силы трения определяется формулами (используя 3.65 и 3.66):
 . .
| (3.73) |
где путь  , f – коэффициент трения, N – нормальная реакция опоры. В случае постоянной величины силы трения работа силы приобретает вид, показанный в нижней строчке (3.73).
, f – коэффициент трения, N – нормальная реакция опоры. В случае постоянной величины силы трения работа силы приобретает вид, показанный в нижней строчке (3.73).
Работа силы трения равна произведению силы трения и пути со знаком минус.
Следует заметить, что работа силы трения всегда отрицательна, поскольку при изменении направления перемещения на обратное, автоматически разворачивается в противоположную сторону и вектор силы трения.
Сила, работа которой на любом перемещении отрицательная, называется диссипативной.
Таким образом, сила трения, а также все силы, направленные постоянно против скорости (сила вязкого трения, сила аэрогидродинамического сопротивления и т.д.) являются диссипативными силами.
4. Работа пары сил (работа момента).
Пусть к вращающемуся телу приложен момент М в плоскости его вращения (для простоты рассмотрим только плоское движение). Воспользуемся свойствами пар. Заменим момент парой сил с модулями  где h –плечо пары, и приложим эти силы так, чтобы одна из сил пары была приложена к неподвижной оси вращения тела. Тогда работу будет выполнять только вторая сила пары на элементарном перемещении
где h –плечо пары, и приложим эти силы так, чтобы одна из сил пары была приложена к неподвижной оси вращения тела. Тогда работу будет выполнять только вторая сила пары на элементарном перемещении 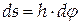 , где
, где  -элементарный угол поворота тела. Учитывая, что перемещение точки при вращении тела и сила пары направлены перпендикулярно плечу и радиусу h, работа силы пары будет:
-элементарный угол поворота тела. Учитывая, что перемещение точки при вращении тела и сила пары направлены перпендикулярно плечу и радиусу h, работа силы пары будет:
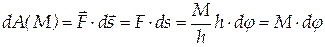 . .
| (3.74) |
Элементарная работа пары сил равна произведению момента пары на элементарный угол поворота тела.
Применим формулу (3.74) для оценки работы момента трения качения (3.13), учтя противоположность направление момента и качения тела:
 . .
| (3.75) |
Вывод формул для работы момента на конечном угле поворота предоставим читателю.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Как определяется величина работы силы тяжести и ее знак?
2. Нужна ли и откуда берется энергия для поддержания движения планет на круговых орбитах вокруг Солнца?
3. Может ли работа силы трения быть положительной? Если нет, то за счет чего возрастает скорость и кинетическая энергия автомобиля при его разгоне? Ответ сформулируйте на основе использования теоремы об изменении кинетической энергии.
Закон сохранения механической энергии
Полученные при рассмотрении работ силы тяжести и силы упругости соотношения (3.70) и (3.71) являются универсальными для всех видов потенциальных сил. Кроме сил тяжести и упругости, к потенциальным силам относятся: силы гравитационного притяжения, силы электростатического взаимодействия, силы поверхностного натяжения и ряд других.
Рассмотрим случай, когда все действующие в системе силы являются потенциальными. Заменим в теореме об изменении кинетической энергии (3.59) работу каждой силы на убывание потенциальной энергии (3.70):
 .
.
Введя понятие «потенциальная энергия системы» П, как алгебраическая сумма потенциальных энергий сил системы, получим:  . Окончательно:
. Окончательно:
 . .
| (3.76) |
Это - закон сохранения механической энергии в системе с потенциальными силами, если ее так определить: механическая энергия есть сумма кинетической и потенциальной энергий всей системы. Из выражения (3.76) видно, что механическая энергия в потенциальной системе сохраняет свою величину (“conservation” – сохранение). Отсюда второе название потенциальных сил и систем – консервативные силы и системы, т.е. те, которые сохраняют механическую энергию.
Сформулируем закон сохранения механической энергии:
Механическая энергия в консервативных системах, где действуют только потенциальные силы, не меняется со временем.
Мощность
Определим такую энергетическую характеристику как мощность следующим образом: мощность – производная по времени от работы, или скорость выполнения работы, или, что одно и то же, работа, выполняемая силой за единицу времени:
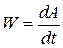 . .
| (3.77) |
Размерность мощности – Дж/с = Вт (ватт). Если подставить в (3.77) разные представления элементарной работы из (3.65), получим:
 . .
| (3.78) |
Из формул (3.78) легко видеть, что мощность зависит от угла φ между силой и скоростью. При φ = 0мощность максимальна и равна 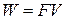 , при φ = 90о мощность равна нулю.
, при φ = 90о мощность равна нулю.
Используя выражение для работы момента (3.74), можно оценить мощность пары сил, приложенных к вращающемуся телу:
 . .
| (3.79) |
Мощность равна скалярному произведению силы на скорость точки приложения силы, а также произведению (вращающего) момента на угловую скорость вращения.
Из приведенных формул для оценке мощности следует, что если от источника с заданной мощностью нужно получить большую силу или момент, то это возможно сделать только при снижении скорости или угловой скорости. Так, например, когда железнодорожному локомотиву надо увеличить тягу, то для этого необходимо уменьшить скорость поезда.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Рассмотрите, как меняется кинетическая и потенциальная энергии при колебании маятника.
2. Попробуйте сформулировать определение понятия «средняя мощность».
3. Для чего нужна автомобилю коробка передач? Объясните, использую приведенный выше пример с локомотивом.
[1] Первичное определение динамики - см. «Введение».
[2] Первичное определение понятия «сила» - см. «Введение».
[3] Определение внешних и внутренних сил – параграф 1.1.1 раздел «Статика».
[4] Следует отметить, что так или приблизительно так формулируются задачи динамики, как для точки, так и для тела или механической системы
[5] Ссылка на внешние силы не имеет смысла при рассмотрении движения одной материальной точки (у точки нет внутренних сил), поэтому для сохранения общности формулировки, как для точки, так и для системы, слово «внешние» поставлено в скобках.
[6] Ось тела называется центральной, если она проходит через центр его масс.
[7] Плоскопараллельное движение можно здесь рассматривать, как частный случай общего движения.






