Для студентів заочної форми навчання зі спеціальності „Інформатика”.
1 Вирішити методом послідовних наближень інтегральне рівняння Фредгольма другого роду (з точністю 10%):
1.1 
.
1.2 
.
1.3 
.
1.4 
.
1.5 
.
1.6 
.
1.7 
.
1.8 
.
1.9 
.
1.10 
.
1.11. 
1.12 
.
1.13 
.
1.14 
.
1.15 
.
1.16 
.
1.17 
.
1.18 
.
1.19 
.
1.20 
.
1.21 
.
1.22 
.
1.23 
.
1.24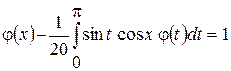 
.
1.25 
.
1.26 
.
1.27 
.
1.28 
.
1.29 
.
1.30 
.
1.31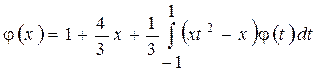 
.
1.32 
.
1.33 
.
2 Вирішити методом послідовних наближень інтегральне рівняння Вольтерра другого роду з точністю 10% (там, де не вказано окремо, інтервал ізоляції кореня 
):
2.1 
.
2.2 
.
2.3 
.
2.4 
.
2.5 
.
2.6 
.
2.7 
.
2.8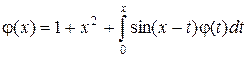 
.
2.9 
.
2.10 
.
2.11 
.
2.12 
.
2.13 
.
2.14 
.
2.15 
.
2.16 
.
2.17 
.
2.18 
.
2.19 
.
2.20 
.
2.21 
.
2.22 
.
2.23 
.
2.24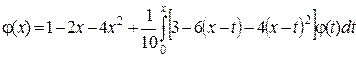 
.
2.25 
.
2.26 
.
2.27 
.
2.28 
.
2.29 
.
2.30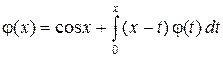 
.
2.31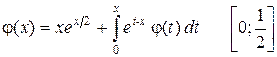 
.
2.32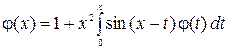 
.
2.33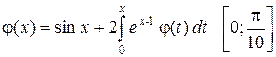 
.
Приклад 1
Розв’язати з точністю до 10% інтегральне рівняння Фредгольма 2-го роду методом послідовних наближень:
.
Перевіримо, чи є інтегральний оператор стискуючим, тобто, чи виконується умова:
,
де 
; 
; 
.
Знаходимо 
.
,
.
Таким чином,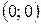 
є критичною точкою і 
.
На границі області
.
,
.
,
,
– при 
немає критичних точок.
.
Таким чином,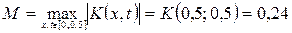 
. Маємо: 
.
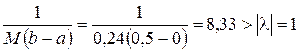Ми можемо застосувати метод послідовних наближень.
Нехай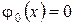 
, звідки
.
.
Для обчислювання необхідної кількості ітерацій, які потрібно зробити щоб досягти завдану точність обчислень, скористаємося формулою:
де 
гіпотетичний точний розв’язок,
наближення,
Маємо:
При 
маємо: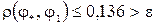 
Тобто 
буде наближеним розв’язком вихідного інтегрального рівняння Фредгольма з точністю 0,1.
Знайдемо 
:
Відповідь: 
Приклад 2
Розв’язати інтегральне рівняння Вольтерра 2-го роду методом послідовних наближень:
на з точністю 10%.
Оператор Вольтерра є стискуючим завжди, тому ми можемо застосувати метод послідовних наближень.
Нехай 
, тоді
;
;
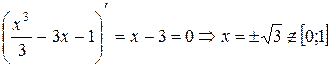– критичних точок немає.
На кінцях відрізку 
:
,
.
Таким чином,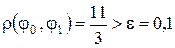 
.
Для оцінки кількості наближень, необхідних для виконання заданої точності обчислень скористаємося формулою:
Маємо 
при 
Тобто 
буде розв’язком вихідного інтегрального рівняння Вольтерра з точністю 10%.
Знайдемо послідовно 
та :
,
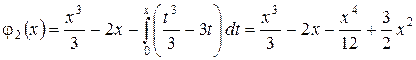Відповідь: 
Правила виконання та оформлення
Контрольних робіт
При виконанні контрольних робіт необхідно суворо дотримуватися нижчезазначених правил. Роботи, які виконані без урахування цих правил, не зараховуються і повертаються студенту на доопрацювання.
1 Кожна контрольна робота повинна виконуватися в окремому зошиті в клітинку чорнилами темного кольору (крім червоного). Необхідно залишати поля шириною 3-4 см для зауважень рецензента.
2 На обкладинці зошита необхідно чітко зазначити: назву дисципліни, назву навчального закладу, факультет, групу, прізвище, ім'я та по батькові, номер залікової книжки і номер варіанта. У кінці роботи слід поставити дату її виконання та особистий підпис.
3 Робота має містити всі задачі, які зазначені у завданні строго за своїм варіантом. Контрольні роботи, які містять не всі задачі або задачі не свого варіанта, не зараховуються.
4 Перед розв'язуванням кожної задачі необхідно повністю записати її умову.
5 Розв'язання задач слід викладати докладно, акуратно, пояснюючи і обґрунтовуючи усі дії за ходом розв'язання.
6 Після отримання прорецензованої роботи, як зарахованої, так і незарахованої, студент повинен виправити усі відмічені рецензентом помилки та недоліки і записати їх після рецензії під заголовком "Виправлення" у цьому ж зошиті.
За необхідності можна виправлення записати в іншому зошиті та підклеїти його до основного.
