СУМСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ
Методичні вказівки
для організації самостійної роботи
по курсу "Функціональний аналіз"
для студентів заочного відділення
спеціальності „ Інформатика”
ЗАТВЕРДЖЕНО
На засіданні кафедри
прикладної математики і механіки
Протокол № 1 від 30.08.04
Суми – 2004
Вступ
Курс функціонального аналізу, що викладається студентам спеціальності „Інформатика”, згідно робочої програми, розробленої на основі „Освітньо-професійної програми вищої освіти”, індекс 7.0802.02, переслідує наступні цілі:
Навчити студентів найбільш загальним математичним методам розв’язування задач обчислювальної, прикладної математики, фізики та інших природничих наук.
Дати студентам єдиний погляд на різноманітні розділи математики, такі як математичний аналіз, інтегральні та диференціальні рівняння, варіаційне числення, криптографія і т.п.
В результаті вивчення дисципліни студент повинен:
ЗНАТИ:
· елементи теорії метричних просторів, простори 
· елементи теорії лінійних нормованих просторів;
· основні означення теорії Евклідових та Гільбертових просторів;
· елементи теорії лінійних функціоналів та операторів.
УМІТИ:
· знаходити відстані між елементами в різних просторах;
· застосувати принцип нерухомої точки до розв’язування рівнянь (скалярних, систем лінійних рівнянь, інтегральних рівнянь і т.п.);
· будувати ортонормовані системи за допомогою процесу ортогоналізації Шмідта.
Курс „Функціональний аналіз” викладається студентам спеціальності „Інформатика” у 6-му семестрі.
Забезпечуючи навчальні дисципліни: математичний аналіз, алгебра і геометрія, теорія функцій дійсної змінної.
Матеріал дисципліни використовується в курсах теорії інформації, теорії алгоритмів.
Основними розділами (питаннями) даної дисципліни є:
1. Метричні простори.
2. Лінійні нормовані простори.
3. Гільбертові простори.
4. Лінійні функціонали в ЛНП.
Структура курсу складається з наступних блоків:
· Метричні простори.
· Лінійні нормовані простори.
· Евклідові простори.
· Гільбертові простори.
Лекційний матеріал викладається на настановчій сесії відповідно до таблиці 1.
1 Лекції
| Номер розділу | Ном. підрозділу чи теми | Назви розділів, підрозділів, тем, та основні питання, що розглядаються | Обсяг, год. | Посилання на літературу |
Метричні простори. Означення метричного простору. Приклади метричних просторів, простори  Метрика. Ізометрія метричних просторів. Метрика. Ізометрія метричних просторів.
| 1,5 | 3.1.1: [1]-[3]. 3.1.3: [1] | ||
| Повні метричні простори. Критерій Коші. Приклади. Лема про замкнені кулі. Принцип стискуючих відображень (ПСВ). Теорема Банаха. Застосування ПСВ для розв’язку скалярних рівнянь, СЛАР. | 3.1.1: [1]-[3]. 3.1.3: [1] |
| Лінійні нормовані простори (ЛНП). Лінійні простори. Базис, підпростір, норма, зв’язок з метричним простором. Приклади ЛНП. Ізоморфізм. Банахові простори. Приклади. | 1,5 | 3.1.1: [1]-[4]. 3.2.1: [1] | ||
| Евклідові та Гільбертові простори. Скалярний добуток, норма. Приклади Евклідових та Гільбертових просторів. Характеристична властивість Гільбертових просторів. Ортонормовані системи в Н. Процес ортогоналізації Шмідта. | 1,5 | 3.1.1: [1]-[4]. 3.1.3: [1] | ||
| Апроксимація в Н. Відстань від елемента до підпростору. Теорема про проекцію в Н.Ортогональна декомпозиція. | 1,5 | 3.1.1: [1]-[3] | ||
| Всього за семестр |
Практичні заняття відповідно до таблиці 2.
2 Практичні заняття
| Номер заняття | Номер розділу | Найменування та зміст практичної роботи | Обсяг, год. | Посилання на літературу | Примітки |
| Метричні простори. | 3.1.1: [3], 3.3.1: [1] |
| Принцип стискуючих відображень. Різноманітні застосування. | 3.1.1: [2], [3] | ||||
| Побудова ортонормованих систем в Евклідовому просторі. | 3.1.1: [1], 3.3.1: [1] | ||||
| Всього за семестр |
На настановчій сесії видається завдання на контрольну роботу, яку студент повинен виконати в період між сесіями. Текст контрольної роботи і варіанти контрольних завдань приводяться нижче.
У заліково-екзаменаційній сесії студентам видається перелік контрольних теоретичних питань, по яким вони повинні підготуватися до заліку з курсу „Функціональний аналіз”.
Передбачаються також консультації студентів у період між сесіями, а також безпосередньо перед проведенням заліку.
Текст контрольних питань
1. Метричні простори. Аксіоми метрики. Простори  .
.
2. Метричні простори. Аксіоми метрики. Простори послідовностей  .
.
3. Метричні функціональні простори.  .
.
4. Метричні функціональні простори 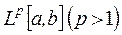 .
.
5. Повнота. Приклади метричних просторів.
6. Теорема про замкнені кулі.
7. Принцип стискуючих відображень (ПСВ).
8. Застосування ПСВ до розв’язування скалярних рівнянь.
9. Застосування ПСВ до розв’язування СЛАР.
10. Лінійний многовид. Лінійна залежність векторів. Базис.
11. Лінійні нормовані простори. Аксіоми норми. Відповідність метричним просторам.
12. Банаховий простір  .
.
13. Банаховий простір  .
.
14. Банаховий простір  .
.
15. Підпростір в ЛНП, приклади підпросторів.
16. Евклідові простори. Скалярний добуток, норма. Приклади Евклідових просторів.
17. Характеристична властивість Евклідових просторів.
18. Лінійний многовид. Підпростір. Базис в ЛНП.
19. Ортонормовані системи в Евклідових просторах. Процес ортогоналізації Шмідта.
20. Теорема рахованості ортонормованої системи в сепарабельному Евклідовому просторі.
21. Ортонормований базис в Евклідовому просторі. Навести приклад.
22. Евклідовий простір  .Скалярний добуток, норма, ортонормованих базис.
.Скалярний добуток, норма, ортонормованих базис.
23. Евклідовий простір  . Скалярний добуток, норма, ортонормованих базис.
. Скалярний добуток, норма, ортонормованих базис.
24. Евклідовий простір  . Скалярний добуток, норма, ортонормованих базис.
. Скалярний добуток, норма, ортонормованих базис.
25. Гільбертові простори. Приклади ГП.
26. Апроксимація в ГП. Відстань від елемента  до підпростору.
до підпростору.
27. Теорема о проекції в Н.
28. Ортогональна декомпозиція в Н.
При самостійній роботі студентів по розділу 1, рекомендується використовувати посібник 3.1.3 – [1] (стор. 6 – 24).
У розділу 2 особливу увагу необхідно приділити принципу стиснених відображень (3.1.3 – [1], стор. 34 -41). Цей принцип буде використаний при виконанні контрольної роботи.
Суттєво використовується в прикладній математиці й інформатиці Гільбертів простір Н, ортогональні системи елементів з Н, ряди Фур'є в Н, проблема апроксимації в Н. У зв'язку з цим особливу увагу необхідно приділити вивченню (або хоча б ознайомленню) геометрії Гільбертова простору, знати приклади конкретних Гільбертових просторів l2, L2. Цей матеріал, сконцентрований у розділах 4 - 5, можна вивчати по багатьом джерелам (3.1.1 – [1], 3.1.2 – [1], 3.1.3 – [1], стор.99 – 133).
Перед виконанням контрольної роботи необхідно переглянути в конспекті лекцію з розділу 2, потім уважно прочитати стор. 34 -40 у посібнику 3.1.3 – [1].
Треба мати на увазі, що «Функціональний аналіз» складна математична дисципліна, що має справу з абстрактними поняттями, об'єктами й операціями. Тому наявні в літературі керівництва досить складні для первісного засвоєння, особливо коли в читача дефіцит часу. У цьому змісті, навчальний посібник 3.13 – [1] є більш легким для сприйняття, тому що він адаптован до студентської аудиторії Сумського державного університету.
Рекомендована література
| № п/п | Найменування навчально-методичної літератури | Кіль-кість екз. | Вид |
| 3.1.1 | Основна література | ||
| Люстерник Л.А., Соболев В.И. Элементы функционального анализа. М.: Наука, 1965 | Моногр. | ||
| Колмогоров А., Фомин С. Элементы теории фунций и функционального анализа.-М.: Наука, 1976 | Підр. | ||
| Шилов Г.Е. Математический анализ. Специальный курс.-М.: Физматгиз, 1960 | Підр. | ||
| 3.1.2 | Додаткова література | ||
| Смирнов В.И. Курс высшей математики, т.5.-М.-Л., 1960 | Моногр. | ||
| 3.1.3 | Науково-методична література видавництва СумДУ | ||
| Фильштинский Л.А. Элементы функциионального анализа с приложениями. Часть 1. – Сумы: СумГУ, 1998 | Навч. посібник | ||






