Пример выполнения задания – рисунок 3 страница 11.
Исходные данные – таблица 1.
| Индивидуальные задания к эпюру №1 | |||||||||||||||
| Номер варианта | A | B | C | D | E | ||||||||||
| X | Y | Z | X | Y | Z | X | Y | Z | X | Y | Z | X | Y | Z | |
| Продолжение таблицы 1 | |||||||||||||||
| Номер варианта | A | B | C | D | E | ||||||||||
| X | Y | Z | X | Y | Z | X | Y | Z | X | Y | Z | X | Y | Z | |
| Продолжение таблицы 1 | |||||||||||||||
| Номер варианта | A | B | C | D | E | ||||||||||
| X | Y | Z | X | Y | Z | X | Y | Z | X | Y | Z | X | Y | Z | |

Рис. 3. Пример выполнения эпюра № 1
ЭПЮР №2
Содержание задания
По заданным двум проекциям целого геометрического тела построить третью проекцию и:
1. Найти три проекции наложенного сечения.
2. Определить истинную величину фигуры сечения.
3. Построить развертку усеченной поверхности геометрического тела, сделать выкройку и склеить бумажную модель усеченного тела.
4. Выполнить аксонометрическую проекцию усеченного тела.
Методические указания
Для построения проекций фигуры сечения геометрического тела плоскостью необходимо найти точки пересечения ребер или образующих геометрического тела с секущей плоскостью и полученные точки соединить:
- ломаной линией, если геометрическое тело – многогранник;
- плавной кривой линией, если геометрическое тело образовано замкнутой кривой поверхностью.
В тех случаях, когда секущая плоскость не параллельна ни одной из плоскостей проекций, фигура сечения проецируется с искажением. Поэтому для определения истинной величины фигуры сечения следует применить один из способов преобразования чертежа, например, способ замены плоскостей проекций или способ плоскопараллельного перемещения (как на рисунке 4).
Для построения развертки усеченной части геометрического тела не-обходимо знать истинные размеры ее составляющих. На рисунке 4 основа-ние имеет истинную форму, т.к. оно параллельно плоскости проекций Н.
Для пирамиды длины ребер искажены в том случае, если являются пря-мыми общего положения, поэтому необходимо определить их истинные размеры, например, способом вращения вокруг оси, перпендикулярной одной из плоскостей проекций. Развертку боковой поверхности многогранника можно выполнить последовательным построением граней, учитывая истинные размеры ребер и сторон основания. Боковая поверхность конуса разворачивается в круговой сектор: угол сектора φ = (R / L) ∙ 360°,
Где R - радиус окружности основания конуса
L – длина крайней образующей конуса
Эпюр №2 выполняется на формате А3 (297 х 420 мм).
Отдельно представить бумажную модель усеченного геометрического тела (большую часть).
Пример выполнения задания – рисунок 4 страница 27.
Исходные данные – таблица 2.
Индивидуальные задания к эпюру №2
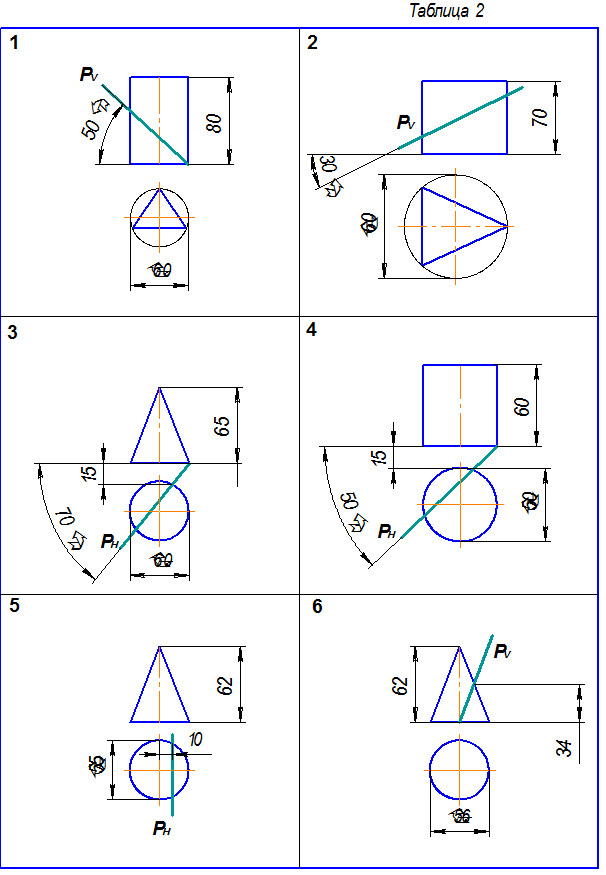













Рис. 4. Пример выполнения эпюра № 2
ЭПЮР №3
Содержание задания
Построить в двух проекциях линию пересечения поверхностей двух геометрических тел.
Задание содержит две части.
Методические указания
Данное задание следует выполнить двумя способами: секущих плоскостей и сфер. Для нахождения точек линии пересечения двух поверхностей необходимо выбрать наиболее рациональный способ решения. При решении эпюра методом вспомогательных секущих плоскостей следует подбирать такие вспомогательные плоскости, которые в пересечении с данными поверхностями могут дать простые для построения сечения, например, треугольники или окружности.
Каким бы способом ни выполнялось построение линии пересечения поверхностей, желательно вначале найти характерные (или «опорные») точки искомой линии. К таким точкам относятся:
- точки, проекции которых лежат на проекциях контурных линий одной из поверхностей, например, на крайних (очерковых) образующих конуса или на главном меридиане (или экваторе) шара, а также точки, отделяющие видимую часть линии пересечения от невидимой;
- «крайние точки» - правые и левые, наивысшие и наинизшие, ближайшие и наиболее удаленные от плоскостей проекций.
Все остальные точки линии пересечения называются промежуточными или случайными.
На чертеже необходимо показать построение опорных точек линии пересечения поверхностей, а также нескольких промежуточных точек.
В выполненном на странице 47 примере вспомогательные секущие плоскости – горизонтальные плоскости уровня (P, R, T, Q). в пересечении данных плоскостей с конусом получаются окружности, которые следует показать на горизонтальной плоскости. В пересечении данных окружностей с горизонтальной проекцией цилиндра получаются точки искомой линии.
Затем в проекционной связи находим фронтальные проекции этих точек.
Способ сфер применяют только в том случае, когда обе поверхности кривые, и их оси пересекаются. При использовании вспомогательных секущих сфер следует сначала найти центр сфер. Центр сфер - это точка пересечения осей вращения пересекающихся тел (точка О´ на рисунке 5). Сначала находят фронтальные проекции точек линии пересечения, а затем горизонтальные (опускаем полученные точки на окружности, в которых они находятся). Минимальная по размерам сфера (обозначена римской цифрой I) проводится касательно к большему геометрическому телу. Затем проводим еще несколько вспомогательных сфер (II, III и т.д.) радиусами побольше. Чем больше вспомогательных сфер проведено, тем точнее будет линия взаимного пересечения поверхностей.
Задание выполнять на формате А3.
Пример выполнения задания – рисунок 5 страница 47.
Исходные данные – таблица 3.

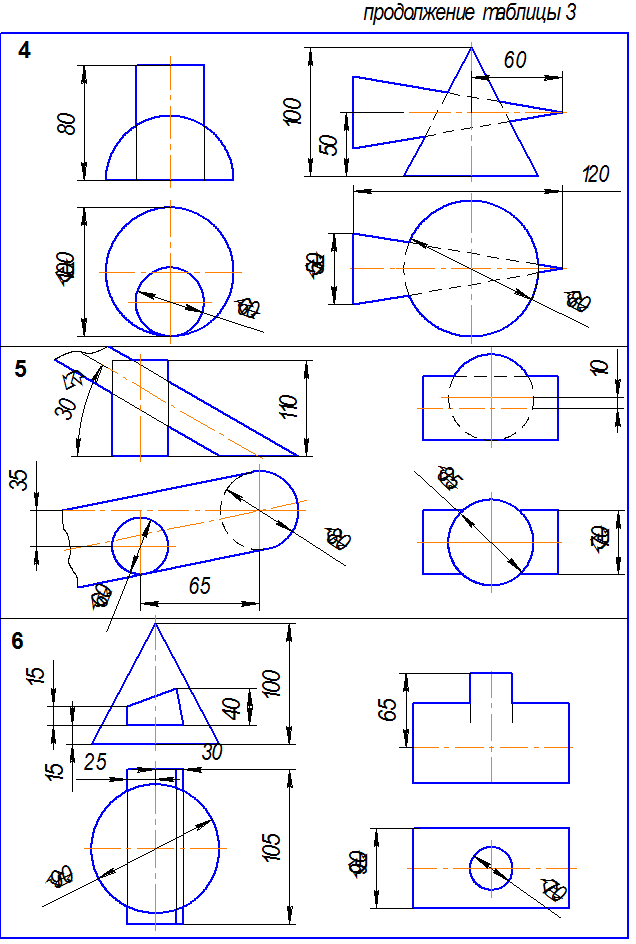









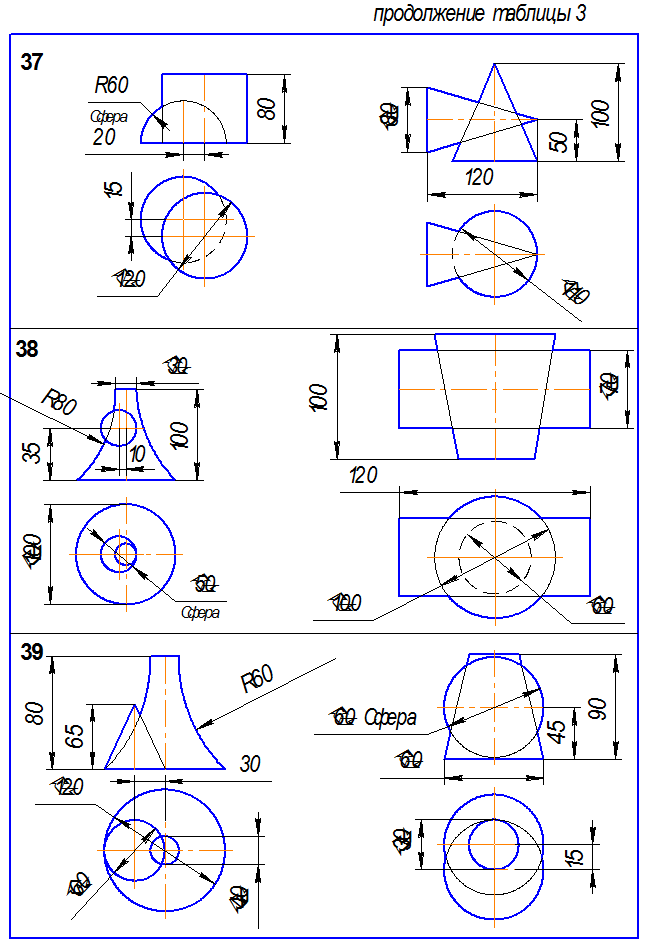
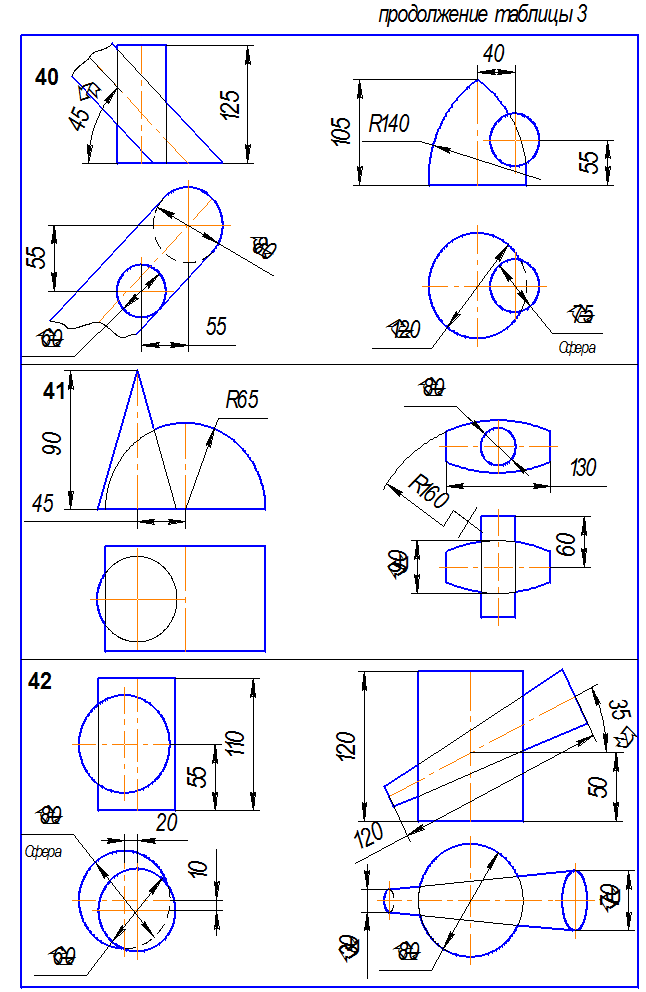





Рис.5. Пример выполнения эпюра № 3
Литература
1. Гордон, В.О. Курс начертательной геометрии / В.О.Гордон,
М.А.Семенцов – Огиевский. – М.: Высшая школа, 2002. – 272 с.
2. Короев, Ю.И. Начертательная геометрия / Ю.И.Короев. – М.:
Стройиздат, 1987. – 319 с.
3. Бубенников, А.В. Начертательная геометрия. – М.: Высшая школа,
1985. – 336 с.
4. Гордон, В.О. Сборник задач по курсу начертательной геометрии /
В.О. Гордон, Ю.Б. Иванов, Т.Е. Солнцева. – М.: Наука, 1989. – 288 с.
Содержание
Введение ……………………………………………………………… 3
1 Требования к оформлению эпюра ………………………………… 3
2 Эпюр № 1 …………………………………………………………….. 5
3 Эпюр № 2 …………………………………………………………….12
4 Эпюр № 3 ……………………………………………………………..15




