Аналитический метод определения параметров маховика

(метод Мерцалова).

Для аналитического решения удобен метод Н. И. Мерцалова.

Вычисляются функции Т₁ и Т₂ соответственно:

(67)

(68)

Величины w_max и w_min определяются по формулам:

ω_mах = ω₁∙(1 + δ/2) = 10,46∙(1+0.05/2) = 10,72 рад^-1; (69)

ω_min = ω₁∙(1 - δ/2) = 10,46∙ (1 - 0,05/2) =10,19 рад^-1. (70)

Записываются получившиеся данные в таблицу 15

 

 

Таблица 12.

	0°	30°	60°	90°	120°	150°	180°	210°	240°	270°	300°	330°
DТ		16,83	2,4	27,2	66,1	103,48	131,8		149,2	135,9	102,5	49,9
Jпр	0.02	0.306	0.620	0.6	0.4	0.185	0.049	0.251	0.213	0.758	1.325	0.566
Т1	-1,15	-0,75	-33,22	-7,27	43,11	92,85	128,18	132,5	136,9	92,34	26,36	17,37
Т2	-1,04	0,94	-29,78	-3,95	45,33	93,87	129,25	133,9	137,9	96,55	33,7	20,5

Для определения момента инерции маховика применяется формула:

J_M = (Т_{1 max} – Т_{2 min} – 1/2(J_{пр max}∙w_max² – J_{пр min}∙w_min²)) / dw₁² (71)

J_{пр max} – значение приведенного момента инерции при j₁, в которых значение T₁(j₁) максимально.

J_{пр min} – значение приведенного момента инерции при j₁, в которых значение Т₂(j₁) минимально.

J_{пр max} (j₁ = 300°) = 1,325 кг м²

J_{пр min} (j₁ = 0°) = 0,02 кг м²

T_{1 max} (j₁ = 240°) = 136,9 Дж

Т_{2 min} (j₁ = 60°) = - 29,78 Дж

J_M = (136,9 – (-29,78) – 1/2(1,325 ∙ 10,72 ² – 0,02∙ 10,19²)) / 0,05 10,46² =

= 30,5 кг м²

Силовой анализ механизма

Силовой анализ проведем для такого положения механизма, при котором угол j₁ будет равен 300⁰.

4.1 Определение линейных и угловых скоростей звеньев.

 

 

Скорость точки А₁ равна скорости точки А₂ и находится по формуле:

 

(72)

 

где: w₁ – угловая скорость звена 1;

– длина звена 1.

Подставляя данные, получаем:

Скорость точки В, принадлежащей звену 2, определяется из следующего уравнения:

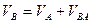(73)

Скорость известна и по величине и по направлению, а скорость известна только по направлению и направлена перпендикулярно линии АВ.

 

Скорость точки С, определяется из следующих уравнений:

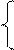
(74)

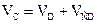(75)

Скорость направлена перпендикулярно линии BС.

Скорость направлена перпендикулярно линии CD.

Скорость точки E, определяется из следующего уравнения:

(76)

Скорость направлена перпендикулярно линии EC.

Зная направления действий скоростей точек, строим план скоростей.

 

 

Таблица 13. - Линейные скорости

	VВ	VCB	VCD	VEC	VE
3000	1.256	0.17	1.2	0.63	0.88

 

Найдем угловые скорости

 

(77)

Таблица 14. – Угловые скорости

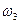
	12.56	0.37	3.6	0.57

 

Определим линейные скорости центров тяжести шатуна 2 и 4.

Используя свойство подобия можно определить скорость любой точки механизма.

Из свойства подобия:

 

(78)

 

(79)

(80)

 

Таблица 15.- Линейные скорости центров тяжести шатуна 2 и 4.

 

VS2	1.25
VS4

Определение линейных и угловых ускорений звеньев.

 

м/с² (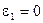) (81)

 

Ускорения точки B будет складываться только из нормальной составляющей, так как вращение происходит с постоянной угловой скоростью, и тангенциальные составляющие ускорений равны нулю.

Ускорение т. B известно по значению и направлено к точке A.

Ускорение точки С можно найти из следующих уравнений.

(82)

(83)

 

(84)

(85)

 

 

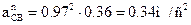
Ускорение точки E можно найти из следующих уравнений.

 

(86)

(87)

(88)

Для решения системы векторных ускорений строим план ускорений.

Построив планы ускорений получим:

Таблица 16.- Линейные ускорения

 

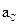
				18.6	8.7

 

Найдем угловые ускорения

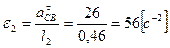(89)

Таблица 17.- Угловые ускорения