Рассмотрим сумму вида S= a1 + a2 + a3 +... пусть имеется положительное число ε > 0, называемое точностью вычислений. Во многих задачах точность вычисления суммы S считается достигнутой, когда выполняется одно из следующих условий:
· разность │Si – Si-1│ < ε, где Si – сумма на i–м шаге цикла (т.е. сумма содержит i слагаемых), а Si-1 – сумма на предыдущем шаге;
· разность │ai – ai-1│< ε, где ai – значение слагаемого на i-м шаге, а
ai-1 – на предыдущем шаге цикла;
· значения │Si│ < ε и значение │ai│ < ε.
Абсолютное значение (модуль) условия обычно требуется для знакопеременных рядов. Следует заметить также, что приведенные выше условия во многих задачах практически эквивалентны.
Кроме вычислений, связанных с рядами, существует много задач, в которых количество повторений цикла определяется в процессе его выполнения. Как уже известно, подобные циклы называют итеративными.
При описании базовых алгоритмов регулярных циклических структур мы приводили примеры вычисления сумм и произведений конечного (заранее известного) числа членов последовательности (Примеры 4.5.2-3, 4.5.2-4, 4.5.2-5).
Рассмотрим теперь некоторую последовательность, содержащую бесконечное число членов: a0, a1, a2, a3,…, ai,…, an,… В таких задачах требуется вычислять члены последовательности до тех пор, пока очередной вычисленный член не будет удовлетворять некоторому условию.
Если задано некоторое число ε, условия окончания итерационного процесса могут, например, быть следующими:
· для убывающей последовательности an < ε;
· для возрастающей последовательности an > ε ( примеры 4.6.2-1, 4.6.2-3,
4.6.2-5 );
· для убывающей знакопеременной последовательности |an| < ε
( пример 4.6.2-4);
· для некоторых других последовательностей | an+1 -an|<ε (пример 4.6.2-2).
Пример 4.6.2-1. Написать процедуру-Function, которая среди последовательности чисел (факториал n! =1*2*3*4*... n) находит первое число, большее заданного значения переменной a.
Алгоритм решения данной задачи относится к алгоритмам вычисления членов бесконечных последовательностей (рис.4.6.2-1).
Этот алгоритм использует итеративный цикл с предусловием и реализуется с помощью конструкции Do While... Loop.
Для решения данной задачи проведем формализацию. Для этого введем следующие обозначения: b – очередной член бесконечной последовательности; n – номер этого члена, который в данной задаче совпадает со значением знаменателя дроби, добавляемой к предыдущему члену для получения значения очередного члена последовательности. Таким образом, итерационная формула вычисления очередного члена последовательности будет иметь следующий вид: (т.е. должны выполняться условия n>=1 AND n<=15), где n – номер члена.
| Function Pr621(ByVal a As Double)As Double Dim b As Double Dim n As Integer b = 1 n = 1 Do While b <= a n = n + 1 b = b + 1 / n Loop Return b End Function |
Рис. 4.6.2-1.Схема алгоритма и программный код процедуры Pr621(),
которая среди последовательности чисел находит первое число,
большее заданного значения, используя оператор Do While...Loop
Примера 4.6.2-1
Процедура-функция Pr621() может быть вызвана из любой другой процедуры или из модуля формы, например, как показано на рис. 4.6.2-2.
| Dim aa, bb As Double aa = vvodDbl2("Введите значение a=", TextBox1) bb = Pr621(aa) vivodDbl1(bb,TextBox2) |
Рис. 4.6.2-2. Пример обращения к процедуре Pr621()
Решение данного примера может быть реализовано также с использованием конструкции Do Until…Loop (рис. 4.6.2-3), а цикл с предусловием можно заменить на цикл с постусловием и соответствующим ему изменением настройки цикла (рис. 4.6.2-4).
| Function Pr623(ByVal a As Double) As Double Dim b As Double Dim n As Integer b = 1 n = 1 Do Until b > a n = n + 1 b = b + 1 / n Loop Return b End Function |
Рис. 4.6.2-3. Схема алгоритма и программный код процедуры Pr621(),
которая среди последовательности чисел находит первое число,
большее заданного значения, и, используя оператор Do Until…Loop
Примера 4.6.2-1
Изменим в цикле условие продолжения выполнения цикла
(на рис. 4.6.2-1 заменим условие b <= a на условие b > a), т.е. будем проводить вычисления членов последовательности до тех пор, пока не встретится член, больший заданного числа. Заменим условие b <= a на условие b > a.
Тогда алгоритм и функция будут выглядеть, как на рис.4.6.2-3.
Если вычисление членов последовательности проводится в теле цикла, начиная с первого, то алгоритм и процедура-функция примут вид, показанный на рис 4.6.2-4.
| Function P624(ByVal a As Double) _ As Double Dim b As Double Dim n As Integer b = 0 n = 0 Do n = n + 1 b = b + 1 / n Loop Until b > a Return b End Function |
Рис. 4.6.2-4. Схема алгоритма и программный код процедуры Pr624(),
которая среди последовательности чисел находит первое число,
большее заданного значения, используя, оператор Do…Loop Until
Примера 4.6.2-1
Мы получили структуру итеративного цикла с постусловием, изменив настройку цикла: n = 0, b = 0. В данном случае условием окончания вычислительного процесса служит значение True логического выражения
b > a, а продолжением – значение False (конструкция Do…Loop Until).
Изменив условие на b <= a, получим конструкцию цикла с
Do…Loop Wile.
Следовательно, задача может быть решена с использованием как цикла с предусловием, так и цикла с постусловием.
Пример 4.6.1-2. Написать процедуру-Function, которая вводит натуральное число n, значение которого находится на отрезке [1;15], с проверкой ввода (т.е. должны выполняться условия n>=1 AND n<=15).
Воспользуемся известной итерационной формулой, где i=0, 1, 2,...; x0=0. Следует закончить итеративный процесс, как только |xi+1-xi| станет меньше ε=10-4.
Для решения этой задачи необходимо из очередного приближения вычисленного корня xi+1 вычитать значение предыдущего приближения корня xi . Для этого при каждом повторении цикла перед вычислением очередного значения корня x сохраняем в переменной a текущее значение x (оно становится предыдущим). Цикл прекращаем, если разность между a (т.е. xi) и x (т.е. xi+1) станет меньше e=10-4.
Алгоритм решения данной задачи относится к итерационным алгоритмам (рис. 4.6.2-5) и может быть реализован, например, с помощью конструкции Do... Loop Until c постусловием.
| Function P625() As Double Dim a, x, d As Double x = 0 d = 1E-4 Do a = x x = -Exp(a) Loop Until Abs(x - a) < d Return x End Function |
Рис. 4.6.2-5. Схема алгоритма и программный код процедуры Pr625(),
которая реализует ввод данных с их проверкой
Примера 4.6.2-2
Процедура- Function Pr625() может быть вызвана из любой другой процедуры или из модуля формы, например, как показано на рис. 4.6.2-4.6.
| Dim xx As Double xx = Pr625() vivodDbl1(xx, TextBox1) |
Рис. 4.6.2-6. Пример обращения к процедуре Pr625()
Примера 4.6.2-2
Пример 4.6.2-3. Задана возрастающая последовательность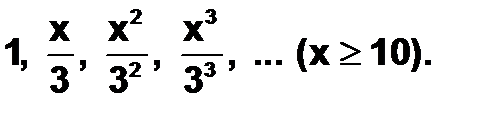 
Требуется написать программу, которая вычисляет все члены последовательности, до тех пор, пока значение очередного члена не превысит некоторое заданное число d, например, (3 <d <100).
В нашей задаче для вычисления любого члена последовательности можно воспользоваться формулой,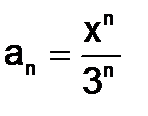 
, где n=0, 1, 2,…- номер члена.
В задачах, использующих итеративные алгоритмические структуры, рекомендуется предусмотреть так называемую «страховку от зацикливания», так как иногда условие продолжения цикла может оставаться истинным бесконечно. В данном примере цикл с постусловием будет выполняться не более 100 раз, даже если очередной член последовательности будет оставаться меньше d (рис. 4.6.2-7). Так как вывод в TextBox членов последовательности должен происходить в процессе вычисления (внутри цикла), то для решения задачи напишем процедуру- Sub.
| Sub Pr627(ByVal x As Double, _ ByVal d As Double) Dim n As Integer = 0 Dim a As Double Do а = x^n / 3^n vivodID11(n, "n=",a, "a=", TextBox3) n=n+1 Loop While a <= d And n < 100 End Sub |
Рис. 4.6.2-7. Схема алгоритма и программный код процедуры Pr627(),
которая вычисляет члены последовательности
до выполнения определенных условий
Примера 4.6.2-3
Процедура- Sub Pr627() может быть вызвана из любой другой процедуры или из модуля формы, например, как показано на рис. 4.6.2-8.
| Dim xx, dd As Double xx = vvodDbl2("Введите значение xx= ", TextBox1) dd = vvodDbl2("Введите значение dd= ", TextBox2) Pr627(xx, dd) |
Рис. 4.6.2-8. Пример обращения к процедуре Pr627()
Примера 4.6.2-3
Пример 4.6.2-4. Написать процедуру-функцию, которая вычисляет сумму членов знакопеременной убывающей последовательности с заданной точностью ε: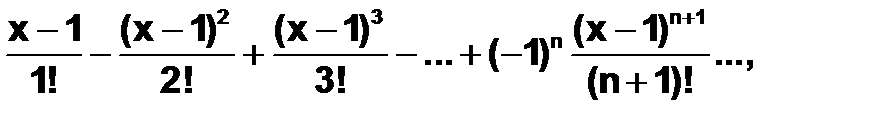 
.
Вычисление с заданной точностью ε означает, что суммирование членов ряда надо продолжать до тех пор, пока очередной вычисленный член ряда не станет меньше по абсолютной величине числа ε.
Отметим, что во многих задачах непосредственный подсчет очередного члена связан с вычислительными трудностями. В этом случае целесообразно использовать рекуррентную формулу, которая позволяет вычислить значение переменной на следующем шаге, используя ее значение на текущем шаге –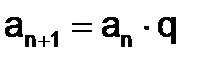 
. Выражение для q можно получить, разделив an+1 член на an член.
| Function Pr629(ByVal x As Double,_ ByVal e As Double) As Double Dim a, s As Double Dim n As Integer = 0 a = x – 1 s = 0 Do Until Abs(a) < e Or n > 100 vivodIntLs12(n, ListBox1) vivodDblLs13(a, ListBox2) s = s + a a = -a * (x - 1) / (n + 2) n = n + 1 Loop Return s End Function |
Рис. 4.6.2-9. Схема алгоритма и программный код процедуры Pr629(),
которая вычисляет сумму членов знакопеременной убывающей последовательности с точностью ε
Примера 4.6.2-4
Приведем вывод рекуррентной формулы для заданного в примере ряда. Формула для n-го члена приведена в задании:
Приведем вывод рекуррентной формулы для заданного в примере ряда. Формула для n-го члена приведена в задании:
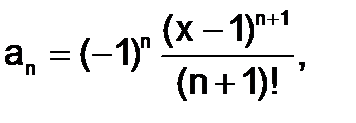тогда формула n+1 члена
Разделив an+1 член на an, получим выражение для q
Таким образом, рекуррентная формула для данного ряда:
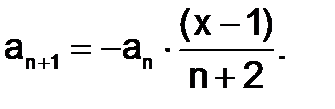
Выбор начального значения номера члена ряда (n) для нашего случая будет n=0, так как при подстановке этого значения в формулу n-го члена ряда
мы получим значение первого члена, равного x-1 или a0=x-1.
Схема алгоритма и процедура- Function приведены на рис. 4.6.2-9, причем алгоритм этот с предусловием, в котором предусмотрено выполнение цикла не более 100 раз, чтобы избежать зацикливания.
Процедура-Function Pr629() может быть вызвана из любой другой процедуры или из модуля формы, например, как показано на рис. 4.6.2-10.
| Dim xx, ee, ss As Double xx=vvodDbl2("Введите значение xx=", TextBox1) ee=vvodDbl2("Введите значение ee=", TextBox2) ss = Pr629(xx, ee) vivodDbl1(ss, TextBox3) |
Рис. 4.6.2-10. Пример обращения к процедуре Pr629()
Примера 4.6.2-4
Приведем вывод рекуррентной формулы для заданного в примере ряда. Формула для n-го члена приведена в задании:
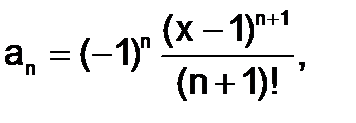тогда формула n+1 члена
Разделив an+1 член на an, получим выражение для q
Таким образом, рекуррентная формула для данного ряда:
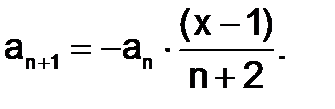
Выбор начального значения номера члена ряда (n) для нашего случая будет n=0, так как при подстановке этого значения в формулу n-го члена ряда
мы получим значение первого члена, равного x-1 или a0=x-1.
| Function P6211(ByVal x Double, _ ByVal e As Double) As Double Dim a, s As Double Dim n As Integer = 0 a = x – 1 s = 0 Do Until Abs(a) < e Or n > 100 vivodIntLs12(n,ListBox1) vivodDblLs13(a,ListBox2) s = s + a n = n + 1 a =- a * (x - 1) / (n + 1) Loop Return s End Function |
Рис. 4.6.2-11. Схема алгоритма и программный код процедуры Pr6211(),
которая вычисляет сумму членов знакопеременной убывающей последовательности с точностью ε
Примера 4.6.2-4
Схема алгоритма и код процедуры-функции приведены на
рис. 4.6.2-11. В этом случае, в отличие от предыдущего, увеличивать n (n=n+1) следует до, а не после вычисления очередного члена ряда.
