Тема 4.6
Алгоритмы итеративных циклических структур
Средства программирования итеративных циклических структур
Базовые алгоритмы итеративных циклических структур и примеры их программирования
Тестовые задания
Лабораторная работа по теме Программирование алгоритмов итеративных циклических структур
Вопросы, подлежащие изучению
Общее задание на разработку проекта
Варианты индивидуальных заданий
4.6.4.4. Содержание отчёта
Первый пример выполнения задания
Второй пример выполнения задания
Контрольные вопросы
Средства программирования итеративных циклических структур
Напомним, что циклическая структура, в которой число повторений цикла заранее неизвестно, а определяется только в процессе выполнения алгоритма, называется итеративной циклической структурой.
В зависимости от места расположения условия продолжения цикла (или выхода из цикла) итеративные циклические структуры подразделяются на два вида: с предусловием и с постусловием (рис. В.3-10 и рис. В.3-11).
При организации цикла с предусловием блоки тела цикла, следующие за блоком, в котором проверяется условие выхода из цикла, выполняются всякий раз, когда логическое выражение L принимает значение True. При первом невыполнении этого условия происходит выход из цикла. Таким образом, возможен случай, когда тело цикла не будет выполнено ни разу. Поэтому циклические структуры с известным числом повторений (регулярные циклы) относятся к числу циклических алгоритмов с предусловием.
При организации циклов с постусловием, для которых условие выхода из цикла (или повторения тела цикла) проверяется после выполнения цикла, цикл всегда выполняется хотя бы один раз, независимо от значения L, и только после его выполнения принимается решение – продолжать выполнение цикла или выйти из него.
Необходимо отметить, что логическое выражение (условие) L имеет тот же смысл, что и в Теме 4. 4.
При вычислении значений функций или каких-либо числовых последовательностей (например, арифметической прогрессии), их часто записывают в виде специальных сумм, называемых рядами. Многие числа, функции, алгоритмы численных методов могут быть записаны с помощью рядов или итерационных алгоритмов, которые позволяют вычислять их приближенные значения с заданной точностью. При программировании таких задач используются итерационные методы для организации цикла, в котором производится вычисление некоторой рекуррентной формулы.
Рекуррентная формула – это такая формула, которая сводит вычисления n -го члена последовательности к вычислению нескольких предыдущих членов (или, часто, одного предыдущего члена этой последовательности – n-1). В общем случае такая формула имеет вид:
Sn= Sn-1 + Un, где Sn – сумма первых n слагаемых ряда, которая образуется из суммы, полученной на предыдущем шаге Sn-1 и слагаемого Un, полученного на текущем шаге.
Многие числа и функции можно записать с помощью рядов, например, для числа  ряд можно записать двумя способами:
ряд можно записать двумя способами:

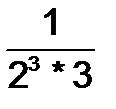 +
+ 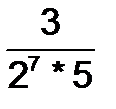 +
+  +...
+...
 = 1 −
= 1 − 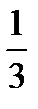 +
+  −
−  +...
+...
Второй ряд сходится более медленно, т.е. требует большего числа слагаемых для достижения той же точности.
Конструкции, реализующие в VBитеративные циклы с предусловием, могут иметь следующие форматы:
| Do While L Операторы Тела Цикла [ Exit Do ]Loop | Do Until L Операторы Тела Цикла [ Exit Do ]Loop |
А итеративные циклы с постусловием, имеют следующие форматы:
| Do Операторы Тела Цикла [ Exit Do ]Loop While L | Do Операторы Тела Цикла [ Exit Do ]Loop Until L |
Другими словами, циклы Do…Loop различаются местом расположения условия, которое помещается либо в заголовке цикла (в первой строке Do…), либо в конце цикла (в последней строке Loop…).
Для досрочного выхода из цикла используется оператор Exit Do.
Пример 4.6.1-1. Написать процедуру-Function, которая вычисляет произведение натуральных чисел от 1 до n (факториал n!=1*2*3*4*…n).
В принципе такая задача решается с помощью регулярной алгоритмической структуры (Пример 4.5.2-5). Здесь этот пример представлен в учебных целях.
| Function Pr611(ByVal n As Integer) As Long Dim I As Integer, p As Long p = 1: I = 0 Do While I < n I = I + 1: p = p * I Loop Return p End Function |
Рис. 4.6.1-1. Программный код процедуры Pr611(),
которая вычисляет факториал n Примера 6.1-1
Процедура- Futncion Pr611(), использующая итеративную циклическую структуру с предусловием, представлена на рис. 4.6.1-1.
Цикл Do…Loop в представленной программе будет выполняться до тех пор, пока значение переменной I не достигнет значения n. Здесь логическое условие продолжения цикла (I<n), помещенное после ключевых слов Do While, позволяет проверять его перед началом выполнения первого оператора тела цикла. Если условие продолжения цикла для начальных условий истинно (т.е. равно True), то все операторы цикла будут выполнены. Потом условие I<n будет проверено снова, и так до тех пор, пока условие не станет ложным – False. После этого выполнение операторов в теле цикла будет прекращено, и программа переходит к выполнению оператора, следующего за ключевым словом Loop.
Если, например, по условиям задачи необходимо, чтобы тело цикла выполнилось, по крайней мере, один раз, то в этом случае нужно использовать вторую форму оператора Do…Loop, в которой условие помещается в конце цикла, после ключевых слов Loop While… или Loop Until….
Процедура- Function, реализующая такую структуры цикла, рассмотрена в Примере 4.6.1-2.
Пример 4.6.1-2. Написать процедуру-Function, которая вводит натуральное число n, значение которого находится на отрезке [1; 15], с проверкой ввода (т.е. должны выполняться условия n>=1 AND n<=15).
Самой удобной структурой для такой проверки будет структура цикла с постусловием Do…Loop Until. Такой цикл будет повторяться до тех пор, пока это условие равно False. Как только условие станет равно True, т.е. число попадет в границы диапазона, то цикл прекращается.
Процедура- Function Pr612() представлена на рис. 4.6.1-2.
| Function Pr612() As Integer Dim n As Integer Do n = vvodInt9("Введите n (1<n<15)", TextBox1) Loop Until n >=1 And n <= 15 Return n End Function |
Рис. 4.6.1-2. Программный код процедуры Pr612(),
которая проверяет введенное значение
Примера 4.6.1-2






