Таких линий можно нарисовать множество, причем на глаз невозможно определить, какая из них лучше подходит для описания диаграммы рассеяния?
Вы уже знакомы с методом, который позволяет совершенно точно вычислить положение прямой линии, наилучшим образом проходящей через облако точек, и составить уравнение этой линии. Это – метод наименьших квадратов. Вычисляемая с его помощью прямая линия – линия регрессии. Она характеризуется тем, что сумма квадратов расстояний от точек на диаграмме до этой линии минимальна (по сравнению со всеми возможными линиями). Таким образом, линия регрессии дает наилучшее приближенное описание линейной зависимости между двумя переменными.
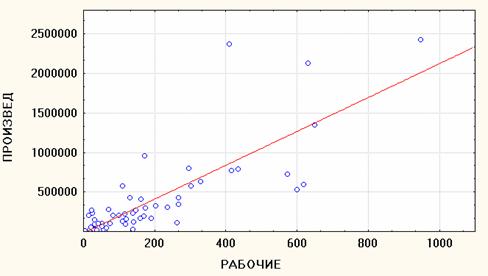
Смысл коэффициента регрессии 𝞺xy
1) В общем случае коэффициент регрессии показывает, как в среднем изменится значение Y, если X увеличится на единицу.
2) Численно он равен тангенсу угла между прямой линией регрессии Y на X и положительным направлением оси ОХ.
3) По величине коэффициента регрессии судят о силе корреляционной связи между изучаемыми величинами: чем больше величина 𝞺xy, тем сильнее изменится среднее значение Y при изменении Х, тем сильнее корреляционная связь.
Пример уравнения регрессии:
• На диаграмме рассеяния показаны не только точки-объекты и теоретическая линия регрессии, но и может быть записано уравнение этой (прямой) линии:
Y = 87610 + 2984 X
Пример интерпретации коэффициента регрессии:
• В уравнении Y = 87610 + 2984 X
коэффициент регрессии равен +2984. Что это означает?
• В данном случае смысл коэффициента регрессии состоит в том, что увеличение числа рабочих на фармацевтическом предприятии на 1 чел. приводит в среднем к увеличению объема годового производства на 2984 руб.

Какова бы ни была конфигурация облака точек на диаграмме рассеяния – лежат ли они в точности на одной прямой, или разбросаны хаотически – любая статистическая компьютерная программа всегда сможет построить уравнение регрессии. Может оказаться, что через два облака, различающихся степенью близости к линейной конфигурации, будут проведены одинаковые линии регрессии. Однако в одном случае точки могут лежать на одной прямой, а в другом случае – нет.
То есть зависимость между двумя переменными может иметь различный характер даже при одинаковых линиях регрессии.
Оказывается форма связи (линия регрессии) сама по себе не дает ответа на вопрос о тесноте связи пары переменных. На этот вопрос отвечает коэффициент парной корреляции. Он показывает, насколько тесно две переменные связаны между собой.
Визуально о тесноте связи можно судить по тому, насколько компактно расположены точки-объекты около линии регрессии. Чем ближе точки к линии регрессии, тем теснее связь.
Пример. На каком из двух графиков связь между признаками сильнее (теснее), т.е. какому из графиков соответствует более высокий коэффициент корреляции, характеризующий степень зависимости двух переменных?
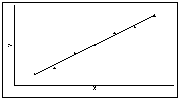
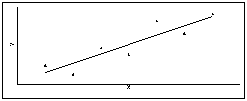
Коэффициент парной корреляции r принимает значения в диапазоне от –1 до +1.
Положительные значения коэффициента корреляции r свидетельствуют о положительной связи между признаками, отрицательные – об отрицательной связи.
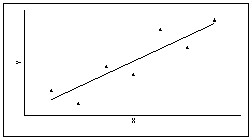

Если r = 1, то между двумя переменными существует функциональная положительная линейная связь, т.е. на диаграмме рассеяния соответствующие точки лежат на одной прямой с положительным наклоном.
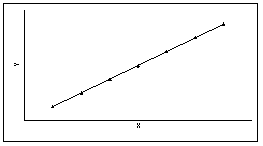
Если r = –1, то между двумя переменными существует функциональная отрицательная линейная зависимость, т.е. на диаграмме рассеяния соответствующие точки лежат на одной прямой с отрицательным наклоном.
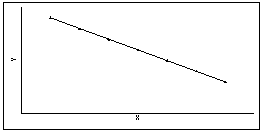
Если r = 0, то рассматриваемые переменные линейно независимы, т.е. на диаграмме рассеяния облако точек "вытянуто по горизонтали".
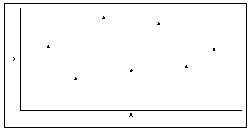
Формула для вычисления парного коэффициента корреляции:
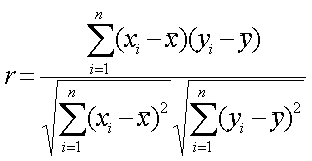
Чем выше по модулю (по абсолютной величине) значение коэффициента корреляции, тем сильнее связь между признаками. Принято считать, что коэффициенты корреляции, которые по модулю больше 0,7, говорят о сильной связи Коэффициенты корреляции, которые по модулю меньше 0,7, но больше 0,5, говорят о связи средней силы. Наконец, коэффициенты корреляции, которые по модулю меньше 0,5, говорят о слабой связи.






