ТЕМА КЛАСТЕРНЫЙ АНАЛИЗ
Вопросы: 1. Сущность кластерного анализа
Выполнение процедур кластерного анализа в пакете STATISTICA
Задание на практическое занятие.
*****************************************************************
СУЩНОСТЬ КЛАСТЕРНОГО АНАЛИЗА
Кластерный анализ (англ. cluster analysis) — многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы. Задача кластеризации относится к статистической обработке, а также к широкому классу задач обучения без учителя.
Спектр применений кластерного анализа очень широк: его используют в археологии, медицине, психологии, химии, биологии, государственном управлении,филологии, антропологии, маркетинге, социологии и других дисциплинах. Однако универсальность применения привела к появлению большого количества несовместимых терминов, методов и подходов, затрудняющих однозначное использование и непротиворечивую интерпретацию кластерного анализа.
Задачи и условия
Кластерный анализ выполняет следующие основные задачи:
· Разработка типологии или классификации.
· Исследование полезных концептуальных схем группирования объектов.
· Порождение гипотез на основе исследования данных.
· Проверка гипотез или исследования для определения, действительно ли типы (группы), выделенные тем или иным способом, присутствуют в имеющихся данных.
Независимо от предмета изучения применение кластерного анализа предполагает следующие этапы:
· Отбор выборки для кластеризации. Подразумевается, что имеет смысл кластеризовать только количественные данные.
· Определение множества переменных, по которым будут оцениваться объекты в выборке, то есть признакового пространства.
· Вычисление значений той или иной меры сходства (или различия) между объектами.
· Применение метода кластерного анализа для создания групп сходных объектов.
· Проверка достоверности результатов кластерного решения.
Типы входных данных:
· признаковое описание объектов. Каждый объект описывается набором своих характеристик, называемых признаками. Признаки могут быть числовыми или нечисловыми.
· матрица расстояний между объектами. Каждый объект описывается расстояниями до всех остальных объектов метрического пространства.
· матрица сходства между объектами. Учитывается степень сходства объекта с другими объектами выборки в метрическом пространстве. Сходство здесь дополняет расстояние (различие) между объектами до 1.
Цели кластеризации:
· понимание данных путём выявления кластерной структуры. Разбиение выборки на группы схожих объектов позволяет упростить дальнейшую обработку данных и принятия решений, применяя к каждому кластеру свой метод анализа (стратегия «разделяй и властвуй»).
· сжатие данных. Если исходная выборка избыточно большая, то можно сократить её, оставив по одному наиболее типичному представителю от каждого кластера.
· обнаружение новизны (англ. novelty detection). Выделяются нетипичные объекты, которые не удаётся присоединить ни к одному из кластеров.
В первом случае число кластеров стараются сделать поменьше. Во втором случае важнее обеспечить высокую степень сходства объектов внутри каждого кластера, а кластеров может быть сколько угодно. В третьем случае наибольший интерес представляют отдельные объекты, не вписывающиеся ни в один из кластеров.
Во всех этих случаях может применяться иерархическая кластеризация, когда крупные кластеры дробятся на более мелкие, те в свою очередь дробятся ещё мельче, и т. д. Такие задачи называются задачами таксономии. Результатом таксономии является древообразная иерархическая структура. При этом каждый объект характеризуется перечислением всех кластеров, которым он принадлежит, обычно от крупного к мелкому.
Методы кластеризации
Общепринятой классификации методов кластеризации не существует, но можно выделить ряд групп подходов (некоторые методы можно отнести сразу к нескольким группам и потому предлагается рассматривать данную типизацию как некоторое приближение к реальной классификации методов кластеризации):
1. Вероятностный подход. Предполагается, что каждый рассматриваемый объект относится к одному из k классов.
2. Подходы на основе систем искусственного интеллекта.
3. Логический подход. Построение дендрограммы осуществляется с помощью дерева решений.
4. Теоретико-графовый подход.
5. Иерархический подход. Предполагается наличие вложенных групп (кластеров различного порядка).
6. Другие методы.
Подходы 4 и 5 иногда объединяют под названием структурного или геометрического подхода, обладающего большей формализованностью понятия близости. Несмотря на значительные различия между перечисленными методами все они опираются на исходную «гипотезу компактности»: в пространстве объектов все близкие объекты должны относиться к одному кластеру, а все различные объекты соответственно должны находиться в различных кластерах.
Формальная постановка задачи кластеризации
Пусть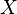 
— множество объектов, 
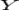— множество номеров (имён, меток) кластеров.
Задана функция расстояния между объектами 
.
Имеется конечная обучающая выборка объектов 
.
Требуется разбить выборку на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из объектов, близких по метрике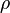 
, а объекты разных кластеров существенно отличались. При этом каждому объекту 
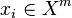приписывается номер кластера 
.
Существует около 100 разных алгоритмов кластеризации, однако, наиболее часто используемые - иерархический кластерный анализ и кластеризация методом k-средних.
