Запишемо систему (1) у розгорнутому вигляді:
(2)
Метод Гаусса розв’язання системи (2) полягає у послідовному вилученні невідомих 
з цієї системи. Вважаємо, що a11 ¹0, поділимо 1-ше р-ня на a11:
(3)
Розглянемо тепер рівняння системи (2), що залишилися
; i= 2,n. (4)
Помножимо (3) на - 
та додамо одержане рівняння до і-го рівняння системи (4), i=2,n.
У результаті одержимо наступну систему рівнянь:
. Ми отримаємо трикутну матрицю, де на k-му кроці перетворення коефіцієнти визначаються формулою 
. Виконується, коли ведучий елемент ¹0. Якщо ведучий елемент =0, тоді у рядку нижче шукають ненульовий елемент і переставляють місцями рядки.
Виконані нами дії еквівалентні множенню обох частин початкової системи зліва на елементарну трикутну матрицю вигляду:
Не важко побачити, що одне перетворення методу Гауса еквівалентне множенню системи на L1-1: 
. Нехай у нас уже оброблено і-1 стовпчик початкової матриці. Тоді матриця Lі-1 матиме вигляд: 
Продовжуючи таким чином до останнього рівняння одержимо систему з трикутною верхньою матрицею 
, де U= 
A – верхня трикутна матриця. Тобто отримаємо: 
.
Метод Гауса вимагає n3/3+О(n2) операцій додавання і віднімання і стільки ж операцій множення і ділення.
Ітераційне уточнення одержаного розв’язку:
Уточнення не треба, якщо y має порядок похибки округлення.
II Метод віддзеркалення.
Цей метод базується на розкладі матриці СЛАР (сис-ми лін. алгебраїчних рівнянь) на добуток ортогональної і верхньої трикутної матриці. A=QR, де Q – ортогональна матриця, яка є добутком елементарних ортогональних матриць, так званих матриць віддзеркалення або перетворень Хаусхолдера. Цей метод вимагає вдвічі більше операцій, ніж метод Гауса.
III Для специфічних матриць:
1) Якщо матриця симетрична, то метод квадратного кореня використовує в 2 рази менше часу, ніж метод Гауса. A - симетрична, A=LLT, L - нижня, LT- верхня трикутна матриця.
Звідси 
, і взагалі, 
, 
. Цей метод має недоліки, якщо в системі присутні дійсні коефіцієнти (при розрахунках на ПЕОМ).
2) Матриця A (система рівнянь з цією матрицею) має тридіагональний вигляд:
В цьому випадку для роз-ку задачі використовується метод прогонки, який вимагає порядку 8 n операцій. Якщо здійснити розщеплення, то можна очікувати, що вони дводіагональні, отже існує зв’язок 
, тоді 
. Цей вираз підставимо в і-те рівняння. Для визначення покрокових a і b ми маємо перше рівняння 
. Метод визначення a і b називається прямим ходом прогонки. Якщо відоме останнє xn, то зворотнім ходом можна визначити всі xn-1,..,x1. А xn ми оберемо з останнього рівняння 
. Метод прогонки потребує O(n).
Ітераційні методи
Багато практично важливих задач зводяться до роз-ня СЛАР дуже великої розмірності, матриці яких не є щільно заповненими (містять багато нульових елементів). У цьому випадку вигідно застосовувати ітераційні методи. Розглянемо систему 
. Ітераційні методи складаються з перетворень цієї системи до еквівалентної: 
та організації обчислювального процесу 
при заданому початковому наближенні 
. За таких умов процес 
буде збігатися до дійсного розв’язку системи. Розглянемо послідовність 
, 
і т.д., де 
,..., та зрозуміло 
У нас для оптимального розв’язку послідовність 
повинна бути скінченою. Для цього необхідно 
, а тоді 
приймає вигляд 
. Існує декілька підходів для отримання цього з 
. Розглянемо ці підходи:
1. Метод Якобі. Вважаємо, що a11¹0, тоді 
,..., 
. (*)
Визначимо ітерації формулами: 
Якщо задати вектор 
, то можна сподіватися, що при 
. Цей метод носить назву методу Якобі. Як і для багатьох ітераційних методів для цього методу існує 2 критерії припинення процесу: 1) кількість ітерацій досягає верхньої критичної межі; 2) виконується умова досягнення потрібної точності. Такою умовою може бути: 
.
3. Методи інтерполювання. Множники Лагранжа та Ерміта. Сплайни.
Задача наближення функцій виникає при розв’язанні багатьох задач (обробка експериментальних даних, чисельне диференціювання та інтегрування функцій, розв’язання диференціальних та інтегральних рівнянь).
Дуже зручною у використанні на практиці функцією є многочлен. Щоб задати многочлен, треба задати тільки скінчену кількість його коефіцієнтів. Значення многочлена просто обчислюються, його легко продиференціювати, проінтегрувати і т.д. Тому алгебраїчні многочлени знайшли широке застосування для наближення (апроксимації) функцій.
Постановка задачі інтерполяції. Нехай відомі значення деякої функції 
у 
різних точках 
які позначимо 
Виникає задача поновлення
(наближеного) функції у довільній точці 
.
Іноді відомо, що наближену функцію доцільно шукати у вигляді
де вигляд функції 
відомий, а параметри 
треба визначити.
Коли параметри визначаються з умови збігу 
і наближеної функції 
у точках тобто 
то такий спосіб наближення називається інтерполяцією. Точки 
називаються вузлами інтерполяції.
Серед способів інтерполяції найбільш поширеним є випадок лінійної інтерполяції.
де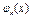 
- деякі відомі функції. Значення коефіцієнтів 
визначаються з умови збігу з вихідною функцією у вузлах інтерполяції
(1)
тобто з системи n +1 лінійних рівнянь з n+1 невідомими 
Достатня умова існування єдиного роз-ку сис-ми для довільного набору вузлів є вимоги, щоб ф-ція 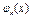була ф-цією Чебешова: 
. Тоді отримаємо 
(2)
тобто інтерполяція здійснюється многочленом, який називається інтерполяційним.
Теорема. Якщо вузли интерполяції різні, то існує єдиний інтерполяційний многочлен n- го ступеню.
В загальному вигляді 
, (3)
(4)
Інтерполяційний многочлен, представлений у вигляді (3), називається інтерполяційним многочленом Лагранжа, а функції (коефіцієнти) (4) - Лагранжевими коефіцієнтами. Існують також інші форми запису інтерполяційного многчлену, але за наведеною теоремою інтерполяційний многочлен n-го степеня – єдиний.
Завжди можна записати рівність 
, де 
- залишковий член, тобто похибка інтерполювання. шукають у вигляді 
, де 
, а rn(x) - деяка функція, значення якої у вузлах інтерполяції xi можна задавати які завгодно, оскільки 
. Оцінка похибки інтерполяції в поточній точці xÎ [a,b] має вигляд 
, де const M дорівнює 
.
Лінійна інтерполяція.
Інтерполяція за формулою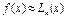 
при n=1, тобто за допомогою лінійної функції 
, називається лінійною. Якщо ввести позначення 
, 
то формула лінійної інтерполяції запишеться у вигляді 
, де q називається фазою інтерполяції, яка змінюється від 0 до 1, коли x пробігає значення від x0 до x1.
Многочлени Чебишева.
Для того, щоб максимальна похибка інтерполяції функції f на відрізку [a,b] (
) була мінімальною, в якості вузлів інтерполяції беруть корені многочлена Чебишева Tn+1(x): 
. Ці точки 
є оптимальними вузлами оцінки похибки інтерполяції на відрізку [a,b]. Оцінка похибки має вигляд 
, де 
.
Інтерполяція з рівновіддаленими вузлами.
Якщо відрізок [a,b] великий і необхідна висока точність апроксимації функції, то часто користуються таблицею значень функції у вузлах, що розбивають відрізок з постійним кроком, число їх може бути достатньо великим. Нехай 
- вузли інтерполяції, h>0 - крок, причому 
. Позначимо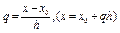 
, тоді інтерполяційний многочлен буде мати вигляд 
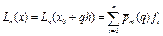, де 
. Залишковий член (похибка інтерполяції) має вигляд 
, де 
- n+1 похідна по x, 
- деяка проміжна точка, 
.
Інтерполювання з кратними вузлами.
Побудувати многочлен 
степеня m такий, що 
. Многочлен називається інтерполяційним многочленом Ерміта.
Нехай при таких умовах 
; 
– многочлен Ерміта.
Сплайни.
Перевагою сплайнів над звичайною інтерполяцією є, по-перше, їх збіжність, і, по-друге, стійкість процесу обчислень.
Інтерполювання сплайном полягає в наступному: область визначення функції D(u) ділять на частини Dі, 
, які не перетинаються між собою і для яких 
, в кожній частині ф-ція визначається як поліном і називається сплайн-функцією.
На відрізку [a,b] визначимо сітку 
, по вузлах якої задане значення функції. Назвемо сплайном 
функцію, яка є поліномом степеня m на кожному проміжку 
з сіткою ∆, в вузлах хі приймає значення 
і має в цих вузлах неперервні похідні до порядку k включно. m – це порядок сплайну, m-k – це дефект сплайну. На практиці найбільш широке розповсюдження отримали сплайни третього степеня. Ці сплайни називаються кубічними і позначаються S3(x).
Озн. Кубічним сплайном називається функція, яка має такі властивості:
а) на кожному сегменті 
функція 
є поліномом третього степені;
б) функція , а також її перша і друга похідні неперервні на 
;
в) 
;
г) 
.8
Озн. Умова в) називається умовою інтерполювання.
Озн. Сплайни, які задовольняють умову г) називаються природніми.
Озн. Величина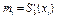 
називається нахилом сплайну в точці (вузлі) xi.
Отже, щоб задати кубічний сплайн S3(x) на всьому відрізку [a,b], необхідно задати в N+1 узлах xi його значення fi та нахили mi, i=0,...,N. Нахили можна задати, наприклад, так: 
, 
, причому 
, 
, h=(b-a)/N.
4. Методи чисельного інтегрування.
Розглянемо методи наближеного знаходження визначених інтегралів 
, що засновані на заміні інтегралу кінцевою сумою 
, де 
- числові коефіцієнти, 
- точки відрізку [a,b], k = 0,1,..,n. Для знаходження таких інтегралів використовуються квадратурні формули інтерполяційного типу 
(*).
- квадратурна сума, - вузли квадратурної формули, - коефіцієнти квадратурної формули. Різниця 
- похибка квадратурної формули, залежить як від розташування вузлів, так і від вибору коефіцієнтів.
Нехай має місце (*), а коефіцієнт будемо шукати з умови точності цієї формули для поліномів вищого степеня. Розглянуті нами формули називаються формулами з фіксованими вузлами інтегрування. Якщо ж вузли інтегрування заздалегідь не визначати, то можна намагатися одержати квадратурну формулу точну для поліномів 2n+1 степеня. Такі формули, де зафіксовані і вагові коефіцієнти і вузли називаються формулами найвищого алгебраїчного степеня точності або формулами типу Гауса. Але щоб одержати всі невідомі, треба розв’язувати нелінійну систему рівнянь або систему нелінійних рівнянь.
Теорема чисельного інтегрування:
Нехай 
на [a,b]. Тоді 
таке, що 
Розглянемо такі квадратурні формули:
a) формула прямокутників с залишковим членом
, 
б) формула трапецій с залишковим членом
, 
в) Формула Сімпсона (формула парабол)
, 
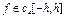
Вище розглянуті квадратурні формули - канонічні. Можна побудувати ускладнені формули на [a,b]: відрізок [a,b] ділимо на N частин, до кожної застосували якусь канонічну квадратурну формулу і сумують результати. Так виведемо ускладнену квадратурну формулу прямокутників:
часткові відрізки: 
,
i=0,1,..,N-1, 
, h=(b-a)/N
- значення f
в середині відрізку 
, при цьому
, 
- деяка точка
скадаючи отримаємо ускладнену квадратурну формулу.
, - точка [a,b]
ускладнена квадратурна формула з залишковим членом.
5. Чисельні методи розв’язання задачі Коші.
Розглянемо диференційне рівняння першого порядку:
(1).
Задача Коші полягає в наступному: знайти розв’язок u(x) рівняння , що задовольняє початкову умову 
(2). Функція u(x) може бути як скалярною, так і векторною.
Загальний вигляд задачі Коші для n-го порядку звичайних диференційних рівнянь має вигляд:
(3). Для такої задачі початкові умови записуються так: 
(4). Вони дозволяють виділити з мн-ни роз-ків єдиний роз-к:
.
Всі методи розв’язання задачі Коші діляться на 2 типа: 1) точні; 2) наближені. В свою чергу наближені поділяються на 2 типи: 1) аналітичні; 2) чисельні.
В аналітичних методах роз-к будується як послідовність функцій 
. Перевага цього роз-ку в тому, що він у вигляді функції. До аналітичних методів належать такі методи як метод послідовних наближень та метод степеневих рядів.
Чисельні методи дають роз-к лише на деякій мн-ні точок, тобто у вигляді таблиці. Ці значення теж будуть наближеними. Чисельні методи бувають однокрокові та багатокроккові. В однокрокових методах для знаходження роз-ку в якійсь точці використовується лише інформація в попередній точці. В бгатокрокових методах для знаходження роз-ку в якійсь точці використовується інформація в декількох попередніх точках.
Розглянемо деякі чисельні методи роз-ня задачі Коші.
. Якщо використати це рівняння то можемо написати: 
(5). Отже, якщо у нас було відоме 
, то ми зможемо знайти 
. Введемо сітку: 
. Тоді роз-к задачі (1), (2) на цій сітці можна одержати з (5) шляхом заміни інтеграла деякою квадратурною формулою:
Метод Ейлера
Замінимо інтеграл квадратурною формулою лівих прямокутників. Одержимо 
(6) – формула Ейлера.
