Площадь поперечного сечения
 см2.
см2.
Статический момент площади относительно оси 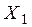
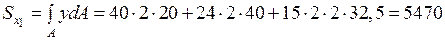 см3.
см3.
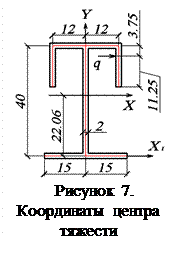 Координаты центра тяжести (рис. 7)
Координаты центра тяжести (рис. 7)
 см;
см;
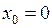 см.
см.
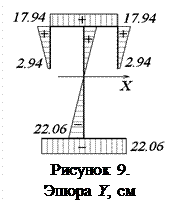
Моменты инерции относительно центральных осей (вычисляются при помощи эпюр линейных координат рис. 8 и 9)
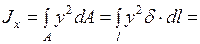
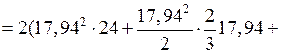
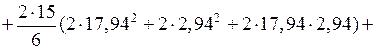
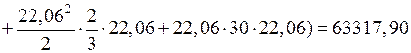 см4;
см4;
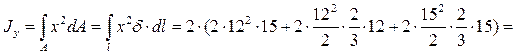 15444 см4.
15444 см4.

3.1.3. Определение координат центра изгиба
Для определения центра изгиба строим эпюру секториальных координат (рис. 10) с произвольным полюсом В и началом отсчета 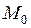 . Точки B и
. Точки B и 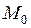 располагаем на контуре по оси симметрии сечения.
располагаем на контуре по оси симметрии сечения.
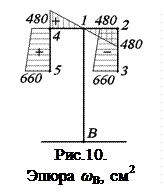 Секториальную координату определяем по формуле
Секториальную координату определяем по формуле
 .
.
 см2;
см2; 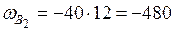 см2;
см2;
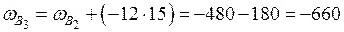 см2;
см2; 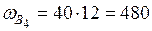 см2;
см2;
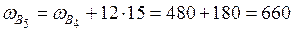 см2.
см2.
Секториально-линейный статический момент относительно оси Y вычисляем перемножением эпюр 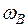 и X по формуле
и X по формуле
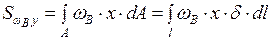 .
.
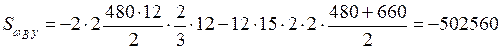 см5.
см5.
Определяем координаты центра изгиба
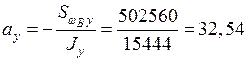 см,
см,
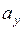 откладываем от полюса B по оси Y, получаем центр изгиба А
откладываем от полюса B по оси Y, получаем центр изгиба А
(рис. 11).
 3.1.4. Построение эпюры главных секториальных координат поперечного сечения
3.1.4. Построение эпюры главных секториальных координат поперечного сечения
 см2;
см2; 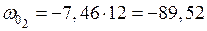 см2;
см2;
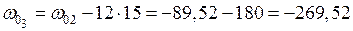 см2;
см2;
 см2;
см2; 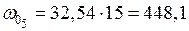 см2;
см2;
 см2;
см2;
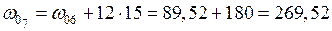 см2;
см2;
 см2.
см2.
Проверка правильности определения положения центра изгиба:
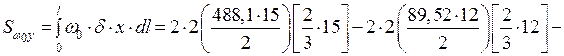
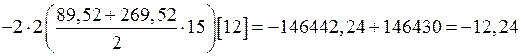 см5.
см5.
 .
.
Эпюра 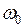 построена правильно, положение центра изгиба верное.
построена правильно, положение центра изгиба верное.
3.1.5. Вычисление момента инерции при чистом кручении 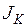 ,
,
секториального момента инерции 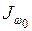 , изгибно-крутильной
, изгибно-крутильной
Характеристики K
 .
.
Для двутаврового сечения  .
.
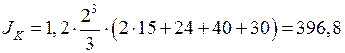 см4
см4  м4;
м4;

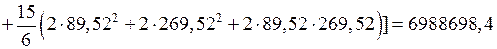 см6;
см6;
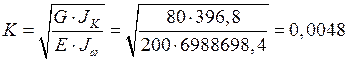 см-1
см-1 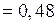 м-1.
м-1.
Определение неизвестных начальных параметров

На рис.12 показан эксцентриситет е.
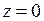 ;
; 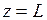 ;
;
 ;
; 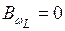 ;
;
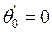 ;
;  .
.
 ;
;
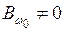 .
.
 ,
,
где  см;
см;
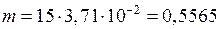 кН·м/м;
кН·м/м;
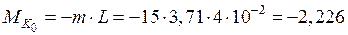 кН·м.
кН·м.
При 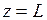 по табл. 5
по табл. 5
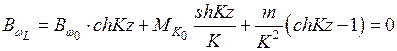 ;
;
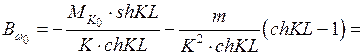
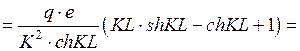
 кН·м2.
кН·м2.
Определение ординат для построения
эпюры бимоментов 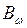
По табл. 5
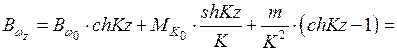
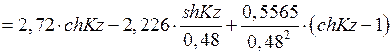 .
.
С шагом в 1 м длины балки определяем
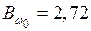 кН·м2;
кН·м2;
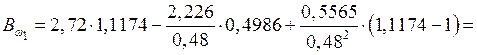
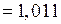 кН·м2;
кН·м2;
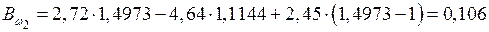 кН·м2;
кН·м2;
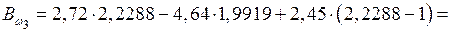
 кН·м2;
кН·м2;
 кН·м2.
кН·м2.
Определение ординат для построения эпюры
изгибно-крутящих моментов 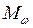
По табл. 5
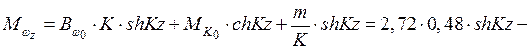
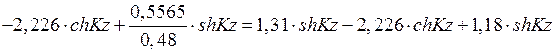 ;
;
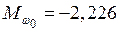 кН·м;
кН·м;
 кН·м;
кН·м;
 кН·м;
кН·м;
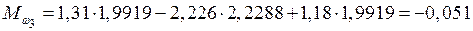 кН·м;
кН·м;
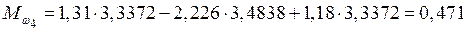 кН·м.
кН·м.
Определение ординат для построения эпюры
моментов чистого кручения 
По табл.5
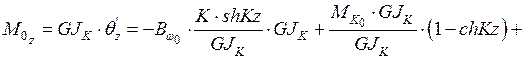
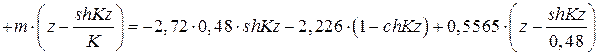 ;
;
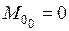 ;
;
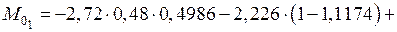
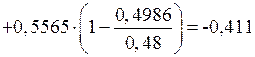 кН·м;
кН·м;
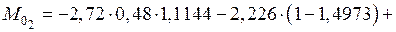
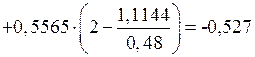 кН·м;
кН·м;

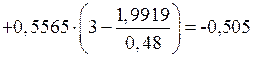 кН·м;
кН·м;
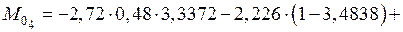
 кН·м.
кН·м.
Определение ординат для построения эпюры
внешних крутящих моментов 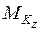
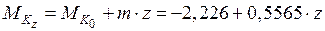 ;
;
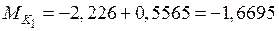 кН·м;
кН·м;
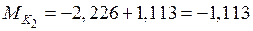 кН·м;
кН·м;
 кН·м;
кН·м;
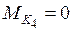 .
.
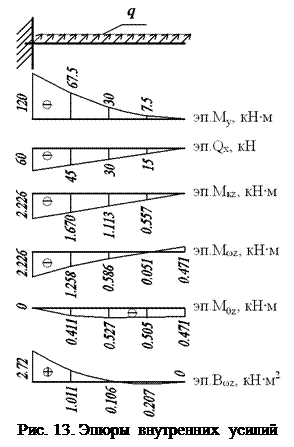
Результаты вычислений внутренних усилий сводим в табл.8.
Таблица 8
Внутренние усилия
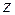
| 
| 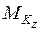
| 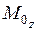
| 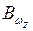
| 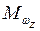
| shKz | chKz |
| -2,226 | 2,72 | -2,226 | |||||
| 0,48 | -1,6695 | -0,411 | 1,011 | -1,258 | 0,4986 | 1,1174 | |
| 0,96 | -1,113 | -0,527 | 0,106 | -0,586 | 1,1144 | 1,4973 | |
| 1,44 | -0,5565 | -0,505 | -0,207 | -0,051 | 1,9919 | 2,2288 | |
| 1,92 | -0,471 | 0,471 | 3,3372 | 3,4838 |
3.1.11. Построение эпюр внутренних усилий 
Эпюры внутренних усилий, построенные по данным табл. 8, показаны на рис. 13.
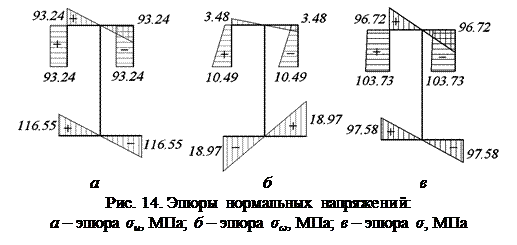
Построение эпюры нормальных напряжений
В опасном сечении стержня
Нормальные напряжения
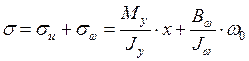 .
.
По эпюрам 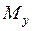 и
и 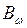 опасным сечением в консольной балке является опорное.
опасным сечением в консольной балке является опорное.
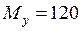 кН·м
кН·м 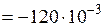 МН·м;
МН·м;
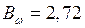 кН·м2
кН·м2 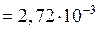 МН·м2;
МН·м2;
 (рис. 14, а);
(рис. 14, а);
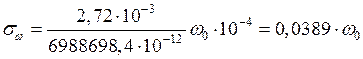 (рис. 14, б).
(рис. 14, б).
Эпюры 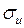 и
и  построены с помощью эпюр X и
построены с помощью эпюр X и 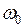 . Эпюру
. Эпюру 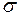 получаем суммированием эпюр
получаем суммированием эпюр 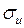 и
и  (рис. 14, в).
(рис. 14, в).
Построение эпюр касательных напряжений
В опасном сечении стержня
Касательные напряжения
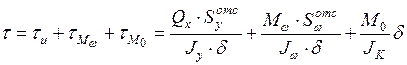 .
.
По эпюрам  опасным является опорное сечение.
опасным является опорное сечение.
Касательные напряжения от изгиба
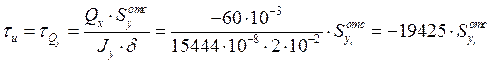 ,
,
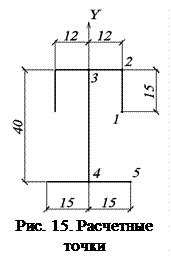 где
где  – статический момент отсеченной части сечения относительно оси Y.
– статический момент отсеченной части сечения относительно оси Y.  считается с помощью рис. 15.
считается с помощью рис. 15.
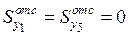 ;
;
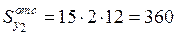 см3
см3 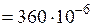 м3;
м3;
 см3
см3 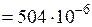 м3;
м3;
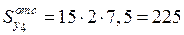 см3
см3 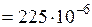 м3.
м3.
Остальные участки симметричны найденным.
 Касательные напряжения от изгиба (рис. 16)
Касательные напряжения от изгиба (рис. 16)
 ;
;
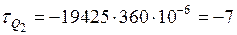 МПа;
МПа;
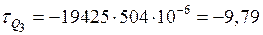 МПа;
МПа;
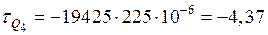 МПа.
МПа.
Определяем напряжения от изгибно-крутящего момента.
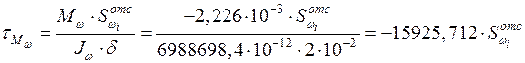 .
.
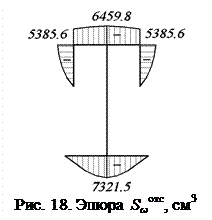
Эпюра  (рис. 18) строится с помощью эпюры
(рис. 18) строится с помощью эпюры 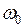 (рис. 17).
(рис. 17).

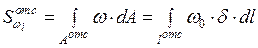 ;
;
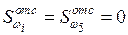 ;
;
 см4;
см4;
 см4;
см4;
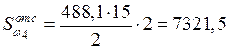 см4.
см4.
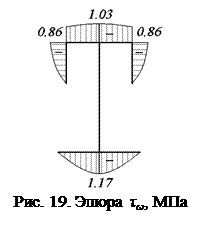
Касательные напряжения от изгибно-крутящего момента (рис. 19)
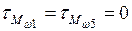 МПа;
МПа; 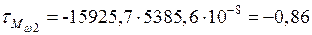 МПа;
МПа;
 МПа;
МПа;
 МПа.
МПа.
 Находим напряжения от чистого кручения
Находим напряжения от чистого кручения
в опорном сечении 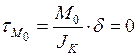 , так как в опорном сечении
, так как в опорном сечении  .
.
Эпюру 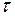 получаем суммированием эпюр
получаем суммированием эпюр 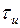 ,
, 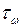 и
и  (рис.20).
(рис.20).
3.1.14. Нахождение угла закручивания
При 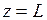
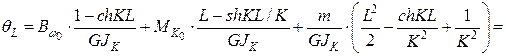
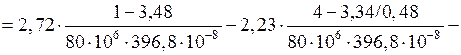
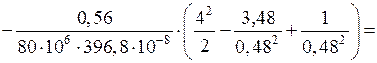
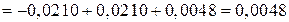 рад.
рад.
Пример №2
Исходные данные
Таблица 9
Исходные данные
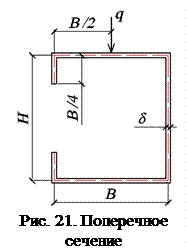
| В, см | |
| Н, см | |
| δ, см | 1,6 |
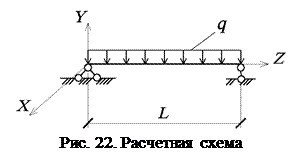
| q, кН/м | |
| L, м | |
| Е, ГПа | |
| G, ГПа |
В табл. 9 приведены исходные данные для примера №2. На рис. 21 и 22 даны поперечное сечение и расчетная схема рассматриваемого стержня.