М-метод применяется для решения любых задач ЛП, в том числе и тех, где начальное базисное решение сразу не определяется. М-метод состоит во введении новых искусственных переменных, которые сразу можно взять в качестве базисных, и дальнейшем решении полученной задачи симплекс-методом.
Исходная ЗЛП в канонической форме: F(X) = c1Х1 +... + сnXn => max
ai,1X1 +... + ai,nXn = bi, (i=1,m) Xj>0, (j=1,n)
Алгоритм М-метода:
В каждое i-ое ограничение вводим искусственную переменную Xn+i >0. Всего m новых искусственных переменных.
В целевую функцию F вводим m дополнительных отрицательных слагаемых вида:
-M*Xn+1 -M*Xn+2...-M*Xn+m, где М - произвольная очень большая константа.
Получим новую ЗЛП вида: F(X) = c1Х1 +... + сnXn -M*Xn+1 -... -M*Xn+m => max
ai,1X1+... + ai,nXn +Xn+i = bi, (i=1,m) Xj >0, (j=1,n+m)
Новая система ограничений характерна тем, что искусственные переменные сразу можно взять в качестве базисных: Xn+i = bi - ai,1X1 -... - ai,nXn, (i=1,m)
Формируем начальное базисное решение новой М-задачи: X' = (0,... 0, b1,... bm)
Решаем М-задачу симплекс-методом
Анализируем решение М-задачи в соответствии со следующими правилами:
Если в оптимальном решении М-задачи: X" = (X"1,... X"n, X"n+1,... X"n+m)
все искусственные переменные равны 0, то вектор X" = (X"1,... X"n)
является оптимальным решением исходной ЗЛП.
Если в оптимальном решении М-задачи хотя бы одна искусственная переменная не равна 0, то исходная ЗЛП не имеет решения в силу несовместимости ограничений.
Если М-задача не имеет решения, то исходная ЗЛП также не имеет решения в силу неограниченности целевой функции на допустимом множестве.
15. Транспортная задача. Постановка задачи и её математическая модель.
Транспортная задача — одна из распространенных задач линейного программирования. Ее цель — разработка наиболее рациональных путей и способов транспортирования товаров, устранение чрезмерно дальних, встречных, повторных перевозок.
Постановка транспортной задачи.Важным частным случаем задачи линейного программирования является транспортная задача.Постановка задачи: Пусть имеется m поставщиков и n потребителей. Мощность поставщиков и спросы потребителей, а так же затраты на перевозку груза для каждой пары «поставщик – потребитель» заданы таблицей.
Математическая модель транспортной задачи.
Пусть хij – количество груза, перевозимого с i-го в j-й пункт. Целевая функция: 
Система ограничений:
Для решения задачи составляется таблица. В клетки таблицы записывается стоимость соответствующих перевозок сij и в них же заносятся значения перевозок xij, удовлетворяющих поставленным ограничениям. Клетки с не нулевыми перевозками называются базисными, а с нулевыми – свободными. В зависимости от соотношения между запасами и заявками транспортная задача называется сбалансированной или несбалансированной.
Сбалансированная ТЗ: 
Несбалансированная ТЗ: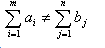 
Для сбалансированной ТЗ ограничения принимают вид равенств, то есть получаем m+n ограничений, в которых все переменные линейно зависимы. В результате допустимое решение сбалансированной ТЗ может быть получено, если заполнять клетки транспортной таблицы таким образом, чтобы сумма перевозок в каждой строке 
должна быть равна запасам ai, а сумма перевозок в каждом столбце равна соответствующей заявке вj. Вариантов заполнения транспортной таблицы множество, поэтому искомым решением является то из допустимых решений, для которых общая стоимость перевозок будет минимальной.
