Математическое моделирование экономических задач. его этапы.
Целью математического моделирования экономических систем является использование методов математики для наиболее эффективного решения задач, возникающих в в сфере экономики, с использование, как правило, современной вычислительной техники.
Процесс решения экономических задач осуществляется в несколько этапов:
Содержательная (экономическая) постановка задачи. Вначале нужно осознать задачу, четко сформулировать ее. При этом определяются также объекты, которые относятся к решаемой задаче, а также ситуация, которую нужно реализовать в результате ее решения.
Следующим этапом является математическая постановка задачи, в процессе которой осуществляется построение математической модели объекта и определение методов (алгоритмов) получения решения задачи. Это - этап системного синтеза (математической постановки) задачи. Следующим этапом является разработка программы решения задачи на ЭВМ. Для сложных объектов, состоящих из большого числа элементов, обладающих большим числом свойств, может потребоваться составление базы данных и средств работы с ней, методов извлечения данных, нужных для расчетов.
На заключительном этапе производится эксплуатация модели и получение результатов.
Таким образом, решение задачи включает следующие этапы:
1. Содержательная постановка задачи.
2. Системный анализ.
3. Системный синтез (математическая постановка задачи)
4. Разработка или выбор програмного обеспечения.
5. Решение задачи.
Общая задача линейного программирования.
Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции
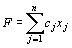стремится к(max, min) ͢при условиях 
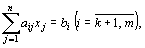
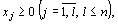где - 
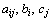заданные постоянные величины и 
.
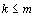Матричная форма записи ЛП.
Обозначим С (с1, с2,…сn)- матрица-строка коэф-ов при неизвестных в фун. f, матрица сост из ограничений
с =(
… 
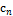) - вектор-строка коэффициентов целевой функции;
x=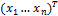 
- вектор-столбец неизвестных;
b = (bl...,bm)T - вектор-столбец правых частей ограничений; и матрицу коэффициентов задачи:
А =││ 
││
Тогда ЗЛП в матричном виде запишется так:
Задача об использ рес имеет вид:
f = CX→мах; АX ≤ B; х≥0.
Задача о смесях: f = CX→min; АX 
B; х≥0. Cущ-т задачи: f = CX→max(min); АX 
B; х≥0.
4.Задачи ЛП:задача о распределении ресурсов.
Задача об использовании ресурсов в общем виде:
Предприятие выпускает n видов продукции с использованием m видов огранич рес. Известны: bi (i=1,2…m)-запас рес i-го вида; aij (i=1,2…m, j=1,2…n)-кол рес i-го вида, идущего на изготовление единицы продукции j-го вида;
Сj (j=1,2…n)- дох от реализации единицы продукции j-го вида.Сост такой план выпуска продукции, чтоб при ее реализации получ max дох. Обозначим: xj(j=1,2..n)-кол продукции j-го вида. Задача может быть описана моделью:
F=c1x1+c2x2+…+cnxnàmax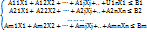 
Xj 
0 (j=1,2..n)
5.Задача о диете в общем виде:
Имеется n видов кормов. В каждой порции смеси содержат m питательных веществ в количествах не менее bi (i=1,2…m). Известно: aij (i=1,2…m, j=1,2…n)- количество i –го питательного вещества, содержащегося в единице корма j –го вида. Cj (j=1,2…n)- стоимость единицы корма j-го вида. Надо: смешать имеющиеся корма так, чтоб обеспечить заданную питательность при min затратах на корма. Обозначим: xj (j= 1,2…n)-кол-во корма j-го вида. Модель: f=c1x1+c2x2+…cnxn-->min.
xj 0 (j=1,2…n)
Двойственная задача ЛП
Двойственная задача - вспомогательная зад. Л.П., получаемая с помощью определенных правил из целевой исходной зад.
1. Если исход является задачей максимизации, то двойственная будет задачей минимизаци, и наоборот.
2. Коэффициенты целевой функции исход задачи c1, …,cn становятся свободными членами ограничений двойственной задачи.
3. Свободные члены ограничений исход задачи b1, …,bm становятся коэффициентами целевой функции двойственной задачи.
4. Матрица ограничений двойственной задачи получается путем транспортирования матрицы ограничений исход задачи.
5. Знаки неравенств в ограничениях изменяются на противоположные.
6. Число ограничений исход задачи равно числу переменных двойственной задачи, и наоборот.
