Дифференциальное уравнение есть

общий вид дифференциального уравнения первого порядка

Дифференциальное уравнение 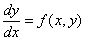есть дифференциальное уравнение первого порядка, разрешенное относительно ___________

производной

Дифференциальное уравнение 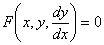есть общий вид дифференциального уравнения _________ порядка (ответ дать словом)

первого

Для 2-х моторов вероятность безотказной работы в течение дня равнаp¹= 0.9 иp²=0.75 соответственно. Какова вероятность безотказной роботы в течении дня 2-х моторов?

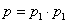, р = 0.675

Для 2-х моторов вероятность безотказной работы в течение дня равнаp¹= 0.9 иp²=0.75 соответственно. Какова вероятность того, что в течение дня оба мотора сломаются?

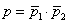, р = 0.025

Для 2-х моторов вероятность безотказной работы в течении дня равнаp¹= 0.9 иp²=0.75 соответственно. Какова вероятность безотказной роботы в течение дня хотя бы 1-го мотора?

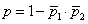, р = 0.975

Для биномиального распределения выражение 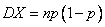определяет его ___________

дисперсию

Для биномиального распределения выражение 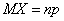определяет его ____________ ожидание

математическое

Для дискретной случайной величины выражение 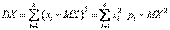называется ___________

дисперсией

Для дискретной случайной величины выражение 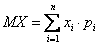называется ____________ ожиданием

математическим

Для дифференциального уравнения характеристическое уравнение имеет вид

,

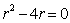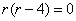
Для дифференциального уравнения 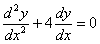характеристическое уравнение имеет вид

,

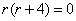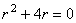
Для дифференциального уравнения 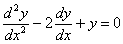характеристическое уравнение имеет вид

,

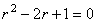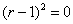
Для матрицы собственным является вектор

,

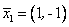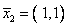
Для непрерывной случайной величины выражение 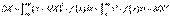называется ___________

дисперсией

Для непрерывной случайной величины выражение 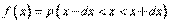называется ___________ вероятности

плотностью

Для непрерывной случайной величины выражение 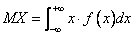называется ее ___________ ожиданием

математическим

Для построения доверительного интервала для дисперсии надо пользоваться таблицами

распределения Пирсона ( )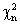

Для проверки гипотезы Н⁰, состоящей в том, что σ²¹=σ²², на уровне значимости α используется статистика F

вычисляются несмещенные оценки дисперсий s²¹и s²²и статистика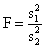

Для проверки гипотезы о виде распределения применяется статистика, имеющая распределение χ2, число степеней которого равно

m- r - 1, где m - число слагаемых, а r - число параметров распределения, замененных на эмпирические значения

Для проверки гипотезы о независимости признаков А и В произведена выборка и значения признака А сгруппированы в r интервалов, а признака В - в s интервалов. Проверка гипотезы производится с помощью статистики имеющей распределение χ2, число степеней свободы которого равно

(r-1)(s-1)

Для решения линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами (например, 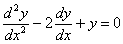) сос-тавляется соответствующее ему алгебраическое уравнение (в данном случае 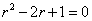), которое называется

характеристическим