Основной закон гидростатики (закон Паскаля [1]) формулируется так:
Давление, оказываемое на жидкость (или газ) в каком-либо одном месте на её границе, например, поршнем, передается без изменения во все точки жидкости (или газа).
Гидростатический парадокс — явление, при котором вес налитой в сосуд жидкости может отличаться от силы давления на дно.
Причины гидростатического парадокса кроются в разных формах сосудов. Например, если объём жидкости меньше (?) объёма прямоугольного параллелепипеда с площадью основания, равной площади дна сосуда и высотой, равной высоте сосуда, то сила давления на дно будет больше веса жидкости.
В 1648 г. парадокс продемонстрировал Б. Паскаль (рис. 2.3.1). Он вставил в закрытую бочку, наполненную водой, узкую трубку и, поднявшись на балкон второго этажа, влил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.
Рис.2.3.1
Рассмотрим распространенный случай равновесия жидкости, когда на неё действует только одна массовая сила - сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объёма жидкости. Это уравнение называется основным уравнением гидростатики.
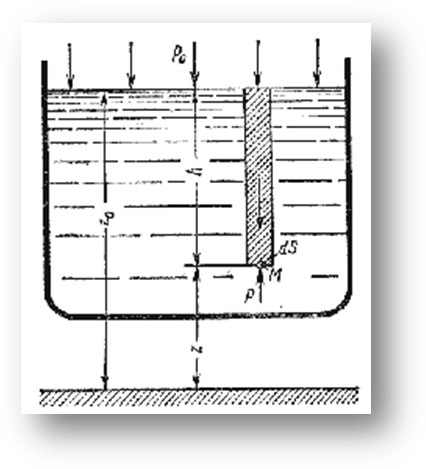
Пусть жидкость содержится в сосуде (рис. 2.8) и на ее свободную поверхность действует атмосферное давление P0 . Найдем гидростатическое давление P в произвольно взятой точке М, расположенной на глубине h. Выделим около точки М элементарную горизонтальную площадку dS и построим на ней вертикальный цилиндрический объём жидкости высотой h. Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объема, т.е. вверх.
Рис. 2.8. Схема для вывода основного уравнения
гидростатики
Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикальную ось:
PdS - P0 dS - ρ ghdS = 0
Последний член уравнения представляет собой вес жидкости, заключенный в рассматриваемом вертикальном цилиндре объемом hdS. Силы давления по боковой поверхности цилиндра в уравнение не входят, т.к. они перпендикулярны к этой поверхности и их проекции на вертикальную ось равны нулю. Сократив выражение на dS, и перегруппировав члены, найдем:
P = P0 + ρ gh = P0 + h* γ
Полученное уравнение называют основным уравнением гидростатики. По нему можно посчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления P0 на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.
Из основного уравнения гидростатики видно, что какую бы точку в объёме всего сосуда мы не взяли, на нее всегда будет действовать давление, приложенное к внешней поверхности P0. Другими словами давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем направлениям одинаково. Это положение известно под названием закона Паскаля.
Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня. В обычных условиях поверхности уровня представляют собой горизонтальные плоскости.
