Описание номограмм для расчетов при седиментационном анализе

СЕДИМЕНТАЦИОННЫЙ АНАЛИЗ

В практике физико-химического исследования суспензий очень распространённым методом является седиментационный анализ, который заключается в изучении скорости оседания - седиментации частиц, взвешенных в той или иной среде, и позволяет определить размер частиц.

Оседание частиц шарообразной формы в жидкости происходит под действием силы тяжести - веса частицы, величина которого с учётом гидростатической поправки равна:

где r - радиус частицы, D - плотность вещества частицы, d - плотность жидкости, g - ускорение силы тяжести.

Оседанию частиц противодействует сила вязкого сопротивления среды - жидкости, определяемая законом Стокса:

где r - радиус сферической частицы, η - вязкость жидкости, υ - скорость движения частицы.

Вначале, под действием постоянной силы Р частица движется равноускоренно, т.к. сила Р больше силы f. По мере увеличения скорости растет сила вязкого сопротивления среды f. К некоторому моменту времени эти силы сравниваются, вес частиц уравновешивается противоположно направленной силой f и с этого момента частица будет двигаться с постоянной скоростью (υ).Из равенства P=f

можно установить зависимость между скоростью оседания частицы и радиусом

или ,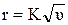

где - величина постоянная для данных условий опыта.

Это уравнение применимо при определении размеров частиц по скорости их оседания в воде для частиц диаметром от 0,1 до 100 мк; для частиц таких размеров применим закон Стокса и время нарастания скорости до постоянного значения составляет малые доли секунды и не оказывает влияния на расчёты.

Более крупные частицы, размером более 100 мк, уже значительную часть пути движутся равноускоренно, приобретая такую скорость, при которой начинается турбулизация жидкости и уравнение Стокса становится неприменимым.

Частицы размером менее 0.1 мк оседают крайне медленно и могут образовывать седиментационно - устойчивые системы, в которых оседанию частиц противодействует диффузия.

Если все частицы дисперсной системы имеют одинаковые размеры, такая система называется монодисперсной.

Оседание частиц монодисперсной системы происходит с одной и той же скоростью V, и на чашечке седиментометра будет накапливаться осадок пропорционально времени оседания τ. График кинетики накопления осадка Р=f(τ) представляет собой прямую линию (рис.1) с одной точкой перегиба В, соответствующей времени полного оседания всех частиц суспензии τ_m, т. е. времени прохождения частицами всей высоты Н столба суспензии, от её поверхности до дна чашечки.

Радиус определяется по формуле:

(1).

Оседание частиц бидисперсной системы (суспензии), имеющей две фракции частиц - мелкие и крупные, можно представить как одновременное оседание двух монодисперсных суспензий (рис.2).

Если кинетика более крупных частиц выражается прямой OВ, а более мелких - прямой ОС, то график кинетики оседания бидисперсной суспензии получается суммированием ординат этих прямых и представляет собой ломаную линию ОВС с двумя точками перегиба В и С и абсциссы этих точек τ₁ и τ₂ соответсвуют времени полного оседания крупных и мелких частиц, по которым и находятся их радиусы r₁ и r₂ по формуле 1.

По графику кинетики оседания (накопления осадка) можно предположить также и относительное содержание в % крупных Р₁ и мелких Р₂ частиц в данной бидисперсной суспензии.

Продолжив прямую В'С' до пересечения с осью ординат получим точку О₁; из чертежа видно, что ОО₁ = В'Е = СС =Р₁; О₁О₂ = СА = Р₂.

Аналогичный график можно построить и для трёхдисперсной системы (рис.3). Он будет иметь три точки перегиба, соответствующих временам τ₁, τ₂, τ₃ - окончания оседания частиц с радиусами r₁, r₂, r₃. Их относительные количества определяются также длиной отрезков, отсекаемых на оси ординат продолжениями отрезков, составляющих ломаную линию графика оседания: количество крупных частиц Р₁ - отрезок ОО₁; средних Р₂ - отрезок О₁О₂;мелких Р₃ - отрезок O₂O₃.

В случае полидисперсной системы, в которой имеются частицы различных размеров, график оседания будет иметь очень большое число изломов и будет выражаться кривой седиментации, представляющей собой предел ломаной линии с бесконечно малыми отрезками (рис.4). Такая седиментационная кривая получается опытным путём и выражает зависимость веса осевших частиц от времени: P=f(r).

В начале этой кривой имеется прямолинейный участок ОА, т.к. в начальный период времени на чашечку седиметометра оседают равномерно (но с различными скоростями) частицы всех размеров, до тех пор, пока не осядут все самые крупные частицы (точка А). С этого момента времени τ _m скорость накопления осадка уменьшается, и прямая переходит в кривую.

По времени τ_min (минимальному) рассчитывается r_max - радиус самых крупных частиц, т, к. за это время такие частицы, имея наибольшую скорость оседания, полностью осядут, в том числе и находившиеся в самом верхнем слое суспензии, пройдя путь Н - полную высоту столба суспензии над чашечкой.

Время t_min определяется по графику путём проведения касательной к седиментационной кривой, проходящей через начало координат. Касательная должна совпадать с начальным прямолинейным её участком. Из точки отрыва касательной от седиментационной кривой (точка А) опускается перпендикуляр на ось абсцисс и находится время τ_min. При временах > τ_m_ax кривая оседания полидисперсной суспензии также переходит в прямую, точка перехода К соответствует окончанию процесса оседания всех частиц суспензии. Проводя касательную к седиментационной кривой, параллельную оси абсцисс из точки К отрыва её от кривой, опускают перпендикуляр и находят на оси абсцисс время τ_m_ax, по которому рассчитывают r_min - радиус самых мелких частиц. Ордината Р_к этой касательной соответствует весу всех частиц, выпавших на чашку (100%). Вычисленные значения τ_m_ax и τ_min заносят в таблицу.

Рассмотрим произвольную точку на кривой накопления, например, Д, соответствующую времени τ₃. Все количество вещества Р = ОО₁', успевшее осесть к этому времени (отрезок Дτ₃), можно условно разбить на две фракции: 1/q₁ с частицами, радиус которых и которые за время τ₃ полностью успевают выпасть в осадок и 1/q₂ с частицами, радиус которых , которые за время τ₃ успевают лишь частично перейти в осадок.

Скорость накопления вещества в осадке ко времени τ₃, равная , определяется теми частицами, которые не успели полностью осесть, т. е. с радиусами . Эта скорость накопления для частиц данной фракции () была постоянна в течение всего опыта. Это означает, что вес частиц этой фракции, выпавших в осадок ко времени τ₃, определяется произведением постоянной скорости их накопления в осадке на время, в течение которого частицы выпали с этой скоростью, т.е.

.

Как видно из рис.4 (см. rДО₃Д₁) произведение 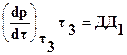, так как

, а ,

следовательно:

,

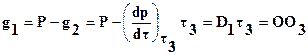т.е. касательная, проведенная к кривой накопления в точке С, отсекает на оси ординат отрезок ОО₃, который показывает вес частиц с . Отношение соответствует относительному (по весу) содержанию в суспензии частиц, размеры которых ограничены радиусами r_max и r₃, т. е. .

Аналогично этому отношение 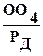показывает относительное содержание в суспензии частиц с радиусами от 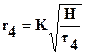до r_max, а отношение - содержание частиц с радиусом от r_max до и т.д. Результаты седиментационного анализа представляют в виде функции, отражающей распределение частиц по размерам. Обычно строят интегральную и дифференциальную кривые распределения.

Интегральная или суммарная кривая распределения Q(r) показывает зависимость от радиуса суммарного количества частиц с размерами, превышающими радиус r. Для построения интегральной кривой распределения на оси абсцисс откладывают значения радиусов в интервале r_min - r_max, а на оси ординат относительное содержание (по весу) частиц с радиусом от r_max до данного радиуса r_τ (рис. 5). Для этого к кривой накопления в отдельных точках проводят касательные до их пересечения с осью ординат (рис.4).

В таблице (см. табл. 1) отмечают значения соответствующих абсцисс:

τ, , Q

- величины относительного содержания частиц в интервале радиусов от r_min до r_τ, т.е. выраженные в % от ОР = Р_к длины участков ОО₁; ОО₂; ОО₃ и т.д.

Таблица I

Данные для построения интегральной кривой распределения

Q = f(r, т)

τ	r	Q
τ_min	r_max
τ₁	r₁
τ₂	r₂
τ₃	r₃
τ_max	r_min	100%

Важным с практической стороны свойством интегральной кривой распределения является возможность быстрого определения содержания в данной суспензии любой фракции частиц. Если нужно найти, например, количество частиц, имеющих размеры в пределах от r_n до r_m, то на интегральной кривой отмечают две точки с абсциссой r_n до r_m, разность их ординат прямо дает процентное содержание этой фракции.

Интегральная кривая обычно имеет S-образную форму, с характерной точкой перегиба, соответствующей наиболее вероятному размеру частиц, содержащихся в данной дисперсной системе.

Дифференциальная кривая распределения показывает изменение весового количества при изменении радиуса частиц на единицу вблизи данного значения радиуса . Так, например, если содержание частиц в интервале радиусов от r₁ до r₂ составляет ΔQ (рис.4), то дифференциальная функция распределения для среднего радиуса составляет

Для построения дифференциальной кривой распределения используется построенная ранее интегральная кривая, по которой и находят значения 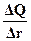для различных интервалов радиусов. Полученные данные заносят в таблицу 2.

Таблица 2

Данные для построения дифференциальной кривой распределения

r_τ	Δr	r	ΔQ
r_max	r₁- r₂		ΔQ
r₁
r₂
r₃
r_min

На графике откладывают значения в зависимости от радиуса. Кривая распределения должна быть ограничена значениями r_max и r_min (рис. 6).

Дифференциальная кривая распределения обычно имеет один максимум, соответствующий наибольшей по весу фракции и наиболее вероятному размеру частиц в данной суспензии (рис.6). Площадь, ограниченная дифференциальной кривой и осью абсцисс дает общее весовое количество частиц всех размеров (100 %), а площадь, ограниченная двумя значениями радиусов r_n и r_m - процентное содержание в суспензии частиц в интервале радиусов от r_m до r_n.

ОПИСАНИЕ НОМОГРАММ ДЛЯ расчетов ПРИ СЕДИМЕНТАЦИОННОМ АНАЛИЗЕ

(составлена проф. Н. А. Фигуровским)

Номограмма предназначена для расчёта радиусов частиц при седиментометрических определениях. В основу номограммы положено уравнение Стокса, выражающее зависимость между скоростью оседания частиц , их размерами τ и плотностью d, а также плотностью D и вязкостью η дисперсионной среды при температуре опыта.

Номограмма представляет собой семь шкал, выполненных в логарифмическом масштабе и расположенных на таком расстоянии друг от друга, что при выполнении называемых ниже последовательных операций с помощью карандаша и линейки легко определить величину радиуса оседающей по Стоксу частицы (или фракции частиц). На шкале 1а указаны разности плотностей дисперсной фазы и дисперсионной среды, на шкале 1б - вязкости, на шкале 1 -константы уравнения Стокса, увеличенные в 10⁴ раз, чтобы ответ получить в микронах. На шкале 2а - время оседания частиц данного размера, на шкале 2 даны значения корня квадратного из скорости оседания, на шкале 2б - высота оседания. Наконец, на шкале 3 приведены значения величины радиусов.

Способ определения радиуса частицы показан на номограмме. Он соответствует случаю, когда разность плотностей среды и оседающей частицы равна 1 г/см³, вязкость среды равна 0.01 пуаз. Высота Н оседания равна 10 см.

Время оседания частицы (или соответствующей фракции) равна 10 мин. - отсчёт справа по шкале 2а, (или 600 сек.) - отсчёт слева по шкале 2б. Приложив линейку к назначенным точкам шкал 1а и 1б, получаем на шкале 1 нужное значение константы Стокса для данной дисперсной системы. Затем, соединяя линейкой названные значения на шкалах 2а и 2б, получаем на шкале 2 значения корня квадратного из скорости. Наконец, приложив линейку к найденным точкам на шкале 1 и 2, соединяем их линейкой, продолжение которой до пересечения со шкалой 3 даёт искомое значение радиуса в микронах.

Часть I