Цилиндрические поверхности.

Лекция 15. Поверхности второго порядка.

Содержание лекции: Поверхности в пространстве: конические, цилиндрические, вращения. Поверхности второго порядка: сфера, конус, гиперболоиды, эллипсоид, параболоиды, цилиндрические поверхности. Канонические уравнения поверхностей.

 

В трехмерном пространстве уравнение вида определяет некоторую поверхность. Так, мы уже знаем уравнение поверхности первого порядка – плоскости .

Алгебраическое уравнение второго и выше порядков определяет в пространстве поверхности, которые так и называют поверхностями второго и более высоких порядков. Рассмотрим поверхности второго порядка и их простейшие уравнения.

Поверхности вращения

Определение 1

Поверхностью вращения называется поверхность, образованная вращением некоторой пространственной линии L (называемой образующей) вокруг заданной прямой l (называемой осью вращения), лежащей в одной плоскости с L (рисунок 1).

Очевидно, при вращении L каждая точка её описывает окружность.

Простейший случай поверхности вращения, когда кривая L вращается вокруг оси координат.

Поверхности, образованные вращением кривых второго порядка вокруг их осей симметрии, называют поверхностями вращения второго порядка.

Пусть кривая L, лежащая в плоскости у O z, вращается вокруг оси O z. Уравнения этой кривой можно записать в виде:

Пусть S - поверхность вращения, M(x, y, z) – произвольная точка этой поверхности. Проведём плоскость a O z, проходящую через точку M. Пусть O₁ точка пересечения плоскости a с O z, а точка P – с кривой L. Тогда O₁ (0,0, z), а P(0, y ₀, z), где y ₀- некоторое число.

В сечении поверхности S плоскостью a получается окружность; точки P и M лежат на этой окружности, причём радиус окружности равен |O₁M|=|O₁P|. Имеем |O₁P| = | y ₀| (так как LÎ y O z), значит, с одной стороны O₁M|= | y ₀|. В то же время

|O₁M|= = .

Следовательно, | y ₀|= , или у ₀ = ± . А так как PÎL, то её координаты удовлетворяют уравнениям кривой: , отсюда F (y ₀, z)= 0. Представив сюда y ₀ = ± , получим

F = ( ± ; z) =0,

значит координаты произвольной точки M(x, y, z), лежащей на поверхности вращения удовлетворяет уравнению F = (± ; z) = 0, значит, это уравнение есть уравнение поверхности S.

Аналогично можно вывести уравнение поверхности вращения вокруг других осей.

Отсюда мы можем вывести следующее практическое правило:

Чтобы найти уравнение поверхности вращения кривой L вокруг координатной оси, лежащей с L в одной плоскости, нужно в уравнении кривой L переменную, соответствующую оси вращения, оставить без изменения, а вторую переменную заменить на (±) корень квадратный из суммы квадратов остальных переменных.

 

Например, если L: F (x, y) = 0, LÎ x O y и вращается вокруг оси O y, то уравнение поверхности вращения F = (± ; z) = 0. Если эта кривая вращается вокруг оси O x, то уравнение поверхности запишется в виде F = (x;± ) = 0. Если L: F (x, z) = 0 вращается вокруг O z, то поверхность имеет уравнение F = (± ; z)=0 и т.д.

Например, при вращении окружности (у – a)² + z ² =1 вокруг оси О y получится шар, а при вращении вокруг оси OZ – тор (рис.)

 

Особенности: в сечении поверхности вращения плоскостями, ^ оси вращения, получаются окружности.

Рассмотрим поверхности, которые получаются при вращении кривых второго порядка.

1) - эллипс с полуосями a и b. Если вращать его вокруг оси O х, то получим поверхность с уравнением

, или .

Эта поверхность называется эллипсоидом вращения. Здесь, очевидно, ± a – отрезки, который “отсекает” эллипсоид на оси O х, ± b - отрезки на осях O у, O z, числа a, b, b в этом случае называются полуосями эллипсоида.

Аналогично, вращая эллипс вокруг O y, получим поверхность - та же структура уравнения, значит, это также эллипсоид вращения с полуосями a и b. Отличительная особенность уравнения эллипсоида вращения: сумма, 3 квадрата, две полуоси одинаковые. По этим признакам можно узнать тип поверхности.

Например: – эллипсоид вращения: эллипс вращается вокруг оси OX.

Если деформировать эллипсоид вдоль оси O z (сжать или растянуть), то уравнение приобретает вид

,

этот эллипсоид называется трехосным эллипсоидом, a, b, c - полуоси эллипсоида.

 

2) Рассмотрим гиперболу . Если вращать её вокруг оси O y, то получим поверхность с уравнением

Поверхность такого вида называется однополостным гиперболоидом вращения, a, b, a - полуоси гиперболоида. Если деформировать поверхность вдоль оси z; получим поверхность

,

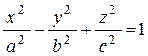которая называется просто однополостным гиперболоидом.

Отличительные особенности: 3 квадрата, один минус остальные плюсы, справа 1.

Если гиперболу вращать вокруг оси O x, получим поверхность с уравнением ,

у

х

Эта поверхность называется двуполостным гиперболоидом вращения. Если деформировать его, получим просто двуполостный гиперболоид

.,

Отличительные особенности: 3 квадрата, 2 минуса, справа 1.

 

3) Рассмотрим параболу 2 pz = у ² и будем вращать её вокруг оси O z, получим поверхность с уравнением x ² + y ² = 2 pz, или – параболоид вращения.

Если теперь деформировать эту поверхность вдоль оси О у, получим поверхность с уравнением , p, q >0, которая называется эллиптическим параболоидом

Цилиндрические поверхности.

 

Пусть L - некоторая линия в пространстве, а l – прямая, не лежащая с L в одной плоскости.

Определение 8.2.

Цилиндрической поверхностью называется множество точек пространства, являющееся объединением всех прямых, параллельных заданной прямой l и проходящих через точки кривой L. Линия L называется направляющей, а прямые, параллельные прямой l - образующими цилиндра.

Рассмотрим цилиндрические поверхности с образующими, параллельными осям координат, а направляющими, лежащими в координатных плоскостях.

Пусть L: - кривая в пространстве (очевидно, она лежит в плоскости x O y), а l = O z.

Рассмотрим цилиндрическую поверхность. Пусть M(x, y, z) – произвольная точка этой поверхности. Тогда проекция M₁ (x, y, 0) этой точки на плоскость x O y лежит на направляющей L. Значит, её координаты x и y удовлетворяют уравнению L:

F (x, y) = 0.

Наоборот, если точка N(x ₁, y ₁, z ₁) не принадлежит цилиндрической поверхности, то F (x ₁, y ₁) ¹ 0 (N ÏL), то есть уравнению F (x, y) = 0, удовлетворяют координаты точек цилиндрической поверхности и только они, следовательно, F (x, y) = 0 есть уравнение цилиндрической поверхности с направляющей и образующей, параллельной O z.

Аналогично можно показать, что уравнение F(x, z)=0 определяет цилиндрическую поверхность с образующей, параллельной O y и направляющей

Уравнение F (y, z)=0 определяет цилиндрическую поверхность с направляющей и образующей, параллельной оси O x.

Цилиндрическая поверхность, у которой направляющая есть кривая 2-го порядка, называется цилиндрической поверхностью 2-го порядка.

Например, поверхность (или ) называется параболическим цилиндром.

 

Поверхность с уравнением или - эллиптический цилиндр:

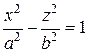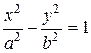Уравнения и определяют гиперболический цилиндр:

 

 

 

Конические поверхности.

Пусть L - некоторая кривая и точка AÏL и не лежит с L в одной плоскости. Рассмотрим множество точек лежащих на прямых AM, где M – произвольная точка кривой L, это множество точек называется конусом с вершиной в точке A и направляющей L.

Определение 3.

Поверхность, образованная прямыми линиями, проходящими через заданную точку А и точки кривой L, называется конической поверхностью или конусом. Точка А называется в ершиной конуса, кривая L – направляющей, прямые АМ, где МÎL, называются образующими конуса.

Если направляющая конуса есть кривая второго порядка, не лежащая в одной плоскости с вершиной, то конус называется конусом второго порядка.

 

Например, если направляющей конуса является эллипс , а вершина – начало координат, то уравнение конуса имеет вид , это конус 2-го порядка.