В реальных электрических схемах цепей четырехполюсник включается в нагруженном режиме со стороны выходных и входных зажимов произвольными нагрузками Z Н2 и Z Н1 соответственно(рис. 5.7, а, б).
 |
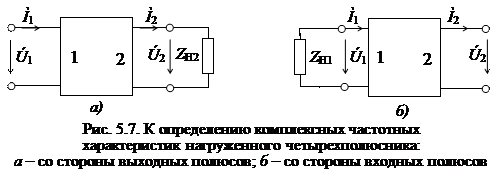В качестве комплексных частотных характеристик чаще всего рассматривают входное Z 11(j ω) и выходное Z 22(j ω) сопротивления и коэффициенты передачи по напряжению K U21(j ω) и току K I21(j ω). Эти параметры можно выразить через первичные параметры. Для примера определим комплексные частотные характеристики в системе A-параметров.
Ток и напряжение на выходных зажимах связаны соотношением
Ì 2 = Ú 2/ Z Н2,
используя которое основные уравнения четырехполюсника (5.7) могут быть преобразованы к виду:
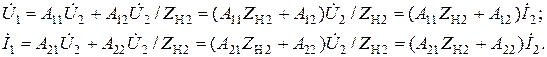(5.17)
Из уравнений (5.17) следует, что
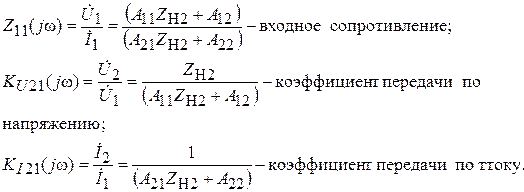(5.18)
Полученные формулы (5.18) показывают, что частотные характеристики Z 11(j ω), K U21(j ω), K I21(j ω) четырехполюсника определяются не только первичными параметрами, но и сопротивлением нагрузки.
Рассмотрим случай так называемого обратного включения (рис. 5.7, б), когда сопротивление нагрузки
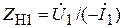(5.19)
подключено к входным полюсам.
При изменении направления передачи в выражениях (5.18) параметры A 11 и A 22 и номера полюсов меняются местами:
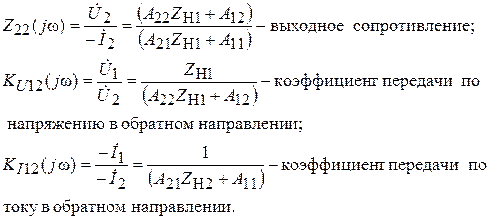(5.20)
Как видно по выражениям (5.20) частотные характеристики четырехполюсника в обратном направлении зависят и от первичных параметров и от сопротивления нагрузки на входе Z Н1.
ХАРАКТЕРИСТИЧЕСКИЕ ПАРАМЕТРЫ
ЧЕТЫРЕХПОЛЮСНИКА
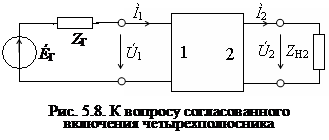
Согласованное включение четырехполюсника. При передаче сигналов по цепи может участвовать большое число каскадно-соединенных четырехполюсников. На практике используется такое включение, которое получило название согласованного. Если рассматривать четырехполюсник, включенный по схеме рис. 5.8, то это означает, что должны выполняться два условия согласования по входным и выходным полюсам:
Z 11 = Z Г и Z 22 = Z Н2, т.е. входное сопротивление четырехполюсника должно быть согласовано с сопротивлением генератора, а выходное – с сопротивлением нагрузки.
Режим согласованного включения является наиболее благоприятным при передаче сигналов, поскольку при этом отсутствует отражения электрической энергии на стыках «генератор – четырехполюсник» и «четырехполюсник – нагрузка» и искажение сигнала.
Характеристические сопротивления четырехполюсника. Для любого четырехполюсника можно подобрать пару сопротивлений Z 01 и Z 02, при подключении которых четырехполюсник приобретает «характерные свойства», поэтому их называют характеристическими:
а) если сопротивление нагрузки взять равным характеристическому Z Н2 = Z 02, то входное сопротивление станет равным другому характеристическому Z 11 = Z 01;
б) если сопротивление генератора взять равным характеристическому Z Г = Z 01, то выходное сопротивление четырехполюсника станет равным другому характеристическому Z 22 = Z 02.
Если использовать эти свойства в выражениях Z 11 (5.18) и Z 22 (5.20), то можно определить значения характеристических сопротивлений
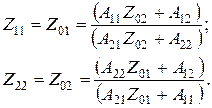(5.21)
Совместное решение этих уравнений относительно Z 01 и Z 02 дает выражения характеристических сопротивлениях через A-параметры:
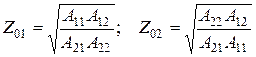. (5.22)
Если четырехполюсник симметричный, т.е. A 11 = A 22, то характеристические входное и выходное сопротивления одинаковы:
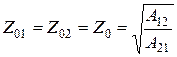. (5.23)
Характеристическая постоянная передачи четырехполюсника. При согласованном включении четырехполюсника на входе и выходе потери (рассеяние) электрической энергии будет происходить только в четырехполюснике (например, она будет превращаться в тепловую энергию на резистивных элементах схемы).
Чтобы учесть эти потери, вводят меру передачи энергии - характеристическую постоянную передачи четырехполюсника, определяемую через отношение произведения комплексных напряжения и тока на входе к произведению комплексных напряжения и тока на выходе четырехполюсника, взятое в логарифмическом масштабе
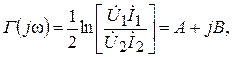(5.24)
причем все токи и напряжения измеряются или вычисляются в режиме согласованного включения четырехполюсника, т.е. Z Г = Z 01 и Z Н = Z 02.
Так как Ú 1 = Ì 1 Z 11 = Ì 1 Z 01 и Ú 2 = Ì 2 Z 22 = Ì 2 Z 02, характеристическую постоянную передачи можно представить в другой форме записи
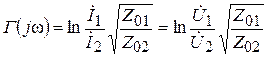. (5.25)
Если четырехполюсник симметричный, то из (5.23) следует, что выражение (5.25) примет вид
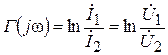. (5.26)
Для определения вещественной A и мнимой B составляющих выражения (5.25) представим напряжения и токи в показательной форме:
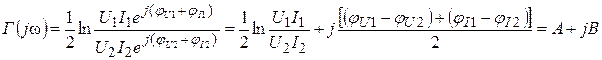. (5.27)
Величина
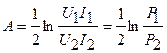, (5.28)
где P 1 и P 2 – полные мощности на входе и выходе четырехполюсника при согласованном его включении, называется характеристическим ослаблением четырехполюсника. Она показывает в логарифмическом масштабе, на сколько уменьшилась мощность на выходе четырехполюсника по сравнению с мощностью на его входе при передаче энергии через четырехполюсник в согласованном режиме.
Для симметричного четырехполюсника из (5.26) получаем
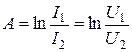. (5.29)
Единица измерения отношений величин в масштабе натуральных логарифмов называется непером (сокращенно Нп). На практике принято вычислять и измерять ослабление в других единицах – Беллах (сокращенно Б). Ослаблению в 1 Б соответствует уменьшение мощности в 10 раз, ослаблению 2 Б – в 100 раз и т.д. Вместо формулы (5.28) в этом случае используют формулу
.
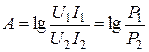Бел достаточно крупная единица измерения. Вместо нее обычно применяют в 10 раз меньшую единицу – децибел (сокращенно дБ). Поскольку 1 Б = 10 дБ, то
.
Для симметричных четырехполюсников вместо (5.29) удобно пользоваться формулой
.
Второе слагаемое в формуле (5.27)
учитывает изменение начальных фаз напряжений и токов при передаче энергии через согласованно включенный четырехполюсник и носит название характеристической фазы или фазовой постоянной четырехполюсника.
Преобразование (5.26) для симметричного четырехполюсника приводит к характеристической фазовой постоянной, равной разности фаз входного и выходного напряжений или токов:
B = φU1 – φU2 = φI1 – φI2.
Измеряется фазовая постоянная в радианах (сокращенно рад) или градусах (сокращенно град).
Величины Z 01, Z 02 и Г образуют систему характеристических параметров четырехполюсника. Она полностью описывает пассивный четырехполюсник.
