ХІІІ обласна математична олімпіада
Імені акад. М.П. Кравчука
Рік
Класи (2015-2016 н.р.) Заочний тур
Розв’язання задач заочного туру надіслати до 15 серпня 2016 року в електронному варіанті
(e-mail: btv_1963@ukr.net, моб. тел. 0965653335).
Вимоги до оформлення роботи заочного туру олімпіади:
1)відповідь до кожної задачі обґрунтуйте; подайте у розв’язаннях детальні пояснення, виконавши при потребі малюнки, креслення, схеми і т. ін.;
2) розв’язання задач набирати українською моваю, орієнтація – книжкова; поля: верхній, нижній, лівий, правий – 20 мм; шрифт: гарнітура – Times New Roman, кегль – 14, міжрядковий інтервал – 1,5; стиль – Normal (звичайний);
3) математичні формули набирати, використовуючи редактор формул;
4) оформити презентацію в Power Point, в якій подати розв’язання циклу деяких взаємопов’язаних задач (дотримуватись загальних вимог до укладання презентації).
Для участі в Очному турі олімпіади будуть допущені учасники Заочного туру, які правильно розв’язали і грамотно оформили найбільшу кількість задач із запропонованої добірки. Задачі не повинні бути одноманітними. При оцінюванні робіт учасників олімпіади члени журі звертатимуть увагу на різні аспекти: підхід до відбору задач, повнота обгрунтувань (наявніть опису процесу пошуку способу розв’язування, вибору методу розв’язування, детальне пояснення кожного кроку розв’язування в логічній послідовності), загальна мовна грамотність, рівень сформованості і розвитку писемного математичного мовлення і т. ін.
УВАГА!
Запропонований матеріал (добірки задач) допоможе школярам поглибити свої знання з теми "ЗАМОЩЕННЯ КЛІТЧАСТОЇ ДОШКИ ФІГУРАМИ ПОЛІМІНО". Наполеглива робота над розв’язуванням задач сприятиме формуванню і розвитку в них дослідницьких умінь та навиків, необхідних для ефективної підготовки до інтелектуальних змагань і конкурсів різних рівнів.
ЗАМОЩЕННЯ КЛІТЧАСТОЇ ДОШКИ ФІГУРАМИ ПОЛІМІНО
ТЕОРЕТИЧНІ ВІДОМОСТІ
Будемо говорити, що фігура  покрита фігурами
покрита фігурами  ,
,  ,
,  , …,
, …,  , якщо
, якщо 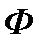 міститься в об’єднанні цих фігур, тобто будь-яка точка фігури
міститься в об’єднанні цих фігур, тобто будь-яка точка фігури  належить хоча б одній з фігур
належить хоча б одній з фігур  ,
,  ,
,  , …,
, …,  . Якщо ж фігури
. Якщо ж фігури  ,
,  ,
,  , …,
, …,  не перетинаються (не мають внутрішніх точок) і їх об’єднання співпадає з
не перетинаються (не мають внутрішніх точок) і їх об’єднання співпадає з  , то будемо говорити, що
, то будемо говорити, що 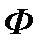 замощена фігурами
замощена фігурами  ,
, 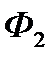 ,
,  , …,
, …,  .
.
Нагадуємо, що при розв’язуванні задач на замощення клітчастих дошок фігурками поліміно. Фігурки можна повертати, але не дозволяється їх перевертати.
ДОМІНО
Для учнів 6-7 класів
1. Яку мінімальну кількість мономіно необхідно, щоб "витіснити" на квадратній клітчастій дошці розміром  доміно?
доміно?
2.
2.1.Чи можна замостити фігурками доміно
а) клітчасту дошку розміром  ;
;
б) клітчасту дошку розміром  з вирізаною кутовою клітинкою;
з вирізаною кутовою клітинкою;
в) клітчасту дошку розміром  з вирізаними лівою верхньою і правою верхньою кутовими клітинками;
з вирізаними лівою верхньою і правою верхньою кутовими клітинками;
г) клітчасту дошку розміром  з вирізаними лівою нижньою і правою верхньою кутовими клітинками? Або: Чи можна клітчасту дошку розміром 8×8, з якої вирізана пара протилежних кутових клітинок, замостити клітинковими фігурками доміно, кожне з яких покриває рівно дві клітинки клітчастої дошки?
з вирізаними лівою нижньою і правою верхньою кутовими клітинками? Або: Чи можна клітчасту дошку розміром 8×8, з якої вирізана пара протилежних кутових клітинок, замостити клітинковими фігурками доміно, кожне з яких покриває рівно дві клітинки клітчастої дошки?
Або: Чи можна клітчасту дошку розміром  замостити фігурками доміно так, щоб вільними залишилися лише дві протилежні кутові клітинки?
замостити фігурками доміно так, щоб вільними залишилися лише дві протилежні кутові клітинки?
2.2. Розв’язавши задачі а-г п. 2.1., у тих випадках, коли замощення існує, з’ясуйте питання про парність числа, яким визначається кількість горизонтально розміщених кісточок доміно і кількість вертикально розміщених кісточок доміно.
3. Клітчастий прямокутник розміром  замостили клітинковими фігурками розміром
замостили клітинковими фігурками розміром  – фігурками доміно. Доведіть, що на цей шар з фігур доміно можна накласти другий шар так, що жодна фігура доміно другого шару не співпадає з фігурою першого шару.
– фігурками доміно. Доведіть, що на цей шар з фігур доміно можна накласти другий шар так, що жодна фігура доміно другого шару не співпадає з фігурою першого шару.
4. Прямокутник покрито у два шари картками  (над кожною клітинкою лежить рівно дві картки). Доведіть, що картки можна розбити на дві множини, що не перетинаються, кожна з яких покриває весь прямокутник.
(над кожною клітинкою лежить рівно дві картки). Доведіть, що картки можна розбити на дві множини, що не перетинаються, кожна з яких покриває весь прямокутник.
5. а) Чи можна прямокутник розміром  замостити костями доміно
замостити костями доміно  так, щоб не було "шва", тобто прямої, яка не розрізає костей доміно?
так, щоб не було "шва", тобто прямої, яка не розрізає костей доміно?
б) Чи можна прямокутник розміром  замостити костями доміно
замостити костями доміно  так, щоб не було "шва", тобто прямої, яка не розрізає костей доміно?
так, щоб не було "шва", тобто прямої, яка не розрізає костей доміно?
в) Чи можна квадрат розміром  замостити костями доміно
замостити костями доміно  так, щоб не було "шва", тобто прямої, яка не розрізає костей доміно?
так, щоб не було "шва", тобто прямої, яка не розрізає костей доміно?
г) Доведіть, що будь-який прямокутник  , де
, де 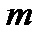 і
і  більші за 6 і
більші за 6 і  парне, можна замостити костями доміно так, щоб не було "шва".
парне, можна замостити костями доміно так, щоб не було "шва".
д) Доведіть, що прямокутник  можна замостити костями доміно
можна замостити костями доміно  так, щоб не було "шва".
так, щоб не було "шва".
6. а) З квадратної клітчастої дошки розміром 6´6 вирізали квадрат з чотирьох клітинок. Доведіть, що ту частину дошки, що залишилася, можна замостити фігурками доміно (прямоугольники 2´1) так, що число горизонтальных доміно дорівнює числу вертикальних.
б) Чи правильне таке ж твердження для клітчастої дошки розміром 8´8 с вирізаним квадратом з чотирьох клітинок?
ТРИМІНО
1. Чи можна замостити прямокутну клітчасту дошку розміром  триклітинковими кутиками – фігурками прямокутного триміно так, щоб жодні два триміно не утворювали прямокутник розміром
триклітинковими кутиками – фігурками прямокутного триміно так, щоб жодні два триміно не утворювали прямокутник розміром  ?
?
2. Чи можна замостити прямокутну клітчасту дошку розміром  триклітинковими кутиками – фігурками прямокутного триміно так, щоб не було прямих "швів"?
триклітинковими кутиками – фігурками прямокутного триміно так, щоб не було прямих "швів"?
3. Чи можна замостити прямокутну клітчасту дошку розміром  триклітинковими кутиками – фігурками прямокутного триміно так, щоб не було прямих "швів"?
триклітинковими кутиками – фігурками прямокутного триміно так, щоб не було прямих "швів"?
4. Чи можна замостити прямокутну клітчасту дошку розміром  триклітинковими кутиками – фігурками прямокутного триміно так, щоб не було прямих "швів"
триклітинковими кутиками – фігурками прямокутного триміно так, щоб не було прямих "швів"
5. Чи можна замостити квадратну клітчасту дошку розміром  триклітинковими кутиками – фігурками прямокутного триміно так, щоб жодні два триміно не утворювали прямокутник розміром
триклітинковими кутиками – фігурками прямокутного триміно так, щоб жодні два триміно не утворювали прямокутник розміром  ?
?
6. Чи можна замостити квадратну клітчасту дошку розміром 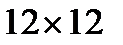 триклітинковими кутиками – фігурками прямокутного триміно так, щоб жодні два триміно не утворювали прямокутник розміром
триклітинковими кутиками – фігурками прямокутного триміно так, щоб жодні два триміно не утворювали прямокутник розміром  ?
?
7. Чи можна замостити прямокутну клітчасту дошку розміром 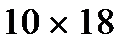 триклітинковими кутиками – фігурками прямокутного триміно так, щоб жодні два триміно не утворювали прямокутник розміром
триклітинковими кутиками – фігурками прямокутного триміно так, щоб жодні два триміно не утворювали прямокутник розміром  ?
?
8. Яке найбільше число триклітинкових кутиків можна вирізати з клітчастого прямокутника розміром  ? Відповідь обгрунтуйте. Подайте детальні пояснення.
? Відповідь обгрунтуйте. Подайте детальні пояснення.
9. Яке найбільше число триклітинкових кутиків можна вирізати з клітчастого квадрата розміром  ? Відповідь обгрунтуйте. Подайте детальні пояснення.
? Відповідь обгрунтуйте. Подайте детальні пояснення.
10. Чи можна клітчастий квадрат розміром  замостити триклітинковими кутиками (L-триміно)?
замостити триклітинковими кутиками (L-триміно)?
11. Чи можна зображену на малюнку фігуру з 60 клітинок замостити двадцятьма прямими триміно (розмір клітинки триміно співпадає з розміром клітинки фігури)?

12. а) З квадратної клітчастої дошки розміром  вирізали одну клітинку. Одержану фігуру замостили триклітинковими фігурами – прямими триміно (I-триміно). Яку клітинку вирізали з дошки?
вирізали одну клітинку. Одержану фігуру замостили триклітинковими фігурами – прямими триміно (I-триміно). Яку клітинку вирізали з дошки?
б) З 16 плиток розміром  та однієї плитки розміром
та однієї плитки розміром  склали квадрат зі стороною 7. Доведіть, що плитка
склали квадрат зі стороною 7. Доведіть, що плитка  або лежить у центрі квадрата, або прилягає до його межі.
або лежить у центрі квадрата, або прилягає до його межі.
Або:
У квадраті  розміщено 16 плиток розміром
розміщено 16 плиток розміром  та одна плитка
та одна плитка  . Доведіть, що плитка
. Доведіть, що плитка  або лежить у центрі квадрата, або прилягає до його межі.
або лежить у центрі квадрата, або прилягає до його межі.
в) Чи можна замостити квадратну клітчасту дошку розміром  з вирізаною клітинкою триклітинковими прямокутниками – прямими триміно?
з вирізаною клітинкою триклітинковими прямокутниками – прямими триміно?
Те ж саме: Чи можна з клітчастої квадратної дошки розміром  вирізати одну клітинку так, щоб ту частину, яка залишилася, можна було замостити плитками розміром
вирізати одну клітинку так, щоб ту частину, яка залишилася, можна було замостити плитками розміром  (фігурками І-триміно)?
(фігурками І-триміно)?
Або: Чи можна замостити квадратну клітчасту дошку розміром  триклітинковими прямокутниками – прямим триміно і одним мономіно? Відповідь обгрунтуйте. Подайте детальні пояснення.
триклітинковими прямокутниками – прямим триміно і одним мономіно? Відповідь обгрунтуйте. Подайте детальні пояснення.
13. а) Чи можна замостити квадратну клітчасту дошку розміром  з вирізаною клітинкою триклітинковими фігурками – триклітинковими кутиками? Відповідь обгрунтуйте. Подайте детальні пояснення.
з вирізаною клітинкою триклітинковими фігурками – триклітинковими кутиками? Відповідь обгрунтуйте. Подайте детальні пояснення.
б) З квадратної клітчастої дошки розміром  довільним чином вирізали одну клітинку. Чи можна фігуру, що утворилася замостити триклітинковими кутиками?
довільним чином вирізали одну клітинку. Чи можна фігуру, що утворилася замостити триклітинковими кутиками?
в) З квадратної клітчастої дошки розміром  довільним чином вирізали одну клітинку. Чи можна фігуру, що утворилася замостити триклітинковими кутиками?
довільним чином вирізали одну клітинку. Чи можна фігуру, що утворилася замостити триклітинковими кутиками?
14. Яку мінімальну кількість мономіно необхідно для того, щоб "витіснити" на квадратній клітчастій дошці розміром  :
:
а) прямокутне триміно – триклітинковий кутик (L-триміно);
б) пряме триміно (I-триміно)?
ТЕТРАМІНО
1. Чи можна замостити чотириклітинковими кутиками – фігурками прямокутного тетраміно (L-тетраміно) прямокутну клітчасту дошку розміром
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  ;
;
і т. д. так, щоб не було прямих "швів"?
2. У клітчастому квадраті розміром  зафарбуйте найменшу кількість клітинок так, щоб у фігурі, яка залишилася, не можна було помістити чотириклітинкову фігурку виду L-тетраміно.
зафарбуйте найменшу кількість клітинок так, щоб у фігурі, яка залишилася, не можна було помістити чотириклітинкову фігурку виду L-тетраміно.
3. Яку мінімальну кількість мономіно необхідно для того, щоб "витіснити" на квадратній клітчастій дошці розміром  :
:
а) L-тетраміно;
б) T-тетраміно;
в) О-тетраміно;
г) Z-тетраміно;
д) І-тетраміно?
4. Чи можна замостити двадцятиклітинковий прямокутник чотириклітинковими фігурками – фігурками І, L, T, Z, O-тетраміно? Тетраміно кожного виду необхідно використати принаймні один раз. Відповідь обгрунтуйте. Подайте детальні пояснення.Зверніть увагу на прямокутники всіх можливих розмірів.
5. З’ясуйте, чи можна замостити 24, 28, 32, 36, 40-клітинкові прямокутники чотириклітинковими фігурками – фігурками І, L, T, Z, O-тетраміно. Відповіді обгрунтуйте. Подайте детальні пояснення. Зверніть увагу на прямокутники всіх можливих розмірів.
6. Чи можна замостити фігурками I-тетраміно
а) квадратну клітчасту дошку розміром 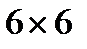 ;
;
б) прямокутну клітчасту дошку розміром  ?
?
7. Чи можна замостити квадратну клітчасту дошку розміром  фігурками
фігурками
а) I-тетраміно;
б) L-тетраміно;
в) Т-тетраміно?
8. Чи можна замостити квадратну клітчасту дошку розміром  чотириклітинковими фігурками – L-тетраміно та одним O-тетраміно? Відповідь обгрунтуйте. Подайте детальні пояснення.
чотириклітинковими фігурками – L-тетраміно та одним O-тетраміно? Відповідь обгрунтуйте. Подайте детальні пояснення.
9. Чи можна замостити квадратну клітчасту дошку розміром  чотириклітинковими фігурками: одним O-тетраміно, а решта – іншими тетраміно, серед яких декілька (або всі) – прямі (I-тетраміно), інші – косі (Z-тетраміно)? Відповідь обгрунтуйте. Подайте детальні пояснення.
чотириклітинковими фігурками: одним O-тетраміно, а решта – іншими тетраміно, серед яких декілька (або всі) – прямі (I-тетраміно), інші – косі (Z-тетраміно)? Відповідь обгрунтуйте. Подайте детальні пояснення.
10. Чи можна замостити прямокутну клітчасту дошку розміром  фігурками Т-тетраміно?
фігурками Т-тетраміно?
11. а) Чи можна замостити квадратну клітчасту дошку розміром  фігурками Т-тетраміно?
фігурками Т-тетраміно?
б) Чи можна клітчастий квадрат розміром  замостити фігурками T-тетраміно?
замостити фігурками T-тетраміно?
12. Чи можна замостити фігурками L-тетраміно прямокутну клітчасту дошку розміром
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д) 
без прямих "швів"? Відповіді обгрунтуйте. Подайте детальні пояснення.
ТРИМІНО І ТЕТРАМІНО
1. Чи можна замостити прямокутну клітчасту дошку розміром  триклітинковими кутиками (прямокутними триміно) і квадратами розміром
триклітинковими кутиками (прямокутними триміно) і квадратами розміром  (O-тетраміно)? Якщо можна, то вкажіть скільки всього фігур використали для замощування. Якщо ж не можна, топоясніть чому. Відповіді обгрунтуйте. Подайте детальні пояснення.
(O-тетраміно)? Якщо можна, то вкажіть скільки всього фігур використали для замощування. Якщо ж не можна, топоясніть чому. Відповіді обгрунтуйте. Подайте детальні пояснення.
ПЕНТАМІНО
Поліміно, які покривають п’ять клітинок клітчастої дошки, називають пентаміно.
1. З’ясуйте, скільки є різних видів фігур пентаміно. Зобразіть їх.
Є 12 видів пентаміно, які можна позначити прописними латинськими буквами T, U,V, W, X, Y, Z, F, I, L, P, N.
2. З’ясуйте, чи можна замостити клітинкові прямокутники п’ятиклітинковими фігурками – фігурами T, U, V, W, X, Y, Z, F, I, L, P, N-пентаміно.Пентаміно кожного виду необхідно використати принаймні один раз. Відповіді обгрунтуйте. Подайте детальні пояснення.Зверніть увагу на прямокутники всіх можливих розмірів.
3. Зі смужок розміром  складено прямокутник. Доведіть, що одна з його сторін ділиться на 5.
складено прямокутник. Доведіть, що одна з його сторін ділиться на 5.
4. Чи можна замостити шістдесятиклітинковий прямокутник п’ятиклітинковими фігурами – фігурами T, U, V, W, X, Y, Z, F, I, L, P, N-пентаміно? Пентаміно кожного виду можна використовувати рівно один раз.
5. Яке найбільше число п’ятиклітинкових смужок (I-пентаміно) можна вирізати з клітчастого квадрата розміром  ? Відповідь обгрунтуйте. Подайте детальні пояснення.
? Відповідь обгрунтуйте. Подайте детальні пояснення.
6. Яку мінімальну кількість мономіно необхідно для того, щоб після цього було б неможливо розмістити на квадратній клітчастій дошці розміром  хоча б одне:
хоча б одне:
а) I-пентаміно;
б) Y-пентаміно;
в) V-пентаміно;
г) T-пентаміно;
д) W-пентаміно;
е) X-пентаміно;
є) Y-пентаміно;
ж) F-пентаміно;
з) Z-пентаміно;
и) U-пентаміно;
і) L-пентаміно;
ї) P-пентаміно?
Примітка. "Розв’язати задачу" тут означає, по-перше, навести приклад розміщення на клітчастій дошці декількох моно міно, які "витісняють" задане пентаміно, і, по-друге, довести (тим або іншим комбінаторним міркуванням або ж просто баченням очевидності), що меншого числа мономіно для цієї мети не вистачить.
7. Яку мінімальну кількість мономіно необхідно для того, щоб "витіснити" на нескінченній клітчастій дошці одночасно усі:
а) I-пентаміно;
б) Y-пентаміно;
в) V-пентаміно;
г) T-пентаміно;
д) W-пентаміно;
е) X-пентаміно;
є) Y-пентаміно;
ж) F-пентаміно;
з) Z-пентаміно;
и) U-пентаміно;
і) L-пентаміно;
ї) P-пентаміно?
8. Від квадратної клітчастої дошки розміром  відрізали чотири кутових квадрати
відрізали чотири кутових квадрати  . Чи можна фігуру, що утворилася замостити п’ятиклітинковими фігурами трьох видів: T, V, X-пентаміно?
. Чи можна фігуру, що утворилася замостити п’ятиклітинковими фігурами трьох видів: T, V, X-пентаміно?
ПЕНТАМІНО І ДОМІНО
1. Чи можна квадратну клітчасту дошку розміром 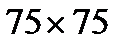 замостити клітинковими фігурками, кожна з яких є або двоклітинковим прямокутником (прямокутником
замостити клітинковими фігурками, кожна з яких є або двоклітинковим прямокутником (прямокутником 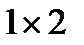 ) або фігуркою X-пентаміно?
) або фігуркою X-пентаміно?
ГРА "МОРСЬКИЙ БІЙ"
1. Гра "Морський бій" відбувається у квадраті  клітинок. Яке найменше число "пострілів" необхідно зробити, щоб гарантовано "поранити" чотирьохпалубний корабель, якщо відомо, що він має вигляд І-тетраміно? Відповідь обґрунтуйте.
клітинок. Яке найменше число "пострілів" необхідно зробити, щоб гарантовано "поранити" чотирьохпалубний корабель, якщо відомо, що він має вигляд І-тетраміно? Відповідь обґрунтуйте.
2. За яку найменшу кількість "пострілів" можна гарантовано влучити у чотирьохпалубний корабель у грі "морський бій" на дошці розміром  ? Відповідь обґрунтуйте.
? Відповідь обґрунтуйте.
3.На квадратному клітчастому полі розміром  розміщена ескадра з 10 кораблів. Кораблі – це прямокутники
розміщена ескадра з 10 кораблів. Кораблі – це прямокутники  , зі сторонами по лініях сітки, які не мають спільних точок. Доведіть, що можна зробити 32 "постріли" так, щоб гарантовано поранити корабель.
, зі сторонами по лініях сітки, які не мають спільних точок. Доведіть, що можна зробити 32 "постріли" так, щоб гарантовано поранити корабель.
4. Яке найменше число "пострілів" необхідно зробити, щоб гарантовано "поранити" пятипалубний корабель на дошці розміром 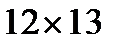 , якщо відомо, що він має вигляд І-пентаміно? Відповідь обґрунтуйте.
, якщо відомо, що він має вигляд І-пентаміно? Відповідь обґрунтуйте.
НАБІР "ЮНИЙ ПАРКЕТНИК"
1. Дно коробки розміром  вимощене плитками розміром
вимощене плитками розміром 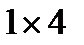 та
та  . Одну з цих плиток розміром
. Одну з цих плиток розміром  загубили, але в запасі є плитка розміром
загубили, але в запасі є плитка розміром  . Чи можна наявними плитками знову вимостити дно коробки?
. Чи можна наявними плитками знову вимостити дно коробки?
2. Дно прямокутної коробки викладено плитками розміром 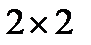 і
і 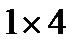 . Плитки висипали з коробки і загубили одну плитку розміром
. Плитки висипали з коробки і загубили одну плитку розміром 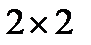 . Замість неї дістали плитку
. Замість неї дістали плитку 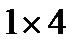 . Доведіть, що викласти дно коробки плитками тепер не вдасться.
. Доведіть, що викласти дно коробки плитками тепер не вдасться.
3. Андрійкові подарували набір "Юний паркетник", що складається з дванадцяти плиток виду I-триміно та L-триміно. Миколка замінив одну з них на триклітинковий кутик – L-триміно.Чи зможе Андрійко скласти квадрат розміром 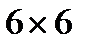 ?
?
Для учнів 6-9 класів
ГЕКСАМІНО
1. З’ясуйте, скільки є різних видів фігур пентаміно. Зобразіть їх.
2. Чи можна замостити 210-клітинковий прямокутник шестиклітинковими фігурками – фігурками гексаміно? (Або: Чи можна ли скласти з фігурок гексаміно210-клітинковий прямокутник)? Гексаміно кожного виду можна використовувати рівно один раз.
3. Чи можна замостити прямокутну клітчасту дошку розміром  шестиклітинковими прямокутниками – прямим гексаміно (І-гексаміно)?
шестиклітинковими прямокутниками – прямим гексаміно (І-гексаміно)?
4. Зі смужок розміром 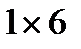 складено прямокутник. Доведіть, що одна з його сторін ділиться на 6.
складено прямокутник. Доведіть, що одна з його сторін ділиться на 6.
5. Які з фігурок гексаміно не можуть бути розгортками куба (гексаедра)?
МОДИФІКАЦІЇ ТА УЗАГАЛЬНЕННЯ
1. Доведіть, що будь-який прямокутник  , де
, де 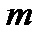 і
і  більші за 6 і
більші за 6 і  парне, можна замостити костями доміно так, щоб не було "шва".
парне, можна замостити костями доміно так, щоб не було "шва".
2. З квадратної клітчастої дошки  вирізали одну кутову клітинку. Чи можна одержану фігуру замостити фігурами доміно так, щоб було порівну горизонтально і вертикально розміщених доміно?
вирізали одну кутову клітинку. Чи можна одержану фігуру замостити фігурами доміно так, щоб було порівну горизонтально і вертикально розміщених доміно?
3. Чи можна знайти мінімальне число мономіно для того, щоб "витіснити" на клітчастій дошці розміром  одночасно:
одночасно:
а) усі 12 пентаміно;
б) 11 із 12 пентаміно;
в) кожного з дванадцяти видів пентаміно зокрема (I-пентаміно; Y-пентаміно; V-пентаміно; T-пентаміно; W-пентаміно; X-пентаміно; Y-пентаміно; F-пентаміно; Z-пентаміно; U-пентаміно; L-пентаміно; P-пентаміно);
г) якихось два види пентаміно;
д) якихось три види пентаміно;
е) якихось чотири види пентаміно і т.д.
4. Чи можна знайти мінімальне число мономіно для того, щоб "витіснити" на нескінченній клітчастій дошці одночасно:
а) усі 12 пентаміно;
б) 11 із 12 пентаміно;
в) кожного з дванадцяти пентаміно окремо;
г) якихось два види пентаміно;
д) якихось три види пентаміно;
е) якихось чотири види пентаміно і т.д.
5. З прямокутної клітчастої дошки зі стороною а)  ; б)
; б)  вирізано одну клітинку. Доведіть, що ту частину дошки, що залишилася, можна замостити фігурками триміно – триклітинковими кутиками.
вирізано одну клітинку. Доведіть, що ту частину дошки, що залишилася, можна замостити фігурками триміно – триклітинковими кутиками.
6. а) Знайдіть усі такі натуральні числа 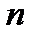 , що квадратну клітчасту дошку
, що квадратну клітчасту дошку  можна замостити прямокутними триміно.
можна замостити прямокутними триміно.
б) Знайдіть усі такі натуральні числа 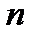 , що тороїдальну дошку, одержану з квадратної клітчастої дошки
, що тороїдальну дошку, одержану з квадратної клітчастої дошки  , можна замостити прямокутними триміно.
, можна замостити прямокутними триміно.
7. Доведіть, що число способів розрізати прямокутник  на триклітинкові кутики не перевищує числа способів розрізати прямокутник
на триклітинкові кутики не перевищує числа способів розрізати прямокутник  на такі ж кутики так, щоб жодні два такі триміно не утворювали прямокутник розміром
на такі ж кутики так, щоб жодні два такі триміно не утворювали прямокутник розміром  .
.
8. Якими видами тетраміно можна замостити дошку розміром 10´10?
9. Прямокутну клітчасту дошку зі стороною розміром m×n замощено плитками Т-тетраміно. Доведіть, що m і n діляться на 4.
10. а) Знайдіть усі такі натуральні числа n, що квадратну клітчасту дошку  можна було б замостити T-тетраміно. Відповідь обгрунтуйте. Подайте детальні пояснення. Розв’яжіть задачу декількома способами.
можна було б замостити T-тетраміно. Відповідь обгрунтуйте. Подайте детальні пояснення. Розв’яжіть задачу декількома способами.
б) Чи зміниться результат, якщо замість плоскої дошки замощувати циліндричну, тороїдальну?
11. а) Знайдіть усі такі натуральні числа n, що квадратну клітчасту дошку  можна було б замостити L-тетраміно. Відповідь обгрунтуйте. Подайте детальні пояснення. Розв’яжіть задачу декількома способами.
можна було б замостити L-тетраміно. Відповідь обгрунтуйте. Подайте детальні пояснення. Розв’яжіть задачу декількома способами.
б) Чи зміниться результат, якщо замість плоскої дошки замощувати циліндричну, тороїдальну?
12. а) З прямокутної клітчастої дошки  склеїли циліндр. При якій умові її можна замостити лінійним
склеїли циліндр. При якій умові її можна замостити лінійним  -міно?
-міно?
б) Якщо  , то з дошки
, то з дошки  можна склеїти два різних циліндри. Чи може статися так, що один з них можна замостити лінійним
можна склеїти два різних циліндри. Чи може статися так, що один з них можна замостити лінійним  -міно, а інший – ні?
-міно, а інший – ні?
13. Знайдіть усі такі пари натуральних чисел (m; n), що клітчасту дошку  можна було б замостити лінійним
можна було б замостити лінійним  -міно. Відповідь обгрунтуйте. Подайте детальні пояснення. Розв’яжіть задачу декількома способами.
-міно. Відповідь обгрунтуйте. Подайте детальні пояснення. Розв’яжіть задачу декількома способами.
14. Є прямокутна клітчаста дошка  і доміно. Пара різних клітинок називається "гарною", якщо фігуру F, одержану з дошки в результаті вирізання цих двох клітинок, можна замостити доміно. Знайдіть усі "гарні" пари клітинок дошки.
і доміно. Пара різних клітинок називається "гарною", якщо фігуру F, одержану з дошки в результаті вирізання цих двох клітинок, можна замостити доміно. Знайдіть усі "гарні" пари клітинок дошки.
15. Є прямокутна клітчаста дошка  і лінійне (пряме)
і лінійне (пряме)  -міно. Клітинку дошки (x, y) будемо називати "вдало розміщеною", якщо фігуру F, одержану з дошки в результаті вирізання цієї клітинки, можна замостити лінійним
-міно. Клітинку дошки (x, y) будемо називати "вдало розміщеною", якщо фігуру F, одержану з дошки в результаті вирізання цієї клітинки, можна замостити лінійним  -міно. Знайдіть множину М усіх вдало розміщених клітинок дошки.
-міно. Знайдіть множину М усіх вдало розміщених клітинок дошки.
16. Прямокутну клітчасту дошку (на якій клітчаста сітка є з двах сторін) перегнули і слеїли так, щоб одержати лист Мебіуса.
а) При якій умові лист Мебіуса замостити лінійним  -міно?
-міно?
б) Якщо  , то з клітчастої дошки
, то з клітчастої дошки  можна склеїти два листи Мебіуса. Чи може статися так, що один з них можна замостити лінійним
можна склеїти два листи Мебіуса. Чи може статися так, що один з них можна замостити лінійним  -міно, а інший – ні?
-міно, а інший – ні?
17. Є прямокутна клітчаста дошка  і натуральне число
і натуральне число  , де
, де 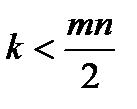 . Грають двоє. Перший гравець викреслює довільну клітинку дошки, потім другий гравець викреслює довільну клітинку, відмінну від викресленої; черговий хід гравця полягає у викреслюванні довільної клітинки, відмінної від раніше викреслених. Після того, як гравці зробили почергово по
. Грають двоє. Перший гравець викреслює довільну клітинку дошки, потім другий гравець викреслює довільну клітинку, відмінну від викресленої; черговий хід гравця полягає у викреслюванні довільної клітинки, відмінної від раніше викреслених. Після того, як гравці зробили почергово по  ходів, визначається переможець. Виграє другий, якщо фігура, одержана після вирізання всіх викреслених клітинок, може бути замощена доміно; у протилежному випадку переможцем вважається перший гравець.
ходів, визначається переможець. Виграє другий, якщо фігура, одержана після вирізання всіх викреслених клітинок, може бути замощена доміно; у протилежному випадку переможцем вважається перший гравець.
Знайдіть стратегію гри для одного із гравців, яка дозволить йому виграти незалежно від гри суперника.
18. Чи можна розв’язати загальну задачу про розрізання клітчастої прямокутної дошки на однакові клітчасті смужки довільної довжини?






