Модель перекрывающихся контрактов.

Неокейнсианская макроэк.школа.

Основные предположения:

1.Работники ведут себя в соответствии с концепцией рациональных ожиданий. Рациональность проявляется в том, что работники формируют свои прогнозы в соответствии с правилами взятия условных мат.ожиданий.

2.Ставка з/п фиксируется в трудовом договоре на некоторый период времени;

3.Не все работники заключают свои трудовые договоры одновременно. Считается, что работники делятся на 2 группы, группа А и группа Б. Все работники заключают трудовые договоры с руководством фирм, в кот они работают, сроком на 1 год. По истечении труд.договора заключается новый договор, условия кот могут отличатся от условий предыдущего. Работники групп А и Б различаются тем, что периоды действия их договоров не совпадают. Трудовые договоры работников группы А начинают и прекращают действовать первого января каждого года, а договоры работников группы Б – первого июля каждого года.

Введем следующие обозначения:

– ставка з/п по контракту, кот заключается в конце периода [t-1; t];

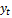– уровень нац.дохода;

– средняя з/п в экономике в целом;

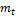- объем денежной массы (предложения) в экономике.

Все переменные модели изменяются в логарифмической шкале в отклонениях от тренда.

Единичным периодом в данной модели явл полугодие, т.к. в течение этого периода условия труда всех работников не изменяются.

Основное уравнение модели имеет вид:

, (1)

Где 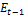– условное мат.ожидание, вычисленное в момент времени t-1, 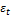- белый шум, . ( -прогноз).

Урав-ие (1) показыв., что при принятии решения о том, какой ур-нь з/п требовать при заключении нового контракта, работники каждой группы учитывают след.информ-цию:

1.Уровень з/п, кот добились работники другой группы на предыдущих торгах;

2.Прогноз уровня з/п, кот работники другой группы смогут добиться;

3.Прогнозы уровня нац.дохода в первом и втором полугодии наступающего года.

При этом величины и можно интерпретировать, как весовые коэффициенты, с помощью кот работники соизмеряют ценность прошлого и будущего дохода. Коэффициент показывает степень влияния информации о внешней среде относительно информации и внутренней среде фирмы на принятие решения.

Денежная масса пропорциональна нац.доходу, выраженному в текущих ценах. Т.к. в модели перекрывающихся контрактов переменные измеряются в логарифмической шкале, аналогичное соотношение будет иметь вид: (2) Предполагается, что -белый шум.

Средняя з/п определяется формулой: (3).

Наконец, имеет место след.правило монетарной политики: (4), где g – коэф.адаптации денежной массы к изменению уровня цен, 0<g<1.

Формулы (1)-(4) дают полное описание модели перекрывающихся контрактов.

Введем обозначение: .

Взяв от обеих частей уравнения (1) прогноз относительно момента t=0, получим:

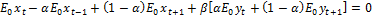(5).

Подставив уравн-ие (3) для средней з/п в формулу (2) и разрешив полученное уравн-ие относительно нац.дохода, получаем:

(6).

Переходя к прогнозным величинам, получаем: (7).

Подставив (7) для прогноза нац.дохода в (5), после преобразований придем к уравн-ю:

(8), здесь , .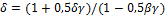

Уравн-ие (8) есть линейное однородное разностное уравнение второго порядка относительно прогнозов .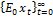

Характер.уравн-ие (8) равносильно уравнению: . Корни вещественны и положительны, а также .

Вместо t=0 можно выбрать любой другой момент времени, например, t-1, отсюда, при условии, что решение ограничено, следует равенство: (9). Сопоставляя (9) и (1), получим: 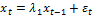. Подставляя данное выражение в (3) и (6), получаем формулы для средней ставки з/п и нац.дохода:

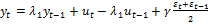; . Отсюда следует, что отклонения средней ставки з/п и нац.дохода от трендовых значений не явл белыми шумами. Они представляют собой процессы с четко выраженной автокорреляцией и потому являются прогнозируемыми.

 

42.Модель перекрывающихся поколений: случай производственной функции типа Кобба-Дугласа и логарифмических предпочтений.

Эта модель базируется на следующих предположениях:

1.Каждый эк.субъект живет в течение двух периодов; на протяжении первого периода он явл представителем молодого поколения, на протяжении второго – представителем старшего поколения.

2.Предложение труда формируется только за счет молодых агентов, а собственниками капитала явл только представители старшего поколения.

3.Технология произ-ва описывается неоклассической производств.ф-ей, и на рынках капитала и труда в каждый момент времени имеет место конкурентное равновесие.

4.Эк.агенты действуют рационально, т.е. в соответствии с принципами максимизации полезности, кот они могут получить в течение жизни.

5.Эк.агенты заботятся лишь о собственном благосостоянии и не интересуются судьбой потомков.

6.Население растет с постоянным экзогенно заданным темпом n.

Пусть эк.агент представляет молодое поколение периода t, а к наступлению периода t+1 переходит в группу представителей старшего поколения. Обозначим потребление этого агента в период t посредством 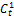, а его потребление в период t+1 – посредством 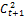. В силу предположения 2, доход, кот эк.агент получает, будучи молодым, это з/п. Обозначим размер з/п посредством , а ту часть дохода, кот не потребляется эк.агентом в течение его молодости и может интерпретироваться как сбережения «на старость», будем обозначать . Ясно, что должны выполняться естественные соотношения: , (1). В данной модели отсутствует условие неотрицательности величины . Ситуацию, когда , можно трактовать как заимствование.

На рынке капитала в течение каждого периода времени [t;t+1] действует % ставка 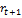. Если сбережения (заимствования) молодого агента равны , то его доход (обязательство) за второй период жизни составит (1+ 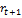) . Отсюда, в силу предположения о том, что весь капитал принадлежит старшему поколению, возникает ограничение на потребление представителей старшего поколения: (2).

В соответствии с 5 предположением, рациональный агент всегда будет потреблять весь свой доход в течение жизни. Поскольку период t+1 – второй и последний период жизни агента, родившегося в начале периода t, неравенство (2) в действительности должно выполняться как равенство: 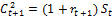(3).

Объединяя формулы (1) и (3), получаем: (4). Фор-ла (4) говорит о том, что приведенная ценность потока потребления агента в течение жизни равна его трудовому доходу, кот определяется размером ставки з/п .

В соответствии с 4 предположением каждый индивид должен максимизировать некот ф-ю полезности .

Примем допущение о том, что предпочтения эк.агентов описываются логарифмической ф-ей полезности: 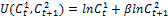(5), где - коэффициент дисконтирования, показывающий, насколько сильнее текущее потребление ценится по сравнению с будущим. Предполагается, что коэф-т дисконтир-ия удовлетворяет стандартному условию: .

Эк.агент принимает решение о разделении заработанных в молодости денег на потребление и сбережение, исходя из желания максимизировать функцию полезности (5) по множеству потоков потребления , удовлетворяющих условию (4). Следовательно, поведение агентов в молодости описывается как процесс решения следующей оптимизационной задачи:

(6)

(7)

Задачу (6)-(7) можно решить методом множителей Лагранжа. Составим ф-ю Лагранжа: 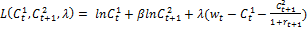. Необходимым условием оптимальности для задачи (6)-(7) явл равенство частных производных ф-ии Лагранжа нулю. , 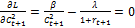. Разделив полученные равенства друг на друга, придем к соотношению: 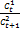= (8). Решая систему ур-ний (4) и (8) относительно в предположении, что з/п и % ставка заданы, можно ответить на вопрос о том, сколько агент будет потреблять «в молодости», а сколько – «в старости».

Теперь опишем производственно-технологическую сторону эк-ки. Пусть технология произв-ва описывается неоклассической производственной ф-ей , а кол-во молодых агентов увеличивается по закону геометрической прогрессии . Кроме того, будем считать, что осн.капитал служит в течение 1ого единичного периода, т.е. имеет место 100% износ. Тогда уравнение динамики капитала преобразуется к виду: (9). Ур-ние (9) получается из при 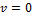с учетом того, что инвестиции равны произведению дохода всех молодых агентов и нормы сбережений .

Обозначим посредством R процентный множитель, соответствующий % ставке r: .

Используя выражения для предельных производительностей факторов как функций от фондовооруженности k, запишем условия конкурентного равновесия на факторных рынках: 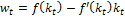(10), (11), где 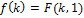-производственная ф-я в интенсивной форме. Подставляя (10) в (9) и разделив обе части полученного равенства на , получаем: (12). Ур-ние (12) есть нелинейное разностное ур-ние первого порядка.

Технология производства описывается производственной фун-ей типа Кобба-Дугласа.

Производственная ф-я в интенсивной форме, определяемая в общем случае формулой , в данной ситуации имеет вид: 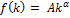(13). Параметры , 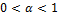. Используя (13), получаем, что для ф-ии Кобба-Дугласа предельная производительность труда определяется по формуле: (14). Подставляя (14) в правую часть уравнения динамики (12), имеем: (15), где . Стационарное значение фондовооруженности можно получить из (15): (16). Стационарное состояние ур-ния (16) глобально и локально устойчиво.