Где я использую фракталы и почему..

Про фракталы. Что это такое. Определение. Понятие. Виды. Салфетка и бла-юла кого-то.

Несмотря на широкое распространение, понятие фрактала до сих пор не имеет четкого и строгого определения. Наиболее простым и кратким определением фракталов является следующее: фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому. Однако это определение не дает полного представления о разнообразии объектов, которые относят к фракталам. Мандельброт определил фрактал (от латинского fractus — дробный) следующим образом: «фракталом называется множество, размерность Хаусдорфа- Безиковича которого строго больше его топологической размерности» (Мандельброт, 2002, с. 31) [44]. Это определение достаточно строго в математическом плане, однако именно это и является его существенным недостатком, поскольку оно требует определения еще и понятий размерности (топологической и хаусдорфо- вой), к тому же оно исключает многие классы фрактальных объектов, встречающиеся в различных областях естествознания. Мандельброту же принадлежит и более общая и менее формальная дефиниция: «Все фигуры, которые я исследовал и назвал фракталами, в моем представлении обладали свойством быть нерегулярными, но самоподобными» (Мандельброт, 2002) [44]. Таким образом, при характеристике фрактала центральным понятием оказывается самоподобие. Можно сказать, что фрактальный объект статистически единообразен в широком диапазоне масштабов. В идеальном случае (математический фрактал) такое самоподобие приводит к тому, что фрактальный объект оказывается инвариантным относительно масштабных изменений пространства (растяжений и сжатий).

В книге Фальконе [100] (Falconer, 1995) дано удачное сравнение: «Определить, что такое фракталы в математике столь же сложно, как и определить, что такое жизнь в биологии. Можно лишь перечислить некоторые свойства, которыми (не обязательно всеми) могут обладать эти объекты. Обычно, если говорят, что множество F является фракталом, то имеют в виду следующее:

1) F имеет тонкую структуру, т.е. детали произвольно малых масштабов.

2) F является слишком нерегулярным для того, чтобы описываться традиционной геометрией, как локально, так и глобально.

3) F обладает некоторым самоподобием, возможно приблизительным или статистическим.

4) Обычно как-либо определенная «фрактальная размерность» F больше, чем его топологическая размерность.

5) Во многих интересных случаях множество F определяется очень просто, возможно рекурсивно.»

Четвертое из этих свойств соответствует первоначальному определению, данному Б. Мандельбротом [145] (Mandelbrot, 1982), причем под фрактальной размерностью в этом определении подразумевалась размерность Хаусдорфа- Бези- ковича.

Главной количественной характеристикой фрактального объекта является его размерность [23]. Наиболее просто понятие размерности можно ввести как количество переменных (или измерений), необходимых для полного описания положения точки в пространстве. Так, для описания положения точки на плоскости необходимо указать две координаты, поэтому плоскость, также как и любая другая гладкая поверхность, имеет размерность, равную 2, то есть двумерна. Описать положение точки на линии можно с помощью одной координаты, поэтому линия одномерна, ее размерность равна 1. Аналогично, размерность точки равна нулю; пространство, в котором мы все живем, трехмерно. Введенное таким интуитивным образом понятие размерности соответствует тому, что в математике называется топологической размерностью. Эта размерность всегда является целым числом

Обратимся теперь к так

Называемой

триадной кривой Коха, впервые предложенной шведским математиком Хельге фон Кохом в 1904 году [51]. Алгоритм ее построения также начинается с прямолинейного отрезка единичной длины. Центральная треть отрезка вырезается, а на его месте надстраивается фиорд из двух отрезков, образующих с вырезанной частью равносторонний треугольник (рис. 1.2), получается фигура, сумма которой — ■ равна единице. Это означает, что полученное нами фрактальное множество — канторовское множество — не имеет длины.

Рассмотрим правую (или, если хотите, левую) треть нашего единичного отрезка подверженного итерационной генерации канторовского множества. Эта третья часть является уменьшенной (в три раза по линейным размерам) копией нашего канторовского множества и содержит при этом половину его массы (напомним, что третья часть, находящаяся в середине единичного отрезка попросту выброшена из него при генерации канторовского множества). Теперь все, что мы только являющаяся генератором нашего нового фрактала. На последующих шагах построения кривой Коха все прямолинейные отрезки просто заменяются уменьшенными копиями генераторами, то есть их средняя треть вырезается и заменяется фиордом. В результате бесконечного повторения такой несложной процедуры получается очень красивая фигура, любая сколь угодно малая часть которой подобна целой конструкции. Используя функциональное уравнение (1.1) мы легко можем определить фрактальную размерность ln(4)

кривой Коха: df = —— и 1.2619. Длина кривой Коха не определена: ее вели- ln(3)

чина зависит от точности измерения и расходится при увеличении этой точности. Действительно, на каждом шаге итерационной процедуры, представленной на рис. 1.2, длина образующейся ломаной увеличивается по сравнению с предыдущей в 4/3 раза и составляет (4/3)ⁿ, где n - номер шага процедуры.

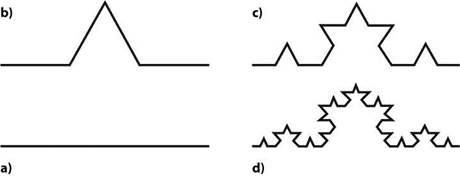Рис. 1.2. Изображение итерационной процедуры построения кривой Коха

Применим теперь описанную выше процедуру Коха сразу для трех отрезков, образующих равносторонний треугольник (см. рис. 1.3). На первом шаге итерационной процедуры мы получим звезду Давида, а затем снежинку, граница которой на каждом последующем шаге становится все более изрезанной. Эта фигура с фрактальной границей называется островом Коха.

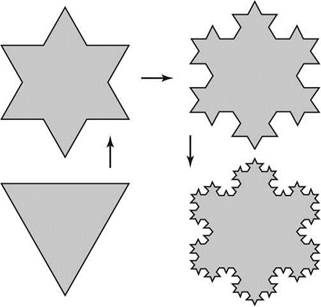
Рис. 1.3. Изображение итерационной процедуры построения острова Коха

Очевидно, что периметр острова Коха также как и длина кривой Коха зависит от точности его измерения и расходится при увеличении этой точности. На n-ом

■₄\ ⁿ

шаге итерационной процедуры периметр составляет P_n = 3 • (—

Найдем площадь острова Коха. На первом шаге процедуры площадь исходного равностороннего треугольника So = увеличивается за счет площади фиордов, выступающих с каждой из трех сторон. Очевидно, что площадь одного фиорда составляет одну девятую часть от площади исходного равностороннего треугольника, так что S₁ = S₀ + 3 ■ — ■ S₀. На каждом поседующем шаге процедуры площадь острова будет увеличиваться за счет площади новых фиордов, число которых с каждой стороны исходного треугольника будет расти как степень четверки, а площадь будет уменьшаться как степень одной девятой:

(1.6)

1 + t

4^ \9 i=1

1 4 4^n-1 Sn = So +3 ■ I 9 ■So + 9У- So +... + — -So) = So

В выражении (1.6) справа стоит сумма геометрической прогрессии со знаме- 4

нателем —, поэтому окончательно мы получаем

! -, 9 -

(1.7)

^Sn = ^So j ¹ + 5

При стремлении числа шагов процедуры к бесконечности мы найдем площадь острова Коха:

S =5 -So = ²|³. (1.8)

5 5

Мы получили интригующий результат — конечная площадь острова Коха ограничена периметром бесконечной длины.

Любопытно взглянуть на это еще и с другой стороны. Дело в том, что форма плоских фигур может быть охарактеризована краевым индексом:

^aEI = ^, т-1 ⁽¹.9)

2VпА

где P — полный периметр фигуры, включая внутренние границы, если таковые имеются, а А — площадь фигуры. Для круга, например, a_EI принимает минимальное возможное значение равное единице, для квадрата a_EI ~ 1, 29. Для острова Коха краевой индекс равен бесконечности!^

Ясно, что в реалиях физического мира мы никогда не встречаемся с такого рода бесконечностью. Тем не менее, как мы увидим в главе 3, природа очень часто обращается к подобным аномалиям для решения конкретных проблем.

^В трехмерном пространстве объемная фигура может быть охарактеризована поверхностным индексом

_ S ³ (врп • V)^2/3 ’

где S — полная площадь поверхности фигуры, включая внутренние границы, если таковые имеются, а V — объем фигуры. Для шара, например, аз принимает минимальное возможное значение равное единице, для куба аз ~ 1, 24.