Последовательность расчета следующая:
1. при последовательном соединении резисторов в отдельных ветвях находят их эквивалентное сопротивление;
2. при параллельном соединении резисторов находят их эквивалентное сопротивление;
3. при наличии соединения треугольником или звездой для упрощения схемы выполняют ее преобразование;
4. выполнив пункты 1, 2, 3 необходимое количество раз, находят эквивалентное сопротивление всей цепи;
5. по закону Ома находят ток в неразветвленной части цепи;
6. для расчета токов в остальных ветвях схему "разворачивают" в обратном порядке и по закону Ома находят токи.
Пример 1. Найти токи в схеме на рис.1.6а если: R1 =12 Ом, R2 = R3 =10 Ом, R4 =30 Ом, R5 = R6 =20 Ом, напряжение на входе цепи U =120 В.

а)

| 
|
| б) | в) |

г)
Рис. 1.6. Преобразования электрической цепи в примере 1
Решение. Задачу решаем методом эквивалентных преобразований. Резисторы R5 и R6 соединены параллельно. Их эквивалентное сопротивление R56 равно  Ом.
Ом.
После преобразования схема принимает вид рис.1.6б. В ней резисторы R4 и R56 соединены последовательно. Их эквивалентное сопротивление R456= R4+R56=30+10 =40 Ом.
Резисторы R3 и R456 соединены параллельно, Их эквивалентное сопротивление R3456 равно R3456= R3 R456/(R3+ R456) = 400/50=8 Ом.
Резисторы R1, R2 и R3456 соединены последовательно. Их эквивалентное сопротивление R123456, а, следовательно, и эквивалентное сопротивление всей цепи Rэкв равно R123456 = Rэкв = R1+ R2 + R3456 =12+8+10=30 Ом.
Далее найдем токи во всех ветвях схемы.
Ток в неразветвленной части I1 равен I1= U/Rэкв =4 А.
Для расчета токов I3 и I4 определим напряжение на участке ав по закону Ома: U ав= I1 R3456 =4.8=32 В.
Отсюда ток I3= Uав/R3 =32/10=3,2 А, а ток I4= Uав/ R456 =32/40=0,8 А.
Для расчета токов I5 и I6 определим напряжение на участке cd по закону Ома: U cd= I4 R56 =0,8.10 =8 В. Отсюда ток I5 = Ucd/R5 =8/20=0,4 А, а ток I6 = Ucd/ R6 =8/20=0,4 А.
Итак, все токи найдены.
Пример 2. Пусть требуется рассчитать цепь, показанную на рис.1.7а, при следующих числовых значениях ее параметров: Е = 660 В, R 1 = 20 Ом, R 2 = 30 Ом, R 3 = 5 Ом, R 4 = 20 Ом, R 5 = 50 Ом.

Рис. 1.7. Преобразования электрической цепи в примере 2
Попытка определить общее сопротивления цепи на рис.7, не зная правил эквивалентного преобразования треугольника в звезду и наоборот, оказывается безрезультатной, так как здесь мы не находим ни последовательно, ни параллельно соединенных сопротивлений. Решить задачу помогает преобразование треугольника сопротивлений в эквивалентную звезду.
Решение. Решение выполняем преобразованием треугольника в звезду.
После преобразования треугольника, образованного сопротивлениями R 1, R 2 и R 5, в звезду, получаем схему, показанную на рис.1.7б. Обращаем внимание на то, что токи в непреобразованной части схемы (I, I 3 и I 4) остались теми же.
Сопротивления звезды определяем по сформулированному выше правилу:
 Ом;
Ом;  Ом;
Ом; 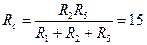 Ом.
Ом.
Теперь общее сопротивление цепи легко находится:
 Ом.
Ом.
Ток, протекающий по источнику (одинаковый в заданной и преобразованной схемах), равен
 А.
А.
Токи в параллельных ветвях:
 28 A;
28 A;  12 A.
12 A.
Возвращаемся к исходной схеме (рис.1.7а) и находим:
 26 A;
26 A;  14 A.
14 A.
Ток в пятой ветви находим из первого закона Кирхгофа: I 5 = I 1 – I 3 = 26 –2 8 = –2 A. Знак минус говорит о том, что действительное направление тока I 5противоположно указанному на схеме.






