Эквивалентные преобразования резисторов в цепях постоянного тока
Методические указания к лабораторной работе
по дисциплине “Электротехника”
Казань 2009
Цель работы -опытная проверка правил эквивалентного преобразования резисторов при последовательном, параллельном и смешанном соединениях, а также преобразования треугольника резисторов в эквивалентную звезду и наоборот. Применение метода эквивалентных преобразований для расчета электрических цепей постоянного тока.
Основные понятия и расчетные соотношения
ОБЩИЕ СВЕДЕНИЯ
Применение законов Ома и Кирхгофа позволяет преобразовать сложные электрические цепи в более простые, заменяя отдельные участки цепи, содержащие несколько элементов, одним эквивалентным элементом. Таким образом, эквивалентные преобразования позволяют заменить исходную цепь, содержащую большое число элементов, более простой, с меньшим числом элементов, но эквивалентной исходной цепи.
Цепи считаются эквивалентными, если при их взаимной замене токи и напряжения на интересующих нас участках цепи остаются неизменными.
ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ ПРИ ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ РЕЗИСТОРОВ
Последовательное соединение нескольких резисторов можно заменить одним резистором с сопротивлением R ЭКВ (рис. 1.1).
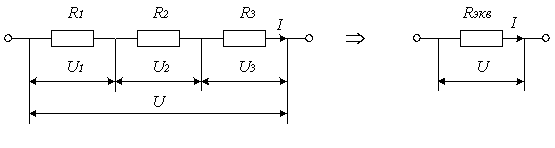
Рис.1.1. Последовательное соединение сопротивлений
По второму закону Кирхгофа напряжение U складывается из падений напряжения на каждом из резисторов R1, R2, и R3, т.е.
| U = U1 +U2 +U3. | (1.1) |
Так как ток I является одинаковым для всех резисторов, то (1.1) можно записать в виде
 ,
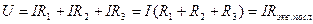| (1.2) |
откуда
 .
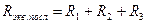| (1.3) |
В общем виде эквивалентное сопротивление при последовательном соединении элементов цепи равно сумме сопротивлений отдельных элементов:
 ,
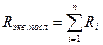| (1.4) |
где n - число резисторов.
Пример: Определить эквивалентное сопротивление цепи из трех резисторов (R1 = 1 Ом, R2 =2 Ом и R3 =3 Ом) соединенных последовательно.
По формуле (1.4) получаем RЭКВ =6 Ом.
При последовательном соединении резисторов их эквивалентное сопротивление всегда больше большего из сопротивлений этих резисторов.
При последовательном соединении резисторов ток в цепи одинаков:
 .
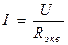| (1.5) |
Напряжение Ui и мощность Pi на зажимах последовательно соединенных элементов распределяется пропорционально их сопротивлениям, т. к. Ui = IRi,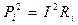 
, а мощность, подводимая к цепи, равна сумме мощностей на отдельных элементах:
 .
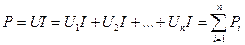| (1.6) |
ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ ПРИ ПАРАЛЛЕЛЬНОМ СОЕДИНЕНИИ РЕЗИСТОРОВ
При параллельном соединении резисторов (рис.1.2) все элементы цепи, в том числе и эквивалентное сопротивление RЭКВ пар находятся под одним и тем же напряжением U.
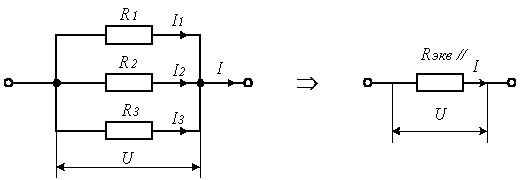
Рис.1.2. Параллельное соединение сопротивлений
Для цепи (рис. 2) по первому закону Кирхгофа
| I = I1+ I2 + I3, | (1.7) |
где по закону Ома
 .
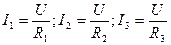| (1.8) |
В то же время для эквивалентной схемы
 .
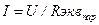| (1.9) |
Подставляя значения токов (1.8) и (1.9) в (1.7) и сокращая на U, получим
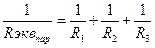. (1.10)
В общем случае для n резисторов при параллельном соединении
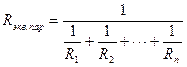. (1.11)
Для двух резисторов соединенных параллельно эквивалентное сопротивление записывают так:
 .
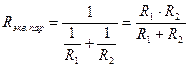| (1.12) |
Пример: Определить эквивалентное сопротивление цепи из трех резисторов (R1 = 3 Ом, R2 =3 Ом и R3 =3 Ом) соединенных последовательно.
По формуле (1.10) получаем RЭКВ=1 Ом.
При параллельном соединении резисторов их эквивалентное сопротивление всегда меньше меньшего из сопротивлений этих резисторов.
При параллельном соединении элементов часто пользуются не сопротивлениями элементов, а их проводимостью. Как известно электрической проводимостью, называется величина, обратная сопротивлению. Она обозначается G и измеряется в сименсах (См); 1См = 1 / 1 Ом.
Тогда уравнение (1.10) можно переписать для проводимостей как:
| Gэкв пар = G1 + G2 + G3, | (1.13) |
или в общем виде для n – резисторов
 .
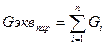| (1.14) |
Следовательно, при параллельном соединении элементов электрической цепи эквивалентная проводимость равна сумме проводимостей ее отдельных параллельно включенных ветвей.
Ток в параллельных ветвях цепи, согласно (1.8), распределяется обратно пропорционально их сопротивлениям.
Напряжение на всех элементах параллельной цепи одинаково и определяется выражением (1.15):
 .
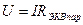| (1.15) |
Мощность, подводимая к цепи с параллельно включенными резисторами, равна сумме мощностей ее отдельных элементов:
 .
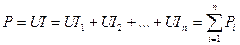| (1.16) |
