В электронных таблицах имеется около 50 функций, специально предназначенных для финансовых расчетов. В данной работе рассмотрим вычисления, связанные с начислением процентов.
Пусть на срок t предоставлена в кредит некоторая сумма Р. За использование кредита надо платить. Возврат кредита составит S=P+I. Плата I носит название “процент”. Чем больше время, на которое выдается кредит, тем больше процент. В простейшем случае полагают
I = P× r × t,
где r – процентная ставка.
Величина наращенной суммы для схемы простых процентов (когда проценты начисляются каждый период на начальную сумму кредита) определяется по формуле
S = P + I = P + P× r ×t = P (1 + r × t). (1)
Для схем сложных процентов (когда процент начисляется на наращенную сумму, полученную за предыдущий период) используется формула
S=P (1+ r) t. (2)
Большинство финансовых функций используют эти формулы.
Порядок выполнения работы
Задание 1. Вычислить размер возвращаемой ссуды, используя формулу (1).
Задание 2. Вычислить размер возвращаемой ссуды, используя финансовую функцию для вычисления будущего значения.
В Excel это функция БC (будущая сумма), в табличном процессоре Calc- функция FV (Futurum Value).
Задание 3. Вычислить размер возвращаемой ссуды по схеме сложных процентов.
Задание 4. Рассчитать постоянную ренту, используя функцию БС (будущая сумма).
Задание 5. Используя функцию ПС (приведенная или современная Сумма), рассчитать сумму денег, которую можно получить под вексель.
Задание 6. Рассчитать срок вклада, необходимый для наращения нужной суммы.
Задание 7. Рассчитать процентную ставку кредита.
Выполнение задания 1
Рассмотрим порядок вычисления размера возвращаемой ссуды на следующем примере. В примере 1 и далее приведены фрагменты табл. 13.
ПРИМЕР 1
Ссуда в размере 1 млн долларов выдана 5 января 2008 г. по 20 сентября 2008 г. включительно. Годовая процентная ставка – 15 %. Какую сумму придется заплатить должнику в конце срока?
РЕШЕНИЕ
Процентная ставка дана годовая, но срок ссуды меньше, значит, следует пересчитать ставку (или период), на который выдана ссуда. Произведем расчеты в электронной таблице.
3.1.1.Ввод исходных данных в таблицу
В ячейки А1:В8 введите текст и исходные данные задачи.
Внимание! При вводе в ячейку В8 суммы кредита $1000000, сначала следует, поставив курсор в ячейку В8 выполнить команды Формат – Ячейки, в появившемся окне выбрать вкладку Числа, Числовые форматы: Денежный, Обозначение $ Английский (США), ОК. Затем в ячейку В8 ввести число 1000000.
3.1.2. Расчет доли года. Ввод комментариев
Для пересчета процентной ставки нужно знать, какую долю года составит срок кредита. В ячейку В10 введите формулу =В7-В6. Установите для ячейки В10 числовой формат.
В ячейке В10 появится результат – 258 (период вклада в днях). Произведем пересчет в долях года, для этого в ячейку В11 введите формулу =В10/366. Итог расчета дает 0,71 года.
Для наглядности в столбец С введите комментарии – те же формулы из смежных ячеек столбца В, но перед знаком = вводите знак апостроф (одинарная кавычка). Например: ‘= В7 – В6. В столбце С вычисления производиться не будут.
3.1.3. Расчет процентной ставки
В ячейку В12 введите формулу для пересчета процентной ставки =В5*В11. Ставка за период составила 11, а не 15 %. Теперь при подстановке значений в формулу (1) нужно брать либо рассчитанную долю года, либо 11 % вместо 15.
3.1.4. Расчет суммы возврата
По формуле (1) наращенная сумма равна
S=P (1+ rt)=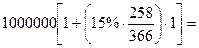 
1 106 027.
Здесь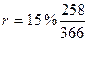 
; t = 1.
Введите в ячейку В13 формулу =В8*(1+B5*В11) для расчета возвращаемой суммы, используя формулу (1).
Таблица 13
| А | В | С | |
| ФИНАНСОВЫЕ ВЫЧИСЛЕНИЯ В Excel | |||
| Задание 1.Расчет возвращаемой суммы при получении кредита | |||
| Исходные данные | |||
| Переменные | Вычисления | Формулы и комментарии | |
| Годовая ставка | 15% | ||
| Дата выдачи кредита | 05.01.08 | ||
| Дата возврата кредита | 20.09.08 | ||
| Сумма кредита | $1 000 000 | ||
| Расчеты | |||
| Срок кредита в днях | ‘=В7-В6 | ||
| Срок кредита в годах | 0,71 | ‘=В10/366 | |
| Ставка для периода | 11% | ‘=В5*В11 | |
| Сумма возврата | $1 106 027,4 | ‘=В8*(1+В5*В11) |
Выполнение задания 2
3.2.1. Описание функции для вычисления будущего значения
Вычисления для примера 1 можно осуществить гораздо проще, если использовать в Excel финансовую функцию БС (будущая сумма). Ее синтаксис имеет вид:
=БС(Ставка; Кпер; Плт; ПС; Тип),
где
Ставка – процентная ставка за период;
Кпер – число периодов начисления процентов;
Плт (Промежуточные выплаты) – вводится, если имеются промежуточные выплаты;
ПС (приведенное или начальное значение) – размер кредита;
Тип – вводится равным единице, если промежуточные выплаты производят в начале периода, и равным нулю (или вообще не вводится), если выплаты производят в конце периода.
В программе OpenOffice.org Calc функция, аналогичная функции БС в Ехсе1, называется FV. Ее синтаксис имеет вид:
= FV(Процент; КПЕР; Выплата; ТЗ; Тип).
Здесь все аргументы имеют те же значения, что у функции БС:
Процент -процентная ставка за период;
КПЕР -количество периодов;
ТЗ – текущее значение (размер кредита).
Примечание! Следует иметь в виду, что функцию БС (В программе Calc- функцию FV) можно использовать для расчета по схеме простых процентов только в том случае, если начисление процентов проводится только за один период.
3.2.2. Вызов функции вычисления будущего значения
Активизируйте ячейку В16, затем щелкните по пиктограмме Мастер функций. В окне Категория выберите Финансовые, а в окне Функция выберите БС (FV) и щелкните ОК (Далее).
3.2.3. Ввод аргументов
· в поле Ставка (Процент) введите В12;
· в поле Кпер (КПЕР) – введите 1;
· поле Плт (Выплата) пропустите;
· в поле Пс (ТЗ)(начальное значение) – введите В8.
В результате в ячейке В16 появится такая же сумма, что и в ячейке В13, но со знаком минус.
Обратите внимание! В финансовых функциях Excel, если сумму отдают, то она отображается со знаком минус, а если получают то со знаком плюс.
Расчеты в Excel
| А | В | С | |
| Задание 2. Расчет возврата ссуды с использованием функции БС | |||
| - $1 106 027,4 | ‘=БС(В12;1;;В8) |
Расчеты в Calc
| А | В | С | |
| Задание 2. Расчет возврата ссуды с использованием функции FV | |||
| - $1 106 027,4 | ‘=FV(В12;1;;В8) |
Выполнение задания 3
ПРИМЕР 2
В банк на 5 лет помещен вклад в размере 50 000 руб. под 12 % годовых с ежеквартальным начислением. Какую сумму получит вкладчик через 5 лет?
РЕШЕНИЕ
В условии приведена годовая ставка, но начисление процентов ведется каждый квартал. Значит, процентная ставка за период равна
.
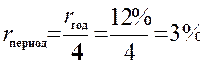Число периодов равно числу кварталов за 5 лет, т.е. 5*4=20.
Значит, по формуле (2) получим
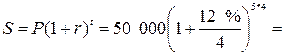90 305,56 руб.
3.3.1. Ввести в строку 17 комментарий к примеру
Расчет в Excel
| A | B | C | |
| Задание 3. Расчет по схеме сложных процентов | |||
| 90 305,56р. | ‘=БС(12%/4;5*4;;-50000) |
Расчет в Calc
| A | B | C | |
| Задание 3. Расчет по схеме сложных процентов | |||
| 90 305,56р. | ‘=FV(12%/4;5*4;;-50000) |
3.3.2. В ячейку В18 ввести формулу для вычисления наращенной суммы (аналогично пп. 3.2.2): =БС(12%/4;5*4;;-50000).
В программе OpenOffice.org Calc формула имеет вид: =FV(12%/4;5*4;;-50000).
3.3.3. В ячейку С18 ввести ту же формулу с апострофом (комментарий).
Выполнение задания 4
Финансовые схемы с многократными взносами или выплатами называются Постоянными рентами.
ПРИМЕР 3
На счет в банке вносят сумму $ 20 000 в течение 10 лет равными долями в конце каждого года. Годовая ставка равна 22 %. Какая сумма будет на счете по истечении 10 лет?
РЕШЕНИЕ
3.4.1. Ввод исходных данных в таблицу
Введите в ячейки А20:В25 текст и исходные данные из табл. 13.
3.4.2. Использование функции БС и ввод аргументов
В ячейку В27 введите формулу для расчета накопленной суммы при взносах в конце периода. Для этого:
· активизируйте ячейку В27;
· щелкните по пиктограмме Мастер функций;
· выберите в списке категорий функций Финансовые;
· выберите в списке финансовых функций – функцию БС( В программе OpenOffice.org Calc - FV);
· в поле Ставка (Процент) введите В25;
· в поле Кпер введите 10;
· в поле Плт (Выплата) введите –2000 (знак минус означает, что деньги отдают);
· остальные поля в данном случае пропускаются;
· щелкните ОК.
3.4.3. Расчет накопленной суммы при взносах в начале периода
· активизируйте ячейку В28;
· щелкните по пиктограмме Мастер функций;
· выберите в списке категорий функций Финансовые;
· выберите в списке финансовых функций – функцию БС (FV);
· щелкните ОК;
· в поле Ставка (Процент) введите В25;
· в поле Кпер введите 10;
· в поле Плт (Выплата) введите –2000 (знак минус означает, что деньги отдают);
· поле Пс пропустите;
· в поле Тип введите 1, так как выплаты производят в начале периода;
· щелкните ОК.
По результатам расчетов видно, что накопленная сумма в последнем случае выше.
Расчеты в Excel
| А | B | C | |
| Задание 4. Расчет постоянной ренты с использованием функции БС | |||
| Исходные данные | |||
| Переменные | Вычисления | Формулы и комментарии | |
| Срок | |||
| Сумма | $20 000 | ||
| Годовая ставка | 22% | ||
| Расчеты | |||
| Плата в конце периода | $57 314,83 | ‘=БС(В25;10;-2000) | |
| Плата в начале периода | $69 924,09 | ‘=БС(В25;10;-2000;;1) |
Расчеты в Calc
| А | B | C | |
| Задание 4. Расчет постоянной ренты с использованием функции FV | |||
| Исходные данные | |||
| Переменные | Вычисления | Формулы и комментарии | |
| Срок | |||
| Сумма | $20 000 | ||
| Годовая ставка | 22% | ||
| Расчеты | |||
| Плата в конце периода | $57 314,83 | ‘=FV(В25;10;-2000) | |
| Плата в начале периода | $69 924,09 | ‘=FV(В25;10;-2000;;1) |
Выполнение задания 5
В финансовых вычислениях часто решают задачу, обратную описанной в примере 1. Рассмотрим следующий пример.
ПРИМЕР 4
Вексель на 4 млн долларов с процентной ставкой 18 % и начислением процентов дважды в год выдан на три года. Найти исходную сумму, выданную под этот вексель.
РЕШЕНИЕ
Для решения этой задачи в Excel используют функцию ПС (приведенная или современная сумма). Синтаксис этой функции
=ПС(Ставка; Кпер; Плт; БС; Тип).
Все аргументы этой функции те же, что и у функции БС, только четвертым аргументом стоит не начальное, а будущее значение.
В программе OpenOffice.org Calc функция, аналогичная функции ПС в Ехсе1, называется РV IPresent Value). Ее синтаксис имеет вид:
= РV(Процент; КПЕР; Выплата; БЗ; Тип).
3.5.1. Ввод исходных данных
Введите в ячейки А30:В36 текст и исходные данные из табл. 13.
3.5.2. Вычисление процентной ставки за период
В задании приводится годовая учетная ставка, а начисление процентов ведется дважды в год. Поэтому в ячейку В38 введите формулу, вычисляющую процентную ставку за полгода =В33/В34.
3.5.3. Вычисление исходной суммы, выданной по векселю
· активизируйте ячейку В39;
· щелкните по пиктограмме Мастер функций;
· выберите в списке категорий функций Финансовые;
· выберите в списке финансовых функций функцию ПС;
· щелкните ОК;
· в поле Ставка(Процент) введите В38;
· в поле Кпер введите В34*В36;
· поле Плт (Выплата) пропустите (промежуточных выплат нет);
· в поле БС (БЗ) введите В35;
· поле Тип пропустите;
· щелкните ОК.
Расчеты в Excel
| А | В | С | |
| Задание 5. Расчет платы за вексель с использованием функции ПС | |||
| Исходные данные | |||
| Переменные | Вычисления | Формулы и комментарии | |
| Процентная ставка | 18% | ||
| Периодичность выплат | |||
| Будущее значение | -$4 000 000 | ||
| Количество лет | |||
| Расчеты | |||
| Процент за период | 9% | ‘=В33/В34 | |
| Современное значение | $2 385 069,31 | ‘=ПС(В38;В34*В36;;В35) |
Расчеты в Calc
| А | В | С | |
| Задание 5. Расчет платы за вексель с использованием функции PV | |||
| Исходные данные | |||
| Переменные | Вычисления | Формулы и комментарии | |
| Процентная ставка | 18% | ||
| Периодичность выплат | |||
| Будущее значение | -$4 000 000 | ||
| Количество лет | |||
| Расчеты | |||
| Процент за период | 9% | ‘=В33/В34 | |
| Современное значение | $2 385 069,31 | ‘=PV(В38;В34*В36;;В35) |
В результате в ячейке В39 появилось значение 2 385 069,32. Итак, под вексель 4 млн долларов можно получить сумму $2 385 069.
Выполнение задания 6
Обратимся к задаче определения продолжительности срока ссуды при заданных современном, будущем значениях и процентной ставки.
ПРИМЕР 5
За какой срок сумма, равная 80 рублям, достигает 300 000 рублей при начислении процентов по ставке 15 % раз в году и поквартально?
РЕШЕНИЕ
Воспользуемся функцией КПЕР (количество периодов). Ее синтаксис:
=КПЕР(Ставка;Плт; ПС; БС; Тип).
Все аргументы этой функции известны из предыдущих заданий.
В программе OpenOffice.org Calc функция, аналогичная функции КПЕР в Ехсе1, называется NРER. Ее синтаксис имеет вид:
= NРER(Процент; Выплата; ТЗ;БЗ; Тип).
3.6.1. Ввод заголовка примера 5 (см. табл. 13).
3.6.2. Определение числа периодов в годах при начислении процентов раз в году
· активизировать ячейку В42;
· щелкните по пиктограмме Мастер функций;
· выберите в списке категорий функций Финансовые;
· выберите в списке финансовых функций функцию КПЕР(NРER);
· щелкните ОК (Далее);
· в поле Ставка (Процент) введите 15 %;
· в поле Плт (Выплата) введите 0 (или пропустите);
· в поле ПС (ТЗ) введите –80 (знак минус – так как отдаем деньги);
· в поле БС (БЗ) введите 300000;
· поле Тип пропустите;
· щелкните ОК.
В результате вычислений период накопления заданной суммы составит 59 лет.
Расчеты в Excel
| А | В | С | |
| Задание 6. Расчет срока вклада с использованием функции КПЕР | |||
| Начисление раз в год | ‘=КПЕР(15%;0;-80;300000) | ||
| По кварталам | ‘=КПЕР(15%/4;0;-80;300000)/4 |
Расчеты в Calc
| А | В | С | |
| Задание 6. Расчет срока вклада с использованием функции NPER | |||
| Начисление раз в год | ‘=NPER(15%;0;-80;300000) | ||
| По кварталам | ‘=NPER(15%/4;0;-80;300000)/4 |
3.6.3. Определение числа периодов в годах при начислении процентов поквартально
· активизируйте ячейку В43;
· щелкните по пиктограмме Мастер функций;
· выберите в списке категорий функций Финансовые;
· выберите в списке финансовых функций функцию КПЕР (NРER);
· щелкните ОК (Далее);
· в поле Ставка (Процент) введите 15%/4 (начисление процентов производят четыре раза в год и за каждый квартал ставка в четыре раза меньше);
· в поле Плт (Выплата) введите 0 (или пропустите);
· в поле ПC (ТЗ) введите –80 (знак минус – отдаем);
· в поле БC (БЗ) введите 300000;
· поле Тип пропустите;
· щелкните ОК.
В ячейке В43 введена формула =КПЕР(15%/4;0;-80;300000) (в программе OpenOffice.org Calc -функция=NРER(15%/4;0;-80;300000), которая вычисляет рассчитываемое число периодов в кварталах, а нас интересует срок накоплений в годах.
3.6.4. Редактирование формулы расчета числа периодов
· активизируйте ячейку В43;
· установите курсор в строке формул в конец выражения и после скобки наберите с клавиатуры /4 (см. табл. 13);
· нажмите Enter.
В результате вычисляется, что период накопления заданной суммы составит 56 лет.
Вывод: при начислении процентов по кварталам срок накопления заданной суммы меньше, чем при ежегодном начислении.
Выполнение задания 7
ПРИМЕР 6
В долг на 4 года предоставлена ссуда $ 4000 с условием возврата $ 6000. Определить процентную ставку ссуды.
РЕШЕНИЕ
Для расчета процентной ставки используется функция
=СТАВКА (Кпер; Плт; ПС; БС; Тип; Предположение).
Здесь аргумент Предположение вводится, если можно сделать предположение о значении процентной ставки. В противном случае этот аргумент опускается.
В программе OpenOffice.org Calc функция, аналогичная функции СТАВКА в Ехсе, называется RАТE. Ее синтаксис имеет вид:
= RАТE(Кпер; Выплата; ТЗ; БЗ; Предположение).
3.7.1. В строку 45 ввести заголовок примера (см. табл. 13).
3.7.2. В ячейку В46 ввести формулу для расчета процентной ставки:
· Вставка – Функция – Финансовые – Ставка (RАТE) – Ок (Далее);
· ввести аргументы согласно табл. 12.
В программе OpenOffice.org Calc формула имеет вид:
= RАТE(4; 4000; -6000).
3.7.3. В ячейку С46 ввести ту же формулу с апострофом для комментария.
В результате вычислений у нас сформирована табл. 13.
При работе с программой Calc итоговые вычисления имеют вид табл. 14.
Самостоятельная работа
Рассчитайте значение вклада 5 000 долларов через 4 года при годовой процентной ставке 28 % с начислением процентов раз в полгода.
Отчет по работе
Распечатка итоговой таблицы и результатов самостоятельной работы.
Литература: [6], с. 261-271.
Таблица 13. Финансовые вычисления в Excel
| А | В | С | |
| ФИНАНСОВЫЕ ВЫЧИСЛЕНИЯ В Excel | |||
| Задание 1.Расчет возвращаемой суммы при получении кредита | |||
| Исходные данные | |||
| Переменные | Вычисления | Формулы и комментарии | |
| Годовая ставка | 15% | ||
| Дата выдачи кредита | 05.01.08 | ||
| Дата кредита | 20.09.08 | ||
| Сумма возврата | $1 000 000 | ||
| Расчеты | |||
| Срок кредита в днях | ‘=В7-В6 | ||
| Срок кредита в годах | 0,71 | ‘=В10/366 | |
| Ставка для периода | 11% | ‘=В5*В11 | |
| Сумма возврата | $1 106 024.4 | ‘=В8*(1+В5*В11) | |
| Задание 2. Расчет возврата ссуды с использование функции БС | |||
| $1 106 024.4 | ‘=БС(В12;1;;В8) | ||
| Задание 3. Расчет по схеме сложных процентов | |||
| 90305,56р. | ‘=БС(12%/4;5*4;;-50000) | ||
| Задание 4. Расчет постоянной ренты с использованием функции БС | |||
| Исходные данные | |||
| Переменные | Вычисления | Формулы и комментарии | |
| Срок | |||
| Сумма | $20 000 | ||
| Годовая ставка | 22% | ||
| Расчеты | |||
| Плата в конце периода | $57314,83 | ‘=БС(В25;10;-2000) | |
| Плата в начале периода | $69924,09 | ‘=БС(В25;10;-2000;;1) | |
| Задание 5. Расчет платы за вексель с использованием функции ПС | |||
| Исходные данные | |||
| Переменные | Вычисления | Формулы и комментарии | |
| Процентная ставка | 18% | ||
| Периодичность выплат | |||
| Будущее значение | -$4 000000 | ||
| Количество лет | |||
| Расчеты | |||
| Процент за период | 9% | ‘=В33/В34 | |
| Современное значение | $2 385 069,31 | ‘=ПС(В36;В34*В36;;В35) | |
Окончание табл. 13
| А | В | С | |
| Задание 6. Расчет срока вклада с использованием функции КПЕР | |||
| Начисление раз в год | ‘=КПЕР(15%;0;-80;300000) | ||
| По кварталам | ‘=КПЕР(15%/4;0;-80;300000)/4 | ||
| Задание 7. Расчет процентной ставки | |||
| 11% | ‘=СТАВКА(4;;4000;-6000) |
Таблица 14. Финансовые вычисления в Calc
| А | В | С | |
| ФИНАНСОВЫЕ ВЫЧИСЛЕНИЯ В Calc | |||
| Задание 1.Расчет возвращаемой суммы при получении кредита | |||
| Исходные данные | |||
| Переменные | Вычисления | Формулы и комментарии | |
| Годовая ставка | 15% | ||
| Дата выдачи кредита | 05.01.08 | ||
| Дата кредита | 20.09.08 | ||
| Сумма возврата | $1 000 000 | ||
| Расчеты | |||
| Срок кредита в днях | ‘=В7-В6 | ||
| Срок кредита в годах | 0,71 | ‘=В10/365 | |
| Ставка для периода | 11% | ‘=В5*В11 | |
| Сумма возврата | $1 106 024.4 | ‘=В8*(1+В5*В11) | |
| Задание 2. Расчет возврата ссуды с использование функции FV | |||
| $1 106 024.4 | ‘=FV(В12;1;;В8) | ||
| Задание 3. Расчет по схеме сложных процентов | |||
| 90 305,56р. | ‘=FV(12%/4;5*4;;-50000) | ||
| Задание 4. Расчет постоянной ренты с использованием функции FV | |||
| Исходные данные | |||
| Переменные | Вычисления | Формулы и комментарии | |
| Срок | |||
| Сумма | $20 000 | ||
| Годовая ставка | 22% | ||
| Расчеты | |||
| Плата в конце периода | $57 314,83 | ‘=FV(В25;10;-2000) | |
| Плата в начале периода | $69 924,09 | ‘=FV(В25;10;-2000;;1) | |
| Окончание табл. 14 | |||
| Задание 5. Расчет платы за вексель с использованием функции PV | |||
| Исходные данные | |||
| Переменные | Вычисления | Формулы и комментарии | |
| Процентная ставка | 18% | ||
| Периодичность выплат | |||
| Будущее значение | -$4 000 000 | ||
| Количество лет | |||
| Расчеты | |||
| Процент за период | 9% | ‘=В33/В34 | |
| Современное значение | $2 385 069,31 | ‘=PV(В36;В34*В36;;В35) | |
| Задание 6. Расчет срока вклада с использованием функции NPER | |||
| Начисление раз в год | ‘=NPER(15%;0;-80;300000) | ||
| По кварталам | ‘=NPER(15%/4;0;-80;300000)/4 | ||
| Задание 7. Расчет процентной ставки | |||
| 11% | ‘=RATE(4;;4000;-6000) |
