ФАЗОВА РІВНОВАГА В ОДНОКОМПОНЕНТНИХ СИСТЕМАХ
Завдяки тепловому руху молекули конденсованої фази (твердої речовини або рідини) можуть відриватися від її поверхні і переходити в газову фазу. Такий відрив можливий, якщо кінетична енергія молекули більше енергії взаємного зв'язку між молекулами конденсованої фази.
Частина молекул, що відірвалися від поверхні конденсованої фази, згодом знову конденсується, інша ж частина залишається в газоподібній фазі. Таким чином, на поверхні конденсованої фази завжди відбуваються одночасно протилежно направленні процеси випарування і конденсації. У замкнутому просторі поступово відбувається вирівнювання значень швидкості цих процесів. Між конденсованою й газоподібною фазами наступає стан динамічної рівноваги. Пара, що знаходиться в рівновазі з конденсованою фазою, називається насиченою парою, а тиск, що вона створює називається тиском насиченої пари. Тиск насиченої пари кожної стабільної хімічної речовини визначається тільки температурою. За допомогою цієї величини можна ідентифікувати речовини, визначати чистоту хімічних сполук.
Залежність тиску насиченої пари від температури виражається рівнянням Клапейрона-Клаузіуса
, (2.1)
де ΔH - теплота випарування, Дж/моль; ΔV - зміна об'єму при переході 1 моля конденсованої фази у пару, м3/моль.
Для розрахунку ΔH потрібні данні про мольні об'єми пари й конденсованої фази в умовах рівноваги. Ці дані відомі для невеликої кількості речовин, а експериментальне їх вимірювання пов'язане зі значними труднощами. Тому це рівняння спрощують, зробивши наступні припущення:
1. Vп >> Vк.ф., тому можна зневажити величиною Vк.ф і ΔV = Vп.
2. Рівняння стану пари підкоряється рівнянню стану ідеального газу, тобто pVп = RT.
3. Теплота випарування не залежить від температури, тобто ΔH = const.
З урахуванням цих припущень рівняння (2.1) перетвориться в рівняння
. (2.2)
Постійність ΔH й R дозволяє інтегрувати рівняння (2.2) та одержати наступне співвідношення
. (2.3)
Рівняння (2.3) відповідає прямолінійній залежності в координатах lnp - 
. По тангенсу кута нахилу прямої можна визначити теплоту випарування:
.
Звідки ΔН = −8,314 tg α, де α - кут, що утворений прямою й віссю абсциси.
Інтегрування рівняння (2.2) в інтервалі температур від T1 до T2 приводить до виразу
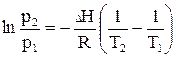, (2.4)
яке дозволяє розрахувати теплоту випарування, знаючи тиск насиченої пари при двох температурах.
З метою підвищення точності при вирішенні рівняння (2.2) треба врахувати температурну залежність теплоти випаровування, скориставшись рівнянням Кірхгофа
, (2.5)
де ΔcР - різниця значень молярної теплоємності конденсованої фази й насиченої пари.
При більше точному рішенні варто враховувати, що й сама величина ΔcР є функцією температури, тому залежність ΔН від T можна виразити рівнянням
ΔН = Δа + ΔbТ + ΔсТ2 + const', (2.6)
де Δа, Δb, Δс - емпіричні коефіцієнти, const' – константа інтегрування рівняння (2.5).
Вносячи ці виправлення, при інтегруванні рівняння (2.2) одержують більш точне рівняння p = f(T). Якщо обмежитися двома членами правої частини рівняння (2.6), то залежність p від Т матиме вигляд
. (2.7)
Слід мати на увазі, що пара може вважатися ідеальним газом при досить низьких значеннях тиску коли між молекулами пари практично не існує сил зчеплення, а об'єм молекул значно малий у порівнянні з об'ємом, що займає пара.
