Геометрические образы правильной формы (многогранники и поверхности вращения – прямой круговой цилиндр, прямой круговой конус, сфера, правильные призмы и пирамиды) часто встречаются в реальных деталях машин и механизмов.
Правильные геометрические тела характеризуется наличием в них различных осей и плоскостей симметрии, что позволяет строить аксонометрические изображения этих тел по принципу симметрии.
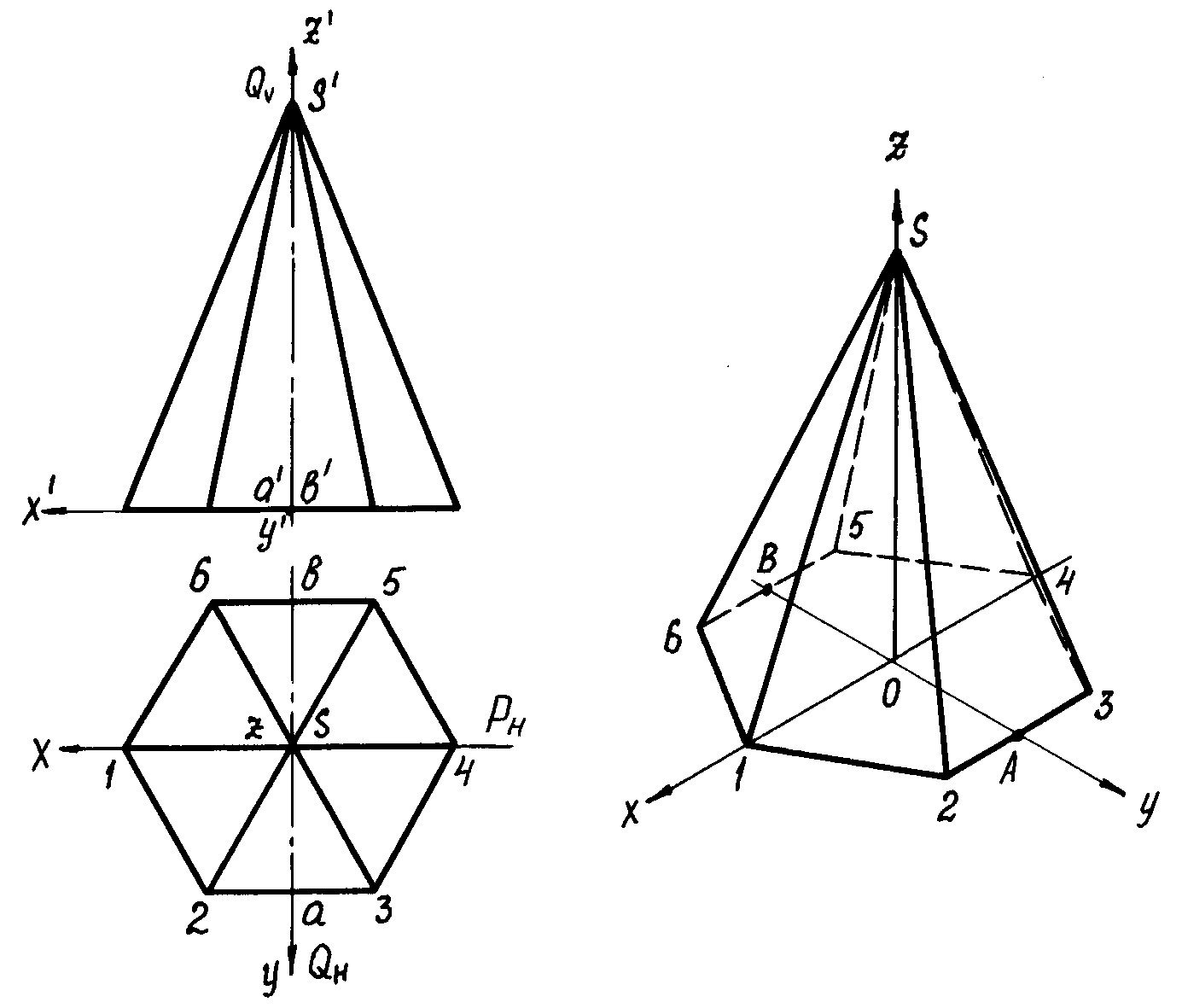Допустим, требуется построить аксонометрическое изображение прямой шестигранной пирамиды (рис.27). Прежде всего отнесем рассматриваемый геометрический образ к системе прямоугольных координат, выбрав положение осей так, чтобы они лежали в соответствующих плоскостях симметрии. При таком положении осей видно, что элементы геометрического образа располагаются симметрично относительно плоскостей Р и Q и, следовательно, относительно осей ОХ и ОУ. Строим аксонометрические оси (например, для ортогональной изометрии) и на этих осях откладываем точки 1, 4 по оси ОХ и a, b по оси ОУ.
Рис. 27. Изображение шестигранной призмы в изометрии
На горизонтальной проекции геометрического образа эти точки располагаются симметрично относительно осей ОХ и ОУ (или относительно начало осей точки О). Следовательно, в аксонометрии они располагаются таким же образом.
Строим стороны основания 23 и 56, которые параллельны оси ОХ, так как их проекции параллельны этой же оси. Найдя аксонометрическое положение вершины S, строим полную аксонометрическую проекцию данного геометрического образа*.
Принцип симметрии используется для построения наглядных изображений любых правильных многогранников.
Построение наглядных изображений правильных поверхностей вращения несколько отлично от рассмотренного, т.к. в основе этих поверхностей лежат окружности, аксонометрические проекции которых изображаются эллипсами.
Пусть требуется построить аксонометрическую проекцию конической втулки, изображенной на рис.28. Отнесем данное тело к декартовой системе осей координат, приняв за начало координат точку 0 в центре правого основания втулки. Построим аксонометрические оси. Аксонометрическую проекцию втулки можно выполнить тремя различными вариантами построений.
Рис. 28. Аксонометрическая проекция втулки
Первый вариант – вначале построить эллипс I, затем эллипс II и, наконец, эллипс III, т.е. построения начинаем с левого (меньшего) основанием втулки.
Второй вариант–вначале строим эллипс III, затем эллипс II и, наконец, эллипс I.
Третий вариант – вначале строим сечения в плоскостях XOZ и XOY, затем пристраиваем к ним внешние контуры детали.
Замечание. Очерковые образующие цилиндрической поверхности втулки всегда проходят через точки В1В2 и А1А2 – т.е. через концы больших осей эллипсов оснований цилиндра.
Что же касается очерковых образующих конической поверхности, то они не проходят через точки ВВ1 и АА1 , а являются касательными к эллипсам оснований усеченного конуса.
Студенты часто допускают ошибки при изображении конической поверхности, проводя очерковые образующие конуса через концы большой оси эллипса основания.
Рассмотренным приемом строятся наглядные изображения всех линейчатых поверхностей вращения. Построение очерковых линий – линий внешнего видимого контура поверхности вращения может быть выполнено 2 способами.
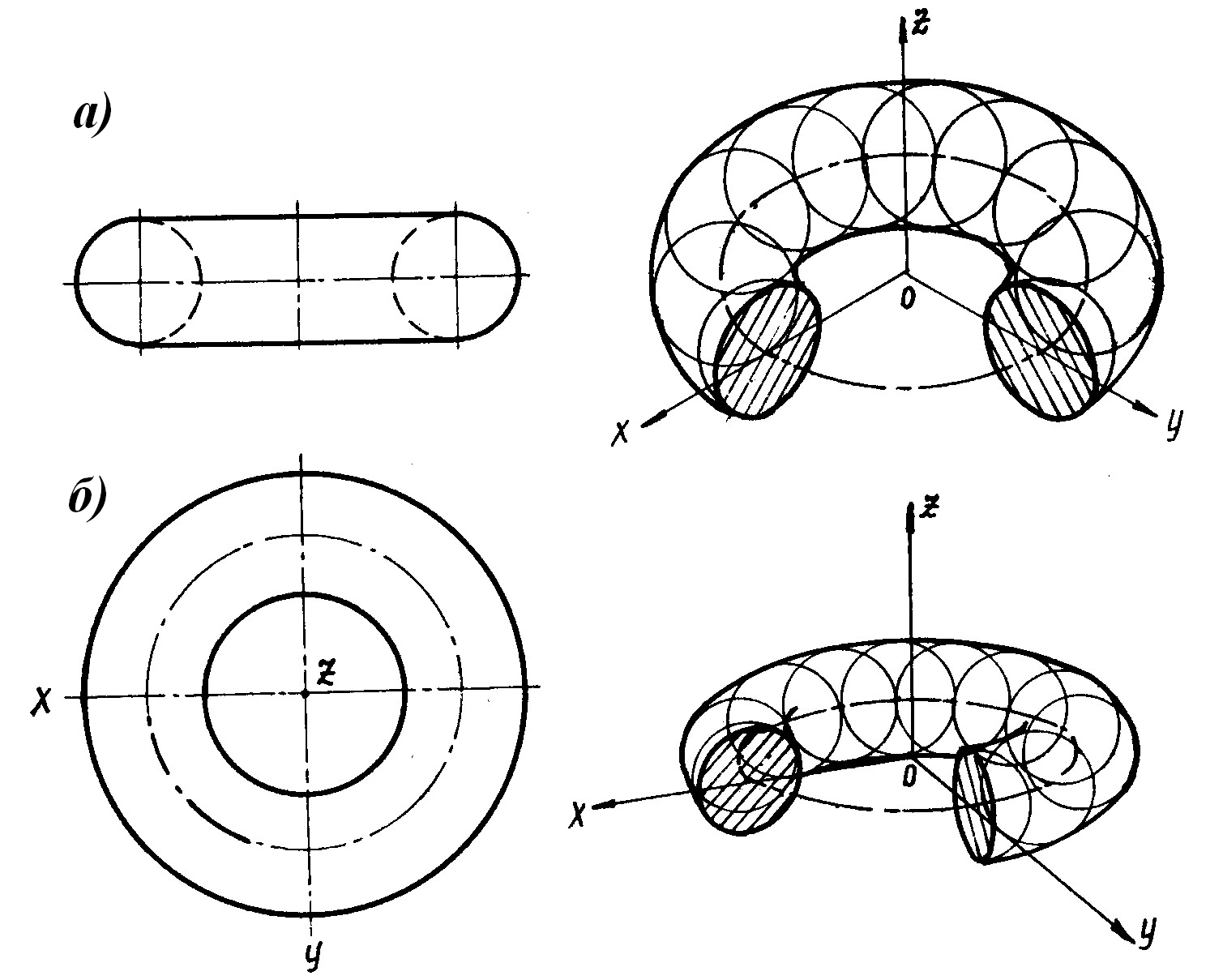
1. Способ плоских сечений – параллелей применяется для некоторых поверхностей вращения (например, вытянутый в направлении оси ОХ параболоид, закрытый тор, эллипсоид и т.д.). На рис.29, а, проведены произвольные секущие плоскости (Q, R, P и т.д.) перпендикулярные оси вращения параболоида, которые пересекают его по параллелям l (l1,l2). В прямоугольной диметрии (рис.29, б) построен ряд эллипсов, соответствующих параллелям, затем огибающая их линия, которая и дает очерк параболоида вращения.
Рис. 29. Способ плоских сечений
Способ вспомогательных шаров применяется для трубчатых поверхностей. Тор можно представить в виде поверхности, обертывающей систему шаров с центрами на осевой линии кольца. Поэтому на рис.30 сначала построена аксонометрическая проекция окружности осевой линии кольца, находящейся в плоскости ХОУ, т.е. эллипс L. Из произвольных точек эллипса построен ряд окружностей заданного диаметра – аксонометрических проекций, вписанных в тор шаров. Линии, огибающие эти окружности, дают искомый очерк аксонометрической проекции кольца, состоящий из двух кривых, эквидистантных эллипсу L. На рис.30,а представлена изометрическая проекция тора, на рис.30, б– диметрическая.
Форма некоторых деталей машин и механизмов представляет собой неправильные геометрические тела, причем они могут быть как многогранниками, так и кривыми поверхностями.
Аксонометрические проекции многогранников неправильной формы, как правило, строятся координатным способом.
Рис. 30. Способ вспомогательных шаров
а – изометрическая проекция тора
б – диметрическа проекция тора
Рассмотрим пример (рис.31). Пусть требуется построить аксонометрическую проекцию изображенного в ортогональных проекциях геометрического образа. Отнесем геометрический образ к декартовой системе осей координат. Поскольку геометрический образ несимметричен, оси можно выбрать произвольно. Отметим опорные точки, в качестве которых можно использовать вершины многогранника 1, 2, …15, 16. Построим аксонометрические оси (в ортогональной изометрии). Для этого определим координаты опорных точек по проекционному чертежу и затем строим аксонометрические проекции этих точек. Полученные точки соединяем соответственно проекционному чертежу.
В рассматриваемом примере построения удобнее вести начиная с нижнего основания, т.е. снизу вверх.
В случае, если некоторые поверхности геометрического образа являются кривыми (рис.32), его аксонометрическая проекция строится с помощью дополнительных сечений S1,S2…..Sn. Эти сечения выполняются, как правило, плоскостями уровня. Порядок построений в этом случае следующий. Прежде всего построим аксонометрические оси и перенесем на аксонометрическое изображение опорные точки ABCD и EFGH. Далее задаем горизонтальные секущие плоскости S1,S2…..Sn, каждая из которых пересекает криволинейный контур геометрического образа по отрезкам 12, 34…… Эти точки координатным способом переносим на наглядное изображение и соединяем соответственно с помощью лекала. Способ дополнительных сечений используется во всех случаях, где непосредственно построения невозможны для передачи формы геометрического образа. Это, прежде всего, относится к изображениям поверхностей топографического характера, к изображениям нелинейчатых поверхностей вращения и поверхностей случайной формы.
Рис. 31. Пример построения геометрического образа в аксонометрии
Рис. 32. Пример построения геометрического образа в аксонометрии
