Чтобы получить наглядное аксонометрическое изображение некоторого геометрического образа, прежде всего, его нужно «привязать» к системе декартовых осей координат, затем выбрать направление проецирования, отличное от направления любой из декартовых осей и параллельно этому направлению спроецировать геометрический образ на картинную плоскость. Полученное таким образом параллельное изображение геометрического образа будет его аксонометрической проекцией. Грани геометрического образа, параллельные плоскостям проекций, в аксонометрической проекции не будут вырождаться в отрезки прямых. Следует отметить, что в общем случае происходят искажения как угловых величин геометрического образа (в том числе и декартовых углов), так и его линейных размеров. Однако эти искажения не мешают объемному восприятию, а, наоборот, ему способствуют. Таким образом, сутью аксонометрических проекций является построение параллельной проекции геометрического образа на плоскость, когда направление проецирования не совпадает ни с одной из декартовых осей координат (рис.1. б, в).
Рис.1. Проекция точки
а)ортогональная проекция точки А б) изометрическая проекция точки А
в) диметрическая проекция точки А
Виды аксонометрических проекций.
Аксонометрические проекции называют прямоугольными если направление проецирования и проецирующие прямые перпендикулярны плоскости, на которую они проецируются, и косоугольными если направление проецирования не перпендикулярно плоскости аксонометрических проекций. Проекции аксонометрических осей на плоскость называют аксонометрическими осями, а проекции единицы измерения по осям – аксонометрическими единицами измерения.
В зависимости от положения предмета и осей координат относительно плоскости проекций, а также в зависимости от направления проецирования единицы измерения проецируются в общем случае с искажением. Искажаются и размеры проецируемых предметов. Отношение длины аксонометрической единицы к ее истинной величине называют показателем или коэффициентом искажения для данной оси координат. Аксонометрические проекции называют изометрическими, если коэффициенты искажения по всем осям равны; диметрическими, если коэффициенты искажения по двум осям равны и триметрическими, если все коэффициенты различны. Для аксонометрических изображений предметов применяют пять видов аксонометрических проекций: прямоугольные – изометрические и диметрические, косоугольные – фронтальные диметрические, фронтальные изометрически и горизонтальные изометрические.
Изометрия
В изометрических проекциях углы между аксонометрическими осями равны между собой и численно определяются как 3600 /3=1200. Коэффициенты искажения также равны между собой. Их численное значение определяется из известного выражения (ф-ла 1), но поскольку k=m=n,
выражение примет вид 3 k2 =2,
отсюда k =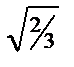 
= 0,82,
т.е. коэффициенты искажения в изометрии равны по 0,82. Это значит, что все линейные размеры геометрического образа, принимаемые параллельно осям декартовой системы координат, в изометрии искажаются в 0,82 раза. На рис.2 показаны ортогональные проекции параллелепипеда, отнесенного к декартовой системе координат. Его линейные размеры соответственно равны а, в и с. В аксонометрической проекции ребра параллелепипеда соответственно равны 0,82 а, 0,82 в и 0,82 с. Чтобы не производить арифметические подсчеты, удобно пользоваться графическим масштабом, теоретическая суть которого основана на теореме Фалеса. Принимаются две пересекающиеся прямые (для удобства примем прямой угол). Одну из прямых ограничиваем десятью единицами измерений, вторую восемью и двумя десятыми, полученные точки соединяем (рис.2). Пользоваться графическим масштабом очень просто: на вертикальной прямой отмечаем натуральный размер геометрического образа и через полученную точку проводим прямую, параллельную отрезку S до пересечения с горизонтальной прямой. Полученный таким образом отрезок равен 0,82 натуральной величины.
Диметрия
В диметрических проекциях два угла между аксонометрическими осями равны по 131°25' и третий угол составляет 97°10', причем ориентация осей может быть левой и правой (рис.3).
Коэффициенты искажения по аксонометрическим осям соответственно равны: два по 0,94 и третий – 0,47. Это значит, что линейные размеры геометрического образа, принимаемые параллельно декартовым осям координат, в диметрии соответственно искажаются в 0,94 и в 0,47 раза.
Практически углы между аксонометрическими осями выдерживаются равными указанным, если через начало координат провести горизонтальную прямую и отложить от нее вниз углы равные 41°25' и 7°10'(рис.3). Приближенно можно принять, что tg 7°≈1/8 и tg 41°≈ 7/8, тогда, чтобы отложить эти углы, нужно выполнить следующие построения: на горизонтальной вспомогательной прямой от начала координат влево и вправо откладываем по 8 единиц и вниз соответственно одну и семь единиц. В первом случае получим угол 7°, во втором - 41°. Следует помнить, что большее искажение всегда происходит по оси, наклоненной к горизонтальной прямой под углом 41°25' (по этой оси коэффициент принимается 0,47, а по двум другим – 0,94). Причем, при левой ориентации аксонометрических осей большее искажение происходит по оси ОХ, при правой ориентации – по оси ОУ.
На рис.3 показаны различные варианты расположения аксонометрических осей в диметрии, а также построение простейшей геометрической фигуры в диметрии. Как и в предыдущем случае, при построении диметрии удобно пользоваться графическими масштабами.
В практике машиностроительного черчения, с целью упрощения и удобства построения, пользуются не истинными коэффициентами искажения в изометрии и диметрии, а так называемыми приведенными коэффициентами. В изометрии вместо коэффициента искажения 0,82 принимают 1, искусственно увеличивая коэффициент искажения в 1: 0,82=1,22 раза, что приводит к увеличению объемного изображения в 1,22 раза.
Аналогично поступают и при построении диметрических проекций. Так, вместо истинных коэффициентов искажения 0,94; 0,94; 0,47 принимают соответственно 1,1 и 0,5. В этом случае увеличение коэффициентов происходит в 1: 0,94=1,06 раза, что также приводит к увеличению объемного изображения в 1,06 раза.
Использование приведенных коэффициентов искажения удобно и значительно упрощает построения. Аксонометрические проекции, построенные по истинным коэффициентам искажения, называются нормальными, изображения же, построенные по приведенным коэффициентам искажения, называются увеличенными или практическими.
Основной задачей аксонометрических проекций является достижение наглядности изображения.
Использование приведенных коэффициентов искажения вполне и проще решает эту задачу. Вот почему аксонометрические проекции, выполняемые по приведенным коэффициентам искажения, столь широко применяются в практике.
Расположение осей и порядок построения в увеличенной аксонометрии остается аналогичным рассмотренным примерам (рис.2, 3). Отличие заключается лишь в том, что в изометрии ребра параллелепипеда в аксонометрии вовсе не искажаются, а в диметрии происходит искажение по одной из осей в 0,5 раза.
Кроме указанных выше ортогональных изометрической и диметрической проекций, применяемых наиболее часто Государственный стандарт предусматривает также применение следующих видов косоугольных аксонометрических проекций:
а) косоугольная фронтальная диметрия
б) косоугольная горизонтальная изометрия
в) косоугольная фронтальная изометрия.
Рис. 2. Прямоугольная изометрия
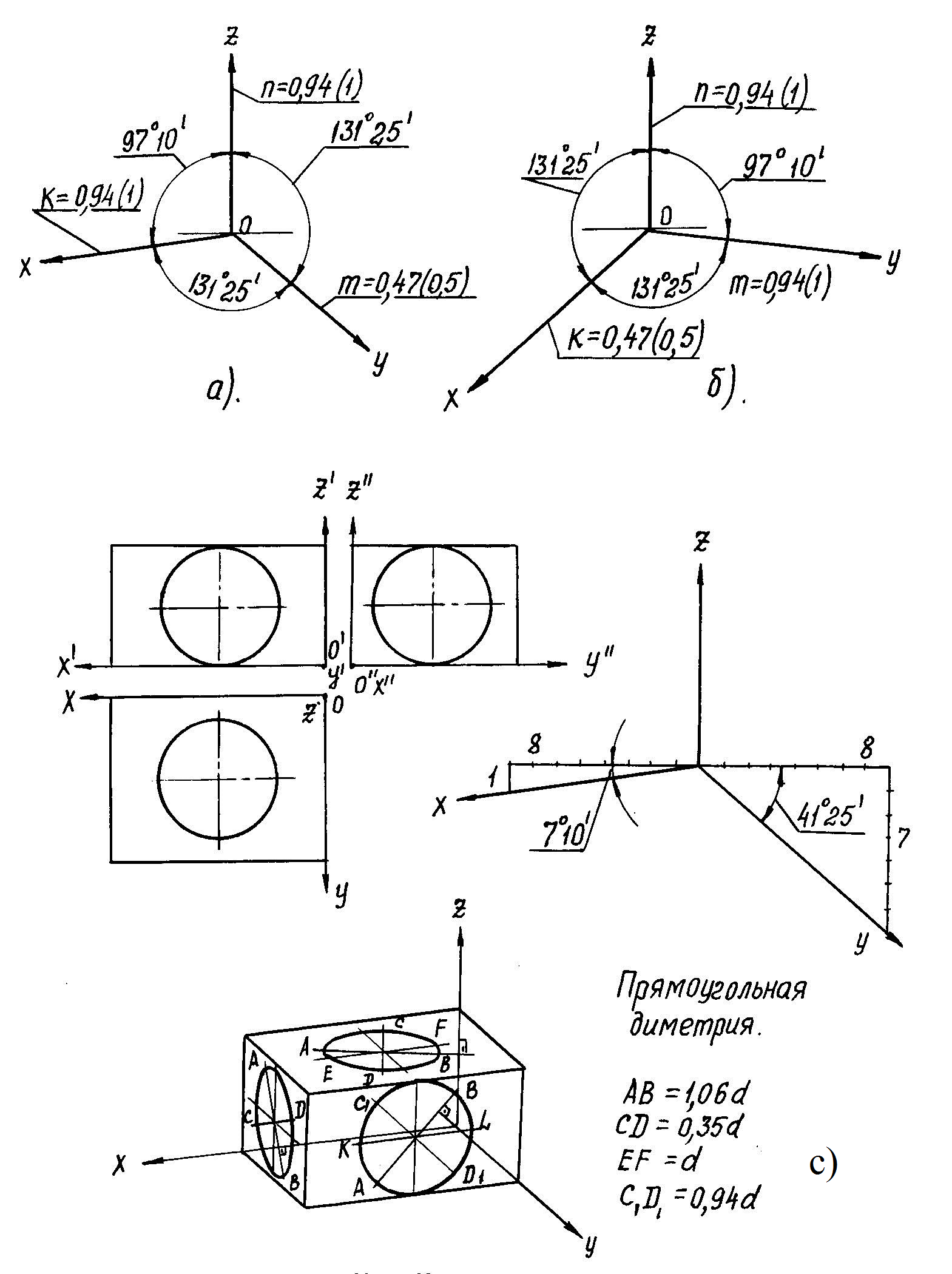
Рис.3. Прямоугольная диметрия
а,б, – варианты расположения аксонометрических осей в диметрии
с – геометрическая фигура в диметрии
ПРЯМОУГОЛЬНЫЕ АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
