Средние величины – это обобщающая количественная характеристика совокупности 1ых явлений по одному какому-либо признаку. Средняя величина характеризует всю массу единиц в выражает то общее, что характерно для данной совокупности в целом. Например по данным о з/п работников предприятия (500 руб.) определяется средняя з/п, которая характеризует всю эту совокупность.
Основные принципы исчисления среднего:
- Качественная однородность совокупности
Средняя з/п по стране средняя з/п по отдельным отраслям средняя з/п на отдельные предприятия средняя з/п отдельных категорий работы предприятий.
- Исчисление средних для массовых данных
- Кроме средних необходимо изучать наибольшее и наименьшее значение признака, чтобы выявить то, что не типично выявить для данной совокупности.
Виды средних величин
Виды средних величин:
1. Среднеарифметическая (простая и взвешенная)
2. Средняя хронологическая
3. Средняя гармоническая
4. Структурные средние (мода и медиана)
· Средняя арифметическая простая
Применяется для исчисления по 1 ряду чисел.
Определяется средняя з/п рабочих за квартал, если:
В январе 8000 руб.
В феврале 9500 руб.
В марте 9300 руб.
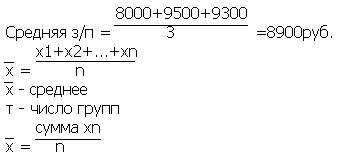
· Средняя арифметическая взвешенная
Применяется, если отдельное значение признака повторяется несколько раз и средняя величина находится по двум рядам чисел. Ряду показателей и ряду весов. Ряд показателей – это ряд чисел, среднее значение которых надо вычислить. Ряд весов показывает сколько раз повторяется каждый показатель.
Исчислить среднюю з/п бригады рабочих, если
3 – 15000
2 – 12500
5 – 17000
Средняя з/п = 3*15000+2*12500+5*17000=155000
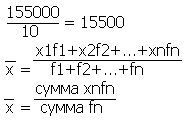
· Средняя гармоническая
Определить среднюю себестоимость продукции, используя следующие данные
| № завода | Издержки производства xifi | Себестоимость единицы продукции (руб.) X1 |

· Средняя хронологическая применяется, когда отдельное значение признака относится к определенному времени.
Определить средний остаток товара на складе за квартал:
На 1 января – 4234,2 тыс. руб.
На 1 февраля – 3898,6 тыс. руб.
На 1 марта – 4126,3 тыс. руб.
На 1 апреля – 4058,3 тыс. руб.

· Средняя геометрическая – применяется для исчисления средних темпов роста и прироста
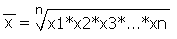
Рост выпуска продукции на предприятии характеризует следующие данные
2001г. по сравнению с 2000г. – 103,8%
2002г. по сравнению с 2001г. – 99,6%
2003г. по сравнению с 2002г. – 101,5%
2004г. по сравнению с 2003г. – 100,7%

· Структурная средняя
В статистике применяются такие средние как мода и медиана (структурные средние)
Мода – это значение признака, чаще всего встречающегося в совокупности.
В секции мужской обуви проданы туфли следующих размеров:
40 размер – 5 пар
41 размер – 8 пар
42 размер – 12 пар
43 размер – 10 пар
44 размер – 6 пар
45 размер – 3 пар
Мода = 42 размер, так как этот размер обладает наибольшей численностью
Медиана – это значение признака в возрастающем или убывающем ряду, который находится в середине ряда.
Рабочие по стажу распределены следующим образом
2, 4, 7, 8, 10 лет
2, 4, 7, 8, 10, 12 лет

Определить медиану по средней з/п рабочих
| Месячная з/п | Число рабочих | Сумма накопленных частот |
| 33 (15+18) 56 (33+23) | ||
| Итого |
Медиана 15000 тыс. руб., так как сумма накопленных частот для этого признака чуть больше половины.
Медиана находит практическое применение вследствие особого свойства: сумма абсолютных отклонений членов ряда от медианы, есть величина наименьшая. Это свойство медианы может быть использовано при проектировании расположения трамвайных остановок, бензоколонок и т.д.






