Вариация (варьирующие признаки) - это изменение значения признака при переходе от одной единицы совокупности к другой. Вариацию можно определить как количественное различие значений одного и того же признака у отдельных единиц совокупности. Изучение вариации в статистической практике позволяет установить зависимость между изменением, которое происходит в исследуемом признаке, и теми факторами, которые вызывают данное изменение.
Для измерения вариации признака используют как абсолютные, так и относительные показатели.
К абсолютным показателям вариации относят: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсию.
К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение и др.
Абсолютные показатели:1.размаха вариации Н как разницы между максимальным (Xmax) и минимальным (Xmin) наблюдаемыми значениями признака:H=Xmax - Xmin.Однако размах вариации показывает лишь крайние значения признака. Повторяемость промежуточных значений здесь не учитывается;2.Более строгими характеристиками являются показатели колеблемости относительно среднего уровня признака. Простейший показатель такого типа – среднее линейное отклонение Л как среднее арифметическое значение абсолютных отклонений признака от его среднего уровня;3.Показатель среднего линейного отклонения нашел широкое применение на практике. С его помощью анализируются, например, состав работающих, ритмичность производства, равномерность поставок материалов, разрабатываются системы материального стимулирования. Но, к сожалению, этот показатель усложняет расчеты вероятностного типа, затрудняет применение методов математической статистики;4. В общей теории статистики показатель дисперсии является оценкой одноименного показателя теории вероятностей и (как сумма квадратов отклонений) оценкой дисперсии в математической статистике, что позволяет использовать положения этих теоретических дисциплин для анализа социально-экономических процессов.
Относительные показатели:1.Коэффициентом осцилляции отражает относительную колеблемость крайних значений признака вокруг средней 
; 2. Относительное линейное отключение характеризует долю усредненного значения признака абсолютных отклонений от средней величины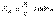 
; 3. Коэффициент вариации: 
является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин.
