Свободные затухающие колебания в контуре с омическим сопротивлением

Всякий реальный колебательный контур обладает активным (омическим, т. е. с пренебрежимо малыми индуктивностью и емкостью) сопротивлением R. В отсутствие внешней ЭДС (ε =О) энергия, запасенная в контуре, постепенно расходуется в этом сопротивлении на его нагревание в соответствии с законом Джоуля-Ленца, вследс­твие чего свободные колебания затухают. Уравнение, описывающее сво­бодные (ε =О) затухающие колебания в контуре с омическим сопро­тивлением R≠ О получается из (3) и имеет вид:

(9)

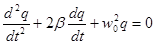
где . Это уравнение совпадает с дифференциальным уравне­нием затухающих механических колебаний. При условии 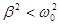, т. е..
_ решение (9) имеет вид:

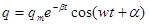(10)

где - частота затухающих колебаний, которая меньше собственной частоты контура w₀ Для напряжения на конденсаторе имеем

,

а продифференцировав q по времени, можно получить выражение для зависимости силы тока от времени, причем оказывается, что при нали­чии активного сопротивления сила тока I опережает по фазе напряже­ние на конденсаторе И более чем на 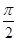. Период колебаний Т равен:

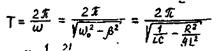(11)

За время ' 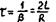амплитуда колебаний уменьшается в е = 2,71..раз. Таким образом, при наличии в контуре активного сопротивления, также имеет место колебательный процесс, однако частота колебаний отличается от частоты свободных колебаний и амплитуда колебаний убывает по экспоненциальному закону. График изменения заряда со вре­менем в этом случае изображен на рис. 2. Графики для напряжения и

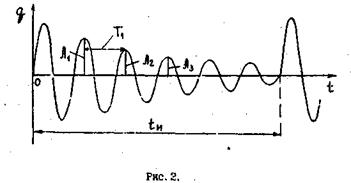
силы тока имеют аналогичный вид. Следует отметить, что решение (10) не является строго периодической функцией, т, к. q(t)≠q(t+T) Говорить о периоде этой функции можно лишь в том смысле, что она принимает нулевые значения через равные промежутки времени. Быстро­та убывания амплитуды колебаний определяется параметром β, харак­теризующим соотношение активного сопротивления контура и его индук­тивности. На практике, же обычно пользуются другими понятиями, связанными с β логарифмическим декрементом затухания λ и добротностью контура Q.

Логарифмическим декрементом затухания называют натуральный ло­гарифм отношения величины заряда при n-ом колебании к величине q-при n+1- ом колебания:

(12)

Логарифмический декремент затухания связан с числом полных коле­баний N, совершаемых pа время Т, зависимостью:

Добротность контура Q определяется через логарифмический декре­мент затухания Λ следующим образом:

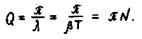(13)

Иэ данных определений видно, что чем меньше логарифмический декремент затухания, тем выше добротность контура и тем дольше продолжается в таком контуре -колебательный процесс при однократном его возбуждении. При выполнении условия w₀²-β²=0 решение (9) для заряда q имеет вид

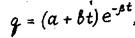(14)

где а.b- постоянные интегрирования. При любых a и b (см. рис. 3)

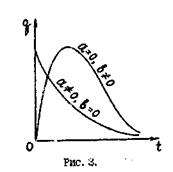величина q- асимптотически приближается к нулю, когда t→∞. В этом случае про­цесс не будет колебательным, т. в. являет­ся апериодическим (рис, 3). Сопротивле­ние R.*p,при котором колебательный про­цесс в контуре переходит в апериодичес­кий, называется критическим и определяет­ся из условия w₀²-β²=0, откуда При R>R_kp, w₀²<β² апериодический характер процессов в колебательном конту ре сохраняется.