Свободные колебания в контуре без омического сопротивления

Свободные колебания, которые имеют место при отсутствии внешней ЭДС., в идеальном контуре без

(4)

омического сопротивления при R. -О, описываются уравнением, следующим из (3) при R - О:

где введено обозначение . Пусть в начальный момент времени t = О конденсатор заряжён до некоторой разности потенциалов U_m (при заряде на пластинах q_m),а ток в цепи отсутствует. Далee емкость начинает разряжаться и в контуре начинает течь ток. Энергия электрического поля в конденсаторе начинает уменьшаться, но возникает всё возрастающая энергия магнитного поля, обусловленного током, текущим через индуктивность. В момент, когда напряжение на конденсаторе и энергия электрического поля обращаются в ноль, ток и энергия магнитного поля достигают наибольшего значения. Начиная о этого момента ток уменьшается и течет за счет ЭДС самоиндук­ции. Когда заряды на обкладках конденсатора достигнут первоначаль­ного значения q_m, но с противоположными знаками, сила тока ста­нет равной нулю. Затем те же процессы протекают в обратном направ­лении, после чего система приходит в исходное состояние и весь цикл повторяется снова и снова, представляя собой электрические колебания.

Решением уравнения (4) является функция

(5)

В этом можно убедиться путем подстановки ее в уравнение (4). Отсю­да следует, что введенная нами величина w₀ представляет собой собственную круговую (циклическую) частоту колебаний. Соответс­твенно для U и I получаем:

(6)

где - максимальные значения напряжения и тока, α - начальная фаза колебаний. Таким образом, заряд на обкладках конденсатора изменяется по гармоническому закону с частотой w₀. Для периода колебаний Т,по истечении которого зна­чения изменяющейся величины периодически повторяются, т. е W₀t=2π (см. (6)),· получаем формулу Томсона:

(7)

При этом частота колебаний . Сила тока опережа­ет по фазe напряжение и заряд на конденсаторе на 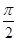,т.е. в момент времени, когда ток достигает наибольшего значения, заряд и напряже­ние на конденсаторе обращаются в нуль, и наоборот. Когда конденсатор заряжен до максимальной разности потенциалов , в
его электрическом поле содержится энергия , а ток отсутствует. В момент времени, когда разность потенциалов и энергия эле­ктрического поля между обкладками конденсатора равны нулю, ток в контуре максимален и в магнитном поле катушки индуктивности запасе­на энергия . Колебания в контуре сопровождаются взаимными превращениями энергий электрического и магнитного полей, при этой в идеальном контуре выполняется закон сохранения энергии:

(8)

и процесс электрических колебаний продолжался бы бесконечно. Под волновым сопротивлением ρ контура понимают индуктивное X_L и ёмкостное Χς сопротивления контура току свободных колебаний, которые равны между собой: