| Связь разности потенциалов с напряженностью для случая одной переменной х или r. |
Точечный заряд.
Подставим в формулу в выражение для напряженности поля точечного заряда. 1 и 2 – любые две точки на радиальной оси координат r. Примем j 1 = 0 при r1 ®¥, заменим j 2 ® j, r2 ® r получим j (r).
| 
|
 (при j¥ = 0)
|
Тема 3. Вопрос 2.
Потенциалы полей различных заряженных тел.
2).Сфера радиуса R, заряженная с поверхностной плотностью заряда s (Кл/м2).
Полный заряд на сфере q = s×4p×R2 . Будем рассматривать две области:1) 
- выбираем две любые точки 1 и 2 в этой области и 2) 
также выбираем две любые точки уже в этой области. Потенциал должен быть непрерывной функцией, в отличие от напряженности он не может иметь разрывов в данной точке, т.к. по смыслу j - потенциальная энергия единичного положительного заряда, а двух энергий у одного заряда в одной точке данного поля не может быть.
|
| Подставим в Напряженность поля сферы. Для получается та же формула, что и для поля точечного заряда.
|
 (при j¥ = 0)
| 
|
 
| |
|
Тема 3. Вопрос 3.
Потенциалы полей различных заряженных тел.
3)Бесконечно длинная нить, заряженная с линейной плотностью заряда t.
Выберем на оси радиальных координат r две любые точки с координатами r1 и r2.
(см. рис.). Подставим в напряженность поля длинной нити и проинтегрируем.
| В этом случае принять j = 0 на бесконечности нельзя (см. график
ln x), поэтому выбираем j = 0 в некоторой произвольной точке с координатой ro. Т.е. примем
 j 1 = 0 при r1 = r0,
заменим j 2 ® j, r2 ® r получим
j (r)
| |
j = 0 при r = r0
| 
| |
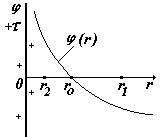
Тема 3. Вопрос 4.
Потенциалы полей различных заряженных тел.
4)Бесконечно протяженная плоскость, равномерно заряженная с поверхностной плотностью заряда s (Кл/м2). Выберем на оси координат х две произвольные точки х1 и х2 .). Используем формулу связи Е и j, подставим выражение для напряженности поля бесконечной плоскости.
| Чтобы получить выражение для потенциала примем 1) j 1 = 0 при х1 = 0 и 2) j 1 = 0 при х1 = d (d – произвольная точка на оси х) |
1)  j = 0 при х = 0
2)  j = 0 при х = d
| 
|
Тема 4. Вопрос 1.
Распределение зарядов в проводниках.
Проводники - есть свободные заряды, которые могут перемещаться по проводнику. Всецелом незаряженный проводник нейтрален. Внесем незаряженный проводник во внешнее Эл. Поле. На заряды внутри проводника действуют силы, которые их перераспределяют. Смещение зарядов будет
Происходить до тех пор, пока результирующее поле внутри проводника не станет равным 0. Только в этом Случае заряды будут находится в равновесии.
- во всем объеме проводника.
Найдем Е поля вблизи поверхности проводника.
Поле только вне проводника, поэтому:
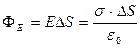
- напряженность вблизи поверхности проводника
Тема 4. Вопрос 2.
