Для любого 
и для любого натурального n имеет место соотношение
а также соотношение
Для доказательства этих соотношений следует применить правило Лопиталя достаточно количество раз. Эти соотношения обобщаются на случай, когда 
-- любое действительное число.
Пример. 
Формула Тейлора
Ставится задача приблизить (аппроксимировать) функцию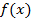 
в окрестности точки 
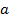многочленом степени n. Для n=1 мы уже нашли решение: 
. Удобно точкой отсчета считать нулевую точку, т.е. от координат 
мы переходим к приращениям 
и 
. Ряд
представляется из себя семейство бесконечно малых величин, каждая последующая из которых есть б.м. большего порядка, чем предыдущая. Поставим задачу о разложении вида
где остаточный член 
есть б.м. высшего порядка по сравнению с 
. Деля (1) на 
и устремляя 
получаем 
. Найдем другие коэффициенты в этом разложении:
Локальная формула Тейлора. Пусть функция 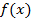дифференцируема в окрестности точки 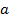n раз, и n-ая производная непрерывна в точке 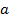. Тогда
Доказательство. Применяем n раз правило Лопиталя к вычислению предела отношения
и доказываем, что этот предел равен 0.□
В условиях теоремы функция 
раскладывается в окрестности точки a в сумму многочлена степени ≤ n от переменной 
и остаточного члена 
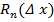, про который известно, что он есть величина бесконечно малая высшего порядка по сравнению с 
.
Функция 
линейна по переменной , она называется дифференциалом 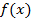в точке 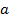и обозначается 
Легко видеть, что 
. Мы получаем «симметричный» вид дифференциала вычисленный в произвольной точке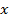 
:
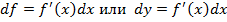
Отсюда получаем, что производная равна отношению дифференциалов: 
Аналогично, функция 
называется дифференциалом -го порядка и обозначается 
. Ее симметричный вид есть 
. Тогда локальная формула Тейлора в дифференциалах принимает вид:
Уточним вид остаточного члена
Формула Тейлора с остаточным членом в форме Лагранжа. Пусть функция дифференцируема в окрестности точки 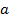n+1 раз. Тогда для всех 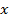достаточно близких к 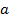найдется точка 
такая, что
В частности, если 
, то имеет место следующая оценка остаточного члена:
Частный случай формулы Тейлора -- формула Маклорена получается при 
. Тогда при наличии n+1 производной в окрестности нуля, для каждого достаточно малого 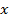найдется 
такой, что
Разложение элементарных функций по формуле Маклорена
Разложение экспоненты
Для всех x∈ ℝ имеет место разложение
где 
Например, если 
, то
Тем самым 
c точностью 
Разложение синуса и косинуса
Для всех 
имеет место разложение
где
Для всех имеет место разложение
где
Бином Ньютона
Для каждого действительного числа α и для каждого 
определим биномиальный коэффициент
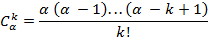
По определению полагаем также, что 
. Имеем:
Теорема. Для любого действительного α и для любого 
имеет место разложение
причем
Рассмотрим частные случаи формулы (5).
Случай α =m -- натуральное число. Тогда 
и мы получаем бином Ньютона
Случай 
. Тогда нетрудно вывести, что 
. Поэтому
где
Разложение логарифма
Из (8) или непосредственно нетрудно получить
где
