Применение средних величин в анализе хозяйственной деятельности

ОАО «Татнефть»

В данной части курсовой работы будут приведены статистические данные о деятельности подразделений ОАО «Татнефть», одной крупнейших нефтедобывающих компаний в России, рассчитаны средние показатели по этим данным, а также сделаны анализ и выводы по полученным результатам.

Приведем следующие данные:

Таблица 3

Показатели работы буровых бригад

Год	Проходка на долото, м	Механическая скорость бурения,
	149,5 156,4 146,2 146,9 143,3 142,6	11,3 10,4 9,6 9,6 10,2 9,4

 

Источник: Гиниатулин М.К., «Развитие «Татнефти»», Москва, 2000, с.33.

Зная проходку на долото и механическую скорость бурения, рассчитаем среднюю скорость, используя формулу средней гармонической взвешенной.

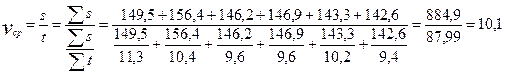
Т.е. средняя механическая скорость бурения составляет 10,1 за период с 1993 по 1998 год.

Далее приведем данные об объеме подготовки нефти в ОАО «Транснефть» и рассчитаем среднее значение с помощью формулы средней арифметической: .

Таблица 4

Объем подготовки нефти

(тыс. тонн)

Год	Общий объем подготовленной нефти
	32330,6 28803,8 24685,9 22361,0 23375,9 23218,4 22297,0 23900,0

 

Источник: Гиниатулин М.К., «Развитие «Татнефти»», Москва, 2000, с.81.

тыс.т

Т.о. среднее значение объема подготовки нефти за период с 1991 по 1998 год составляет 25121,6 тыс.тонн.

Используя данные таблицы 4, рассчитаем средний темп роста по формуле средней геометрической:

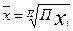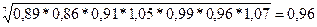= или 96%

Далее, используя формулу средней арифметической взвешенной ()и данные по предприятию, рассчитаем среднюю выработку продукции в объединении «Татнефть» за 1991 по 1997 год.

Таблица 5

Среднесписочная численность и производительность труда

Год	Среднесписочная численность работников	Средняя выработка на 1 работника, тонн/чел.

 

Источник: Гиниатулин М.К., «Развитие «Татнефти»», Москва, 2000, с.143.

 

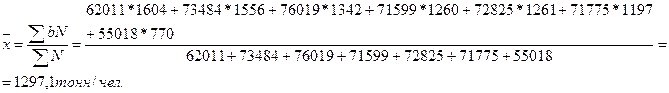Следовательно, выработка продукции на 1 человека в среднем за семь лет составляет 1297, 1 тонн/чел.

Следующий расчет связан с определением средней заработной платы работников за период с 1991 по 1998 год по следующим данным:

 

Таблица 6

Среднесписочная численность и среднемесячная зарплата (с учетом выплат из ФМП) промышленно – производственного персонала в нефтедобыче

Год	Численность, чел.	Средняя зарплата одного работника, руб.

 

Источник: Гиниатулин М.К., «Развитие «Татнефти»», Москва, 2000, с.145.

Здесь также применим формулу средней арифметической взвешенной.

Далее рассмотрим основные показатели работы объединения «Татнефть» в Тюменской области. По данным показателей работы буровых бригад рассчитаем среднюю проходку на бригаду:

Таблица 7

Показатели работы буровых бригад Тюменской области

Год	Среднегодовое число буровых бригад	Проходка на бригаду,м
	41,5 36,8 30,6 21,7

 

Источник: Гиниатулин М.К., «Развитие «Татнефти»», Москва, 2000, с.196.

 

Средняя проходка на бригаду в год равна:

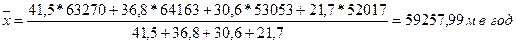
Используя следующие данные по бугульминскому механическому заводу ОАО «Татнефть», определим среднегодовую стоимость основных производственных фондов.

Таблица 8

Стоимость основных производственных фондов

(тыс.руб.)

Год	Стоимость основных производственных фондов

 

Источник: Гиниатулин М.К., «Развитие «Татнефти»», Москва, 2000, с.370.

1. Для определения среднегодовой стоимости основных производственных фондов воспользуемся формулой средней арифметической простой 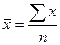(т.к. имеются индивидуальные несгруппированные значения признака, где x₁,x₂,…x_n - среднегодовая стоимость основных производственных фондов; n –число лет).

 

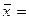
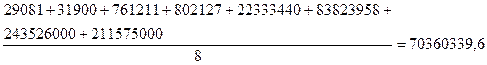тыс.руб.

Среднегодовая стоимость основных производственных фондов равна 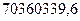тыс.руб.

Далее построим статистический ряд распределения по стоимости основных производственных фондов, образовав 3 группы.

Для этого найдем величину равного интервала. Величина равного интервала определяется по формуле:

 

,

где x_max и x_min – максимальное и минимальное значение признака, n – число групп.

 

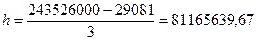
Путем прибавления величины интервала к минимальному значению признака в группе получим следующие группы по значению стоимости основных производственных фондов:

 

Таблица 9

Ряд распределения предприятий по стоимости основных производственных фондов

Интервалы стоимости основных производственных фондов, тыс.руб.	Количество лет	Удельный вес	Центр интервала
29081- 81194720,67 81194720,67 – 162333360,3 162333360,3 - 243499000		0,625   0,125   0,250	40611900,84   121764040,5   202916180,2
Итого		1,000	*

 

а) По ряду распределения рассчитаем среднегодовую стоимость основных производственных фондов, взвешивая варианты признака по числу лет.

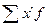, где - сумма произведений среднегодовой стоимости основных производственных фондов предприятий на их количество, 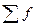- общее число лет.

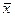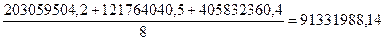= тыс.руб.

Среднегодовая стоимость основных производственных фондов, взвешивая варианты признака по числу лет равна 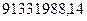тыс.руб.

б) По ряду распределения рассчитаем среднегодовую стоимость основных производственных фондов, взвешивая варианты признака по удельному весу.

Воспользуемся формулой средней арифметической взвешенной, в качестве весов используем относительную величину (d) (удельный вес):

; где - сумма произведений среднегодовой стоимости основных производственных фондов предприятий на их удельный вес, 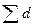=1.

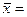40611900,84*0,625+121764040,5*0,125+202916180,2*0,25= 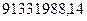тыс.руб.

Среднегодовая стоимость основных производственных фондов, взвешивая варианты признака по удельному весу лет равна 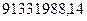тыс.руб.

При сравнении полученных результатов средней обнаруживаем небольшое расхождение, которое объясняется тем, что в первом случае расчет проводился по формуле средней арифметической простой в расчете на один год, во втором случае по формуле средней арифметической взвешенной по ряду распределения по среднегодовой стоимости основных производственных фондов с выделением трех интервалов. Для вычислений мы использовали средние значения в интервале (простая средняя между верхней и нижней границами каждого интервала). При таком исчислении средней допускается некоторая неточность, поскольку делается предположение о равномерности распределения единиц признака внутри группы.

Рассмотрим далее численность выпускников центра подготовки кадров (школы буровых мастеров) в г. Альметьевске и рассчитаем значения моды и медианы.

Таблица 10

Численность выпускников центра подготовки кадров

(человек)

Год	Количество

Источник: Гиниатулин М.К., «Развитие «Татнефти»», Москва, 2000, с.387.

Проведем группировку статистических данных:

Таблица 14

Группировка данных по численности человек

Интервалы численности	Число лет
1520-1984,5 1984,5-2449 2449-2913,5 2913,5-3378
Итого

 

h= 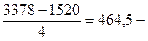величина интервала

Модальный интервал -1520-1984,5 (наибольшая частота, равна 7).

,

где - нижняя граница модального интервала,

- частота модального интервала,

- частота предмодального интервала,

- частота послемодального интервала,

d – величина модального интервала.

 

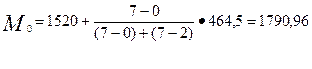
Следовательно, согласно расчетам мода 1790,96 чел.

Рассчитаем медиану, используя формулу:

,

где - верхняя граница предмедианного интервала;

- частота медианного интервала;

d- величина медианного интервала;

- сумма накопленных частот в интервале, предшествующем медианному.

 

.

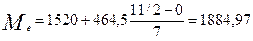Т.о. медиана равна 1884,97 человек.

Соотношение медианы, моды, а также средней арифметической указывает направление и степень ассиметрии распределения. Если мода меньше медианы, то имеет место правосторонняя ассиметрия. Если же медиана меньше моды, то говорят о левосторонней ассиметрии. В нашем случае имеет место правосторонняя ассиметрия распределения численности людей.

 

 

Выводы и предложения

Подводя итоги, следует еще раз подчеркнуть, что средние величины являются обобщающими характеристиками изучаемого признака в исследуемой совокупности. Они отражают типичный уровень в расчете на единицу совокупности в конкретных условиях места и времени.

Важнейшим свойством средней является то, что она через характеристику единицы совокупности характеризует всю совокупность в целом.

Средняя величина применяется:

- для оценки достигнутого уровня изучаемого показателя;

- при анализе и планировании производственно хозяйственной деятельности предприятий, фирм, банков и других хозяйственных единиц;

- при выявлении взаимосвязи между явлениями;

- при расчете нормативов и прогнозирования.

После проведения расчетов по показателям деятельности объединения «Татнефть» необходимо отметить, что можно вычислить следующие величины:

1. Средняя трудоемкость изготовления изделия одного и того же вида несколькими рабочими.

2. Средний уровень выработки продукции в единицу рабочего времени.

3. Средний уровень оплаты труда.

4. Средний уровень фондоотдачи.

5. Средний уровень затрат на производство единицы продукции одного и того же вида на нескольких предприятиях.

В целом, средняя величина играет очень большую роль в статистике. Существует большое количество форм средних. Поэтому важно понять, в каких случаях какой вид средней применяется. Перед решением статистической задачи необходимо усвоить сущность средней величины, являющейся, обобщающей характеристикой одноименных явлений по изучаемому признаку и основные принципы ее вычисления. Нужно понимать то, что средняя должна вычисляться с учетом экономического содержания определяемого показателя.

 

 

Список используемой литературы

1.Гигиадулин М.К.,«Развитие «Татнефти»», Москва, Радиософт,2000г

2.Годин. А.М.,«Статистика», Москва, 2002г

3. Гришин А.Ф., «Статистика», Москва, 2003г

4. Диденко Т.В., Л.В.Колядов, П.Ф. Тарасенко,«Статистика»,

Москва, изд. «Нефть и газ, 2007г

5. Калинина В.П., Диденко Т.В., «Статистика нефтяной и газовой промышленности», Москва, 1983

[1] Годин А.М., «Статистика», Москва, 2002г, с.90-91

[2] Диденко Т.В., Л.В.Колядов, П.Ф.Трасенко, «Статистика», Москва, 2007, с.55

[3] Диденко Т.В., Л.В.Колядов, П.Ф.Трасенко, «Статистика», Москва, 2007, с.56

[4] Гришин А.Ф. «Статистика»,Москва, 2003, с.75 - 76

[5] Годин А.М.,«Статистика», Москва, 2002, с.97-99

[6] Диденко Т.В., Л.В.Колядов, П.Ф.Трасенко, «Статистика», Москва, 2007, с.5

[7] Диденко Т.В., Л.В.Колядов, П.Ф.Трасенко, «Статистика», Москва, 2007, с.59

[8] Диденко Т.В., Л.В.Колядов, П.Ф.Трасенко, «Статистика», Москва, 2007, с.59-61

[9] Годин А.М.,«Статистика», Москва, 2002, с.107

[10] Годин А.М.,«Статистика», Москва, 2002, с.108