Средние величины являются наиболее распространенной формой статистических показателей, используемой в социально – экономических исследованиях. Средняя дают обобщенную характеристику, и ее можно во многих случаях определить через исходное соотношение средней (ИСС) или ее логическую формулу:
ИСС =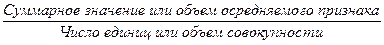 
В статистике выделяют несколько видов средних величин:
1. По наличию признака - веса:
а) невзвешенная средняя величина;
б) взвешенная средняя величина.
2. По форме расчета:
а) средняя арифметическая величина;
б) средняя гармоническая величина;
в) средняя геометрическая величина;
г) средняя квадратическая, кубическая и т.д. величины.
3. По охвату совокупности:
а) групповая средняя величина;
б) общая средняя величина.
Средние величины различаются в зависимости от учета признаков, влияющих на осредняемую величину:
Если средняя величина рассчитывается для признака, без учета влияния на него каких-либо других признаков, то такая средняя величина называется средней невзвешенной или простой средней.
Если имеются сведения о влиянии на осредняемый признак некоторого признака или нескольких признаков, которые необходимо учесть при расчете для корректного расчета средней величины, то рассчитывается средняя взвешенная.
Средние, которые применяются в статистике, относятся к классу степенных, общая форма которых имеет вид[2]:
В зависимости от значения m определяется вид средней:
m=1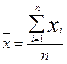 
- средняя арифметическая
m=2 
- средняя квадратическая
m=3 
- средняя кубическая
m=-1 
-средняя гармоническая
m=0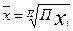 
- средняя геометрическая
Следует отметить, что вид средней зависит от цели исследования и исходной информации.
- правило мажорантности. Это соотношение будет сохраняться при любых значениях признаков.
Средняя арифметическая
Средняя арифметическая является самым распространенным видом средней. Поэтому, когда речь идет о средней величине и не указывается ее вид, то чаще всего подразумевается именно средняя арифметическая. Она применяется, когда объем варьирующего признака для всей совокупности образуется как сумма значений признака у отдельных единиц. Она может быть простой и взвешенной.
Простая средняя арифметическая. Простой средней арифметической называется сумма данных величин, деленная на их число.
Если даны величины 
то их средняя арифметическая есть[3]:
.
Простая средняя арифметическая применяется тогда, когда каждое явление, характеризующее индивидуальное значение варьирующего признака, встречается в совокупности один раз, т.е. не повторяется или повторяется одинаковое число раз. Простая средняя применяется для сгруппированных данных.
Приведем пример. В зависимости от условий и качества работы месячная заработная плата аппаратчиков колеблется от 12 до 16 тысяч рублей и принимает следующие размеры: 12000, 13000, 14000, 15000 и 16000 рублей.
В этом примере данные о значении признака встречаются один раз, и поэтому средний размер заработной платы следует рассчитывать по формуле средней арифметической простой.
= 
Средняя арифметическая взвешенная применяется тогда, когда каждое значение варьирующего признака встречается в совокупности по несколько раз. При этом используются веса или частота признака f:
В целом, использование частот в работе с большими числами позволяет упрощать расчеты, когда частота выражена большими, многозначными числами.
Далее перечислим свойства средней арифметической [4]:
1. Средняя постоянной величины равна ей самой 
2. Произведение средней на сумму частот равно сумме произведений вариантов на частоты: 
3. Изменение каждого варианта на одну и ту же величину изменяет среднюю на ту же величину:
4. Изменение каждого варианта в одно и то же число раз изменяет среднюю в столько же раз:
5. Изменение каждого из весов в одно и то же число раз не изменяет величины средней:
6. Алгебраическая сумма отклонений всех вариантов от средней равна нулю:
7. Средняя суммы равна сумме средних:
8. Сумма квадратов отклонений вариантов от средней арифметической меньше, чем от любых других величин:
Существует также упрощенный способ расчета арифметической (способ моментов). Среднюю арифметическую можно рассчитать следующим образом, используя ее свойства:
1. Вычесть из всех вариант постоянное число (середина ряда, любое значение варианты)
2. Разделить полученные разности на постоянное число (величину интервала)
3. Частоты выразить в долях
4. Применить способ отсчета от условного начала (момента)
m – момент первого порядка
- начало отсчета
d – величина интервала
k – величина интервала всего ряда
Средняя хронологическая
Другим видом средней является средняя хронологическая. Средняя
хронологическая представляет собой средний уровень ряда динамики, т.е. средняя, исчисленная по совокупности значений показателя в разные моменты или периоды времени[5]. В зависимости от вида ряда динамики применяются различные способы ее расчета, а именно расчет: средней хронологической интервального ряда; средней хронологической моментного ряда.
Средней хронологической интервального ряда является средняя величина из уровней интервального ряда динамики. Она исчисляется по формуле:
,
где 
-средний уровень ряда;
y – уровень ряда динамики;
n – число членов ряда.
Средней хронологической моментного ряда является средняя величина из уровней моментного ряда динамики. Если f(t) есть функция, выражающая изменение моментного показателя во времени, то за время t от a до b средняя хронологическая моментного ряда равна:
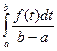
Однако данных непрерывного наблюдения значения f(t) в распоряжении статистики, как правило, нет. Поэтому в зависимости от характера изменения показателя и имеющихся данных применяются различные методы расчета. При равных промежутках времени между датами, на которые имеются данные, и равномерном изменении размера показателя между датами средняя хронологическая моментного ряда обычно исчисляется оп формуле:
,
где y – уровень ряда;
n – число всех членов ряда;
- средний уровень.
Если периоды времени, отделяющие одну дату от другой, не равны между собой, то расчет средней хронологической моментного ряда производится по формуле средней взвешенной арифметической, в качестве весов которой принимаются отрезки времени между датами, т.е по формуле:
,
где Т – время, в течение которого данный уровень ряда остается без изменения.
Средняя гармоническая
Средняя гармоническая применяется в тех случаях, когда имеются общие веса и индивидуальные значения признаков. Она рассчитывается, частоты не приводятся непосредственно, а входят сомножителями в один из имеющихся показателей. Средняя гармоническая – это величина, обратная средней арифметической из обратных значений признаков. Применяется простая и взвешенная.
Простая:
Используется в том случае, когда значения общего веса для единиц совокупности равны.
Взвешенная[6]:
,
где 
- значения общего веса для единиц совокупности.
В качестве весов принимают не единицы совокупности, носительницы признака, а произведения этих единиц на значения признаков.
Например, имеются данные о плановом и фактическом объеме добычи нефти в отдельных ПО Поволжья (см. табл. 3).
Таблица 1
Добыча нефти
(тыс.т)
| ПО | План | Фактическое выполнение | Выполнение плана, % |
| Татнефть Башнефть Куйбышевнефть | 100,1 |
Источник: В.П.Калинина, Т.В. Диденко «Статистика нефтяной и газовой промышленности», часть I, Москва, 1983, с.29
Для вычисления средней гармонической нужно:
1) веса разделить на соответствующие варианты;
2) суммировать веса;
3)суммировать частные от деления весов на варианты;
4) сумму весов разделить на сумму частных от деления весов на варианты.
В вышеприведенном примере степень выполнения плана будет рассчитана следующим образом:
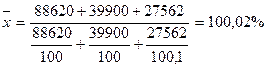
Средняя геометрическая
Средняя геометрическая рассчитывается также по формуле простой и взвешенной[7].
Простая:
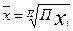
Взвешенная:
Средняя арифметическая взвешенная получила наиболее широкое примение при анализе рядов динамики для расчета среднего темпа роста.
Средняя квадратическая
Для средней квадратической существуют формулы постой и взвешенной:
- простая;
-взвешенная.
Наиболее широко эту среднюю применяют при анализе вариационного ряда для расчета дисперсии и коэффициента вариации.
В статистике находят применение степенные средние и более высокого порядка.
Структурные средние
В статистике употребляется еще две разновидности средних величин, которые вытекают из характеристики статистических рядов и не являются результатом каких – либо алгебраических действий – это структурные средние: мода и медиана. При условии недостаточности исходных данных, которая в ряде случаев объективно может возникнуть при сборе информации (например, коммерческая тайна), предпочтение отдается структурным, или позиционным средним – моде или медиане.
Модой называют значение признака, которой наиболее часто встречается в данной совокупности. Т.е. это величина признака с наибольшей частотой или частостью.
Существуют случаи, когда два и даже более значений признака повторяются одинаково максимальное число раз. В этом случае имеют дело с бимодальным распределением признака и его мультимодальным его распределением. Наличие двух и более модальных значений может означать неоднородность исследуемой совокупности.
При отсутствии повторяющихся значений признака в совокупности первичных данных для определения моды необходимо предварительно выполнить группировку, в результате чего получить интервальный ряд распределения.
Тогда мода определяется по формуле[8]:
,
где - нижняя граница модального интервала,
- частота модального интервала,
- частота предмодального интервала,
- частота послемодального интервала,
d – величина модального интервала.
Модальным называется интервал, которому соответствует наибольшая частота.
Итак, приведем пример расчета моды из интервального ряда на основании данных проходки на долото.
Таблица 2
Проходка на долото
| Проходка на долото,м | Число долот | Кумулятивная частота |
| 0,5 – 3,0 3,0 – 5,5 5,5 – 8,0 8,0 – 10,5 10,5 – 13,0 | ||
| Итого | * |
Источник: В.П.Калинина, Т.В. Диденко «Статистика нефтяной и газовой промышленности», часть I, Москва, 1983, с.46
Для нахождения моды, в первую очередь, нужно определить модальный интервал. Модальным будет интервал, которому соответствует наибольшая частота. В данном примере наибольшей частотой обладает(42) обладает интервал (3,0 – 5,5), где значение варианты лежит в пределах от 3,0 до 5,5м. Это и есть модальный интервал.
Его нижняя граница 3,0 величина модального интервала, определяемая как разность между максимальным и минимальным значением признака. равна: 42 -15=27; 42 -19=23.
Следовательно:
Медиана – это значение варьирующего признака, которое делит ранжированный ряд данных на две равные части. Вследствие, 50% единиц исследуемой совокупности имеют значения признака меньше, чем медиана, а 50% - значения признака больше чем медиана.
Если число членов ряда нечетное, медианой будет средний член ряда по порядку: при 9 членах ряда – пятый, при 5 – третий и т.д. Когда число членов ряда четное, медианой является средняя из двух вариант, находящихся в середине ряда.
Когда медиану определяют по несгруппированным (первичным)
данным, сначала необходимо расположить их в порядке возрастания. После определяют номер той единицы, значение признака у которой будет соответствовать медиане: 
,
порядковый номер медианы,
n – число единиц совокупности.
Когда расчет медианы производят по сгруппированным данным, то медиана соответствует варианте, стоящей в середине ранжированного ряда[9]:
,
где - верхняя граница предмедианного интервала;
- частота медианного интервала;
d- величина медианного интервала;
- сумма накопленных частот в интервале, предшествующем медианному.
Медианным называют интервал, кумулятивная (накопленная) частота которого равна или превышает полусумму накопленных частот ряда и ближе всего к ней расположена.
Кумулятивную частоту образуют путем постепенного суммирования частот, начиная с первого интервала.
Далее приведем пример расчета медианы в интервальном ряду на основе данных таблицы 2.
Медианным будет интервал от 3,0 до 5,5. Расчет медианы будет следующий:
Далее необходимо отметить, что медиана обладает свойством, которое заключается в том, что сумма абсолютных величин линейных отклонений от медианы минимальна[10].
Это свойство очень важно при практическом применении медианы.
