Функции алгебры логики (булевы функции)

Таблица 1.5.1 – Значения булевых функций

№ п/п	Значения булевых функций в зависимости от значений аргументов x и y	Обозначение функции	Название функции
	x
	y
	F 0(x, y)						Константа ноль
	F 1(x, y)						Конъюнкция, логическое умножение, И, &, AND
	F 2(x, y)						Запрет по x, отрицание импликации
	F 3(x, y)		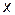				Переменная x
	F 4(x, y)						Запрет по y, отрицание импликации
	F 5(x, y)						Переменная y
	F 6(x, y)						Сумма по модулю 2, логическая неравнозначность, М2, XOR
	F 7(x, y)						Дизъюнкция, логическое сложение, ИЛИ, OR
	F 8(x, y)						Стрелка Пирса, отрицание дизъюнкции, ИЛИ-НЕ, NOT OR
	F 9(x, y)						Эквивалентность
	F 10(x, y)						Отрицание, инверсия y, НЕ, NOT
	F 11(x, y)						Импликация от y к x
	F 12(x, y)						Отрицание, инверсия x, НЕ, NOT
	F 13(x, y)						Импликация от x к y
	F 14(x, y)						Штрих Шеффера, отрицание конъюнкции, И-НЕ, NOT AND
	F 15(x, y)						Константа единица

 

Основные законы алгебры логики

1) Законы нулевого множества:

, , ,

т.е. конъюнкция любого числа переменных обращается в ноль, если хотя бы одна переменная имеет значение 0, независимо от значений других переменных.

2) Законы универсального множества:

, , ,

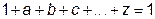т.е. дизъюнкция любого числа переменных обращается в единицу, если хотя бы одна переменная имеет значение 1, независимо от значений других переменных.

3) Законы идемпотентности (повторения, тавтологии):

, .

4) Закон двойной инверсии:

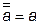, т.е. двойную инверсию можно снять.

5) Законы дополнительности:

· закон логического противоречия

, т.е. конъюнкция любой переменной и ее инверсии есть 0;

· закон исключенного третьего

, т.е. дизъюнкция любой переменной и ее инверсии есть 0.

6) Коммутативные законы (законы перемещения):

,

т.е. результаты выполнения операции конъюнкции и дизъюнкции не зависят от того, в каком порядке следуют переменные.

7) Ассоциативные законы (законы сочетания):

,

т.е. для записи конъюнкции или дизъюнкции скобки можно опустить.

8) Дистрибутивные законы (законы распределения):

· конъюнкции относительно дизъюнкции:

;

· дизъюнкции относительно конъюнкции:

.

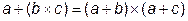9) Законы поглощения:

, .

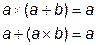10) Законы склеивания (распространения):

, .

11) Законы де Моргана (законы инверсии):

· для двух переменных:

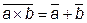, т.е. инверсия конъюнкции есть дизъюнкция инверсий;

, т.е. инверсия дизъюнкции есть конъюнкция инверсий;

· в общем виде:

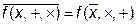или ,

т.е. инверсия функции есть функция от инверсий её аргументов и операций дизъюнкции и конъюнкции.