Упрощенная основная надпись для индивидуальных заданий.

Введение

Рабочая тетрадь составлена в соответствии с типовой программы начертательной геометрии (инженерной графики I), и обеспечивает объем практикума, установленный рабочей программой дисциплины. Она предназначена для проведения аудиторных практических занятий под руководством преподавателя и самостоятельной работы студентов.

Основой таких занятий является решение графических задач, которые способствуют не только закреплению теоретического материала, обучению практическому применению теории, наращиванию знаний, умений и навыков, но и расширяют кругозор студентов, учат логическому мышлению, развивают пространственные представления и пространственное мышление, приводят их в систему. В результате осуществляется подготовка студентов к квалифицированному самостоятельному выполнению расчетно-графических работ по начертательной геометрии и инженерной графике.

Чтобы эффективность учебного процесса была высокой, к каждому практическому занятию студенты должны проработать лекционный материал, изучить по этой же теме материал в учебниках, ответить на контрольные вопросы. В памяти должны быть зафиксированы теоремы, определения, правила, выводы, особое внимание следует обратить на правильную терминологию.

Рекомендации к успешному решению задачи.

Прежде чем приступить к решению задачи, нужно тщательно проанализировать условие, т.е. твёрдо усвоить, что дано и что требуется определить. После анализа условия задачи, опираясь на теоретические знания, полученные из лекций и из рекомендуемой литературы, следует построить алгоритм решения задачи вначале для пространства, а затем и для чертежа. Лишь после этого следует приступать к графическому решению задачи. Таким образом, решение любой задачи сводится к следующему:

- тщательный анализ условия задачи;

- составление алгоритма решения задачи для пространства;

- составление алгоритма решения задачи на эпюре;

- графическое решение задачи.

Решение графических задач студенты выполняют в предлагаемой рабочей тетради для практических занятий. Графические построения необходимо выполнять аккуратно, при помощи чертежных инструментов, черными или цветными карандашами (или пастой). Цветные карандаши (или пасту) используют для выделения искомого результата. Построения выполняются сплошными тонкими линиями. Выполнение построений без чертежных инструментов не допускается. Все буквенные и цифровые обозначения следует выполнять чертежным шрифтом.

ТЕМА «ОСНОВНЫЕ ПРАВИЛА ВЫПОЛНЕНИЯ ЧЕРТЕЖЕЙ»

Форматы чертежей. Оформление чертежных листов. Масштабы. Шрифты чертежные. Линии чертежа. Нанесение размеров.

1. ГОСТ 2.301-68 устанавливает форматы листов чертежей

А0 - 841 х 1189; А1 - 594 х 841; А2 - 420 х 594; А3 - 297 х 420; А4 - 210 х 297 - только вертикально

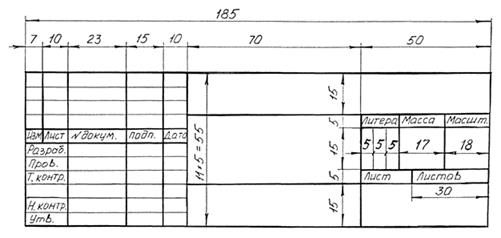
Основная надпись по ГОСТ 2.104 – 68 (рис.1). На всех конструкторских документах в правом нижнем углу помещают основную надпись. На листах формата А4 основную надпись располагают только вдоль короткой стороны, а на листах других форматов – справа вдоль короткой или длинной стороны листа. В ГОСТ 2.104 – 68 описано назначение всех граф основной надписи и указан порядок их заполнения в производственных условиях.

Рис. 1

Упрощенная основная надпись для индивидуальных заданий.

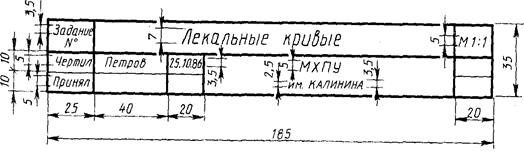
Рис.2

2. ГОСТ 2.302-68 устанавливает масштабы изображений

Масштабы уменьшения 1:2 1:2,5 1:4 1:5 1:10 1:15 1:20 1:25 1:40 1:50 1: 75 1:100 1:200 1:400 1:500 1:800 1:1000

Масштабы увеличения 2:1 2,5:1 4:1 5:1 10:1 20:1 40:1 50:1 100:1 Натуральная величина 1:1

Масштаб, указанный в графе основной надписи, обозначается по типу 1:1, 2:1 и т.д. Масштаб на чертеже указывается по типу М1:2, М2:1 и т.д.

3. ГОСТ 2.303-68 устанавливает начертание и основные назначения линий на чертежах

Наименование	Начертание	Толщина линии по отношению к толщине основной линии	Основное назначение
Сплошная толстая основная		sот 0,5 до 1,4 мм	Линии видимого контура
Сплошная тонкая		От s/3 до s/2	Линии размерные и выносные Линии штриховки
Штриховая		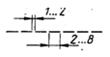От s/3 до s/2	Линии невидимого контура
Штрихпунктирная тонкая		От s/3 до s/2	Линии осевые и центровые
Штрихпунктирная с двумя точками тонкая		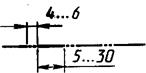От s/3 до s/2	Линии сгиба на развертках

4. ГОСТ 2.304-81 устанавливает чертежные шрифты (рис.3).

Размер шрифта h величина прописных букв в миллиметрах - 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40. Толщина буквы d=1/10 h

Рис.3.

ТЕМА «ПОСТРОЕНИЕ АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ

ГЕОМЕТРИЧЕСКИХ ФИГУР»

Вопросы:

1. Что такое аксонометрия?

2. Что такое коэффициент искажения?

3. Какие виды аксонометрии вы знаете?

4. Как располагаются оси прямоугольной изометрии? Чему равны натуральные и приведенные коэффициенты искажения?

5. Как располагаются оси прямоугольной диметрии? Чему равны натуральные и приведенные коэффициенты искажения?

6. Как располагаются оси косоугольной диметрии? Чему равны натуральные и приведенные коэффициенты искажения?

7. Чему равны большая и малая оси эллипса в прямоугольной изометрии? в прямоугольной диметрии?

Задача 1. Построить аксонометрическую проекцию окружности диаметром 20мм.
А) в прямоугольной изометрии	Б) в прямоугольной диметрии

Выполнение индивидуального задания 1. Формат А4. Вычертить три плоских многоугольника и построить их аксонометрические проекции. Первую фигуру в прямоугольной изометрии (на плоскости П₁), вторую – в прямоугольной диметрии (на плоскости П₂), третью – во фронтальной диметрии(на плоскости П₃). Вариант задания преподаватель выдает на занятии.

ТЕМА «ПРОЕКЦИИ Т ОЧКИ»

Вопросы

1. Что обозначает выражение "ортогональное проецирование"?

2. Что такое Эпюр Монжа?

3. Перечислите все элементы эпюра точки.

4. Присутствует ли сам объект на эпюре?

5. Что такое линия проекционной связи?

6. Сколько проекций необходимо для определения точки в пространстве

7. Какая графическая особенность в изображении точки, принадлежащей плоскости проекций?

8. Какие точки называются конкурирующими? Как определить видимость конкурирующих точек? Как обозначить видимость конкурирующих точек?

Задача 2.Построить по координатам проекции точек А, В, С и D: А (25, 10, 30); В (25, 40, 30); С (40, 25, 45); D (40, 25, 10). Какие точки являются конкурирующими? Показать видимость точек в плоскости П₁ и П₂_.

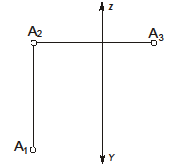
Задача 3. Определить положение недостающих осей, если точка В принадлежит П1.	Задача4. Определить положение оси xy. Записать координаты точек

Выполнение индивидуального задания 2. Формат А4. По заданным координатам точек Аи В построить их проекции в системе трех плоскостей проекций и в прямоугольной изометрической проекции. Определить, как расположена каждая точка относительно плоскостей проекций.

ТЕМА «ПРЯМАЯ ЛИНИЯ»

ВОПРОСЫ

1. Сколько проекций точек необходимо, чтобы задать прямую на чертеже (эпюре?)

2. Сформулируйте свойство принадлежности точки прямой линии.

3. Перечислите линии уровня и укажите их графические признаки.

4. Какие прямые называют проецирующими? Перечислите их графические признаки.

5. На основании теоремы прямого угла сформулируйте графический признак изображения прямого угла на эпюре.

6. Как отличить на эпюре пересекающиеся прямые от скрещивающихся?

7. Какие точки называются точками кажущегося пересечения?

8. Как определить натуральную величину отрезка методом прямоугольного треугольника?

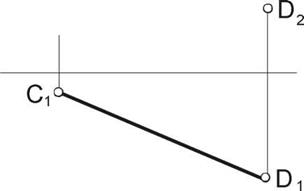
Задача 6. Построить недостающую проекцию отрезка СD, если угол наклона прямой к П₁ =30⁰.	Задача 7. Построить недостающую проекцию отрезка АВ, если его длина равна 60 мм.
	за 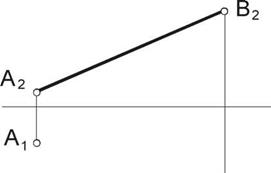д
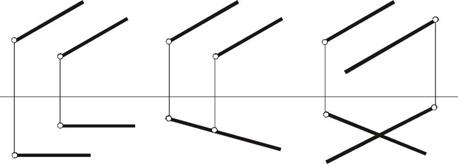
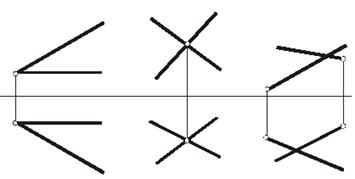
Задача 8.Определить взаимное положение прямых. На скрещивающихся прямых отметить конкурирующие точки (или точки кажущегося пересечения). Определить их видимость.


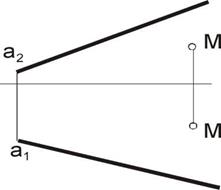
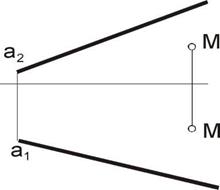
Задача 9. Через точку М провести горизонталь h, пересекающую прямую а.	Задача 10. Через точку М провести прямую m, параллельную а.

Индивидуальное задание 3. Проекции прямой. По заданным координатам точек построить отрезки АВ и СD в системе трех плоскостей проекций и во фронтальной диметрической проекции. Определить положение отрезкой относительно плоскостей проекции, указать для отрезка АВ проекции, где он изображен без искажения.

ТЕМА «ПРОЕКЦИИ ПЛОСКОСТИ»

ВОПРОСЫ

1. Как можно задать плоскость на чертеже?

2. Какое положение может занимать плоскость относительно плоскостей проекций?

3. Перечислите все виды проецирующих плоскостей

4. Каким свойством обладают плоскости частного положения?

5. Сформулируйте правило принадлежности прямой и точки плоскости.

6. Перечислите и дайте определение главным линиям плоскости. Какие графические признаки используются при построении этих линий?

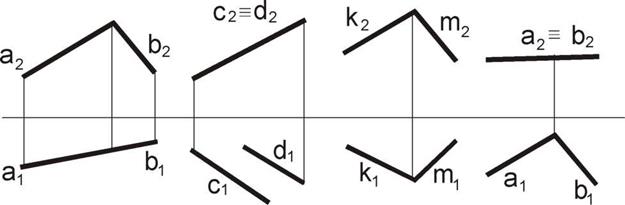Задача 11. Как расположены по отношению к плоскостям проекций плоскости на чертежах а-г. Подписать их названия.

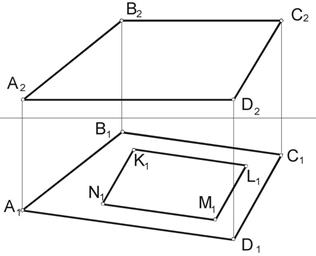
Задача 12. В плоскости ската крыши АВСБ размечен четырехугольник для слухового окна KLMN. Построить его недостающую проекцию.

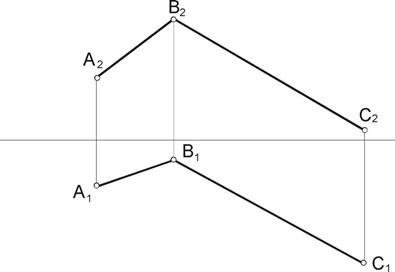
Задача 13.Определить следы плоскости АВС на П₁ и П₂. Через точку А провести горизонталь и фронталь плоскости. Через точку В провести линию наибольшего ската плоскости.

Индивидуальное задание 4. Проекции плоскости. Построить в системе трех плоскостей проекций и в косоугольной диметрической проекции две плоские фигуры по координатам их вершин. Определить положение фигур относительно плоскостей проекций. Формат А4.

ТЕМА «ПОЗИЦИОННЫЕ И МЕТРИЧЕСКИЕ ЗАДАЧИ»

ВОПРОСЫ

1. Перечислите возможные случаи взаимного расположения прямой и плоскости.

2. Сформулируйте графический признак параллельности прямой и плоскости

3. Сформулируйте графический признак перпендикулярности прямой и плоскости.

4. Сформулируйте графический признак параллельности плоскостей.

5. Сформулируйте графический признак перпендикулярности плоскостей.

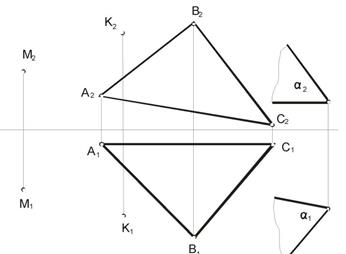
Задача 14. Через точку М провести прямую, параллельную плоскости АВС. Через точку К провести плоскость, параллельную плоскости АВС. Проверить, параллельна ли плоскость α плоскости АВС

Задача 15.Через точку К провести перпендикуляр к плоскости CDE. Через прямую АВ провести плоскость, перпендикулярную плоскости CDE.

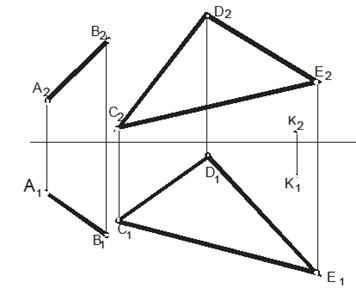
ТЕМА «СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ»

Решение задач.

ВОПРОСЫ

1. Перечислите основные способы преобразования комплексного чертежа.

2. С какой целью применяют преобразование комплексного чертежа?

3. В чем состоит сущность способа замены плоскостей проекций?

4. Что обозначают символы: Х₁₂; Х₁₄; Х₄₅

5. В чем состоит суть способа вращения?

6. Как расположена ось, относительно которой производят вращение?

7. С какой целью применяют плоско- параллельное перемещение?

8. Есть ли какая то связь между методом плоско- параллельного движения и методом замены плоскостей?

Задача 16. Определить расстояние между скрещивающимися прямыми(способом замены плоскостей проекций).

Задача 17. Определить натуральную величину отрезка АВ и углы его наклона к плоскостям П1 и П₂ (способом вращения).

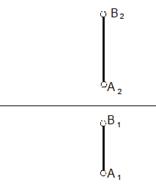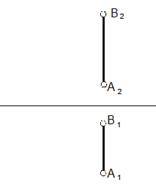
Индивидуальное задание 5. Способы преобразования. По заданным координатам точек построить горизонтальную и фронтальную проекции отрезка АВ и определить его истинную длину способом замены плоскостей проекций и способом вращения. Формат А4.

ТЕМА «КРИВЫЕ ЛИНИИ»

Выполнение индивидуального задания 6.

ВОПРОСЫ

1. В чем различие между плоской и пространственной линиями?

2. Какие вы знаете плоские кривые линии? Пространственные кривые?

3. В чем сущность винтового движения?

Индивидуальное задание 6. Циркульные и лекальные кривые. Вычертить в масштабе 1:1 две циркульные и две лекальные кривые. Два формата А4. Вариант задания преподаватель выдает на занятии.

ТЕМА «ПОСТРОЕНИЕ ПРОЕКЦИЙ ГРАННЫХ ПОВЕРХНОСТЕЙ, НАХОЖДЕНИЕ ПРОЕКЦИЙ ТОЧЕК, ПРИНАДЛЕЖАЩИХ ПОВЕРХНОСТЯМ»

ВОПРОСЫ

1. Многогранники и их виды.

2. Способы построения фигуры сечения многогранника плоскостью.

3. Алгоритм решения задач по нахождению точек встреч прямой с многогранником.

4. Алгоритм решения задач на взаимное пересечение многогранников.

5. Что называется развёрткой многогранника?

Задача 20. Построить проекции пирамиды SABC, у которой основание лежит на плоскости П₁, высота h равна 40 мм, а точка М принадлежит ребру SB. Построить недостающую проекцию точки N, принадлежащей грани ASB. Установить видимость ребер пирамиды.

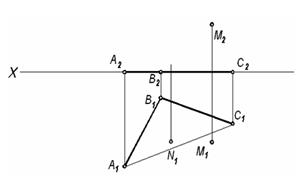
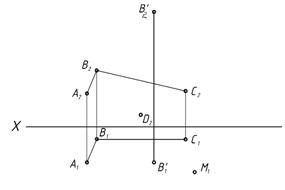
Задача 19. Построить проекции призмы ABCDA^/ B^/C^/ D^/. Определить видимость ребер и сторон основания. Найти фронтальную проекцию т. М, принадлежащей грани CD C^/ D^/.

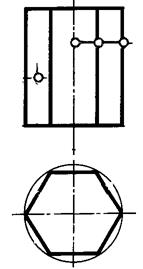
Задача 20. Построить два заданных геометрических тела в системе трех плоскостей проекций, определить проекции заданных точек и отрезков линий.

Индивидуальное задание 7. Проецирование группы геометрических тел. Построить в системе трех плоскостей проекций и в прямоугольной изометрической проекции заданную группу тел. Формат А4. Задание выдает преподаватель на занятии.

ТЕМА «ПОСТРОЕНИЕ ПРОЕКЦИЙ КРИВЫХ ПОВЕРХНОСТЕЙ, НАХОЖДЕНИЕ ПРОЕКЦИЙ ТОЧЕК, ЛИНИЙ, ПРИНАДЛЕЖАЩИХ ПОВЕРХНОСТЯМ. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ И ПРЯМОЙ ЛИНИЙ»

ВОПРОСЫ

1. Перечислите виды поверхностей, которые вы знаете.

2. Какие элементы участвуют в образовании этих поверхностей?

3. Что такое определитель поверхности? Какие элементы составляют определитель поверхности?

4. Чем очерк отличается от каркаса?

5. Перечислите основные виды поверхностей с плоскостью параллелизма. Как они образуются?

6. Перечислите главные линии поверхности вращения

7. Как найти недостающую проекцию точки, лежащей на поверхности вращения?

8. Как образуется поверхность геликоида?

9. Какие точки являются главными (или опорными, или характерными)?

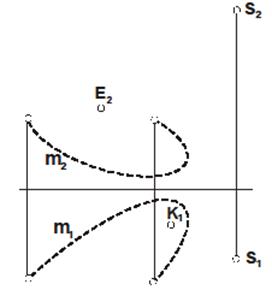
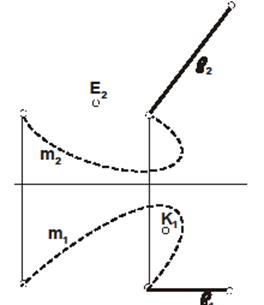
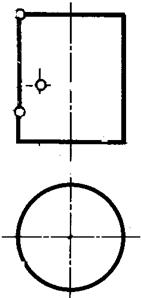
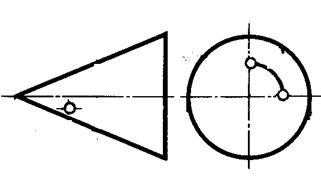
Задача 21. Построить очерк и каркас конической поверхности, Δ(m,ℓ,S). Найти недостающие проекции. Найти недостающие проекции точек Е и К, принадлежащих конической проекции. Определить видимость поверхности очерковых линий.	Задача 22. Построить очерк и каркас цилиндрической поверхности, Δ(m,ℓ). Найти недостающие проекции точек Е и К, принадлежащих поверхности. Определить видимость очерковых линий.

Задача 23. Построить два заданных геометрических тела в системе трех плоскостей проекций, определить проекции заданных точек и отрезков линий.

Индивидуальное задание 8. Усеченный шар. Построить заданный усеченный шар в системе трех плоскостей проекций. Вариант выдает преподаватель на занятии. Формат А4.

ТЕМА «ПОЗИЦИОННЫЕ ЗАДАЧИ НА ПОВЕРХНОСТЯХ»

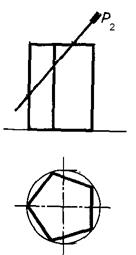
Задача 24. Построить усеченную призму в системе трех плоскостей проекций, определить истинную величину фигуры сечения, вычертить развертку усеченной призмы.

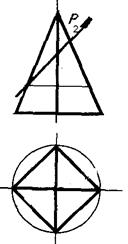
Задача 25. Построить усеченную пирамиду в системе трех плоскостей проекций, определить истинную величину фигуры сечения, вычертить развертку усеченной пирамиды.

Задача 26. Построить усеченный цилиндр в системе трех плоскостей проекций, определить истинную величину фигуры сечения, вычертить развертку усеченного цилиндра.

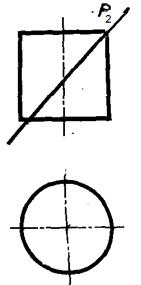
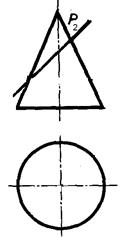
Задача 27. Построить усеченный конус в системе трех плоскостей проекций, определить истинную величину фигуры сечения, вычертить развертку усеченного конуса.

ТЕМА «ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ»

ВОПРОСЫ

1. Перечислите возможные виды пересечения двух поверхностей.

2. Какой вид имеет линия пересечения:

а) двух гранных поверхностей

б) двух кривых поверхностей

в) гранной и кривой поверхностей.

3. В каком случае задача нахождения линии пересечения упрощается?

4. В каком случае целесообразно применять способ вспомогательных проецирующих секущих плоскостей? Алгоритм нахождения линии пересечения.

5. Какие точки линии пересечения являются характерными (опорными или главными)?

6. В каких случаях применяется способ вспомогательных концентрических сфер?

7. На каком свойстве основан способ вспомогательных сфер?

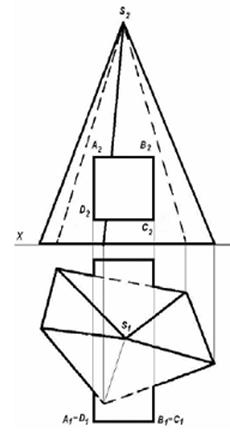
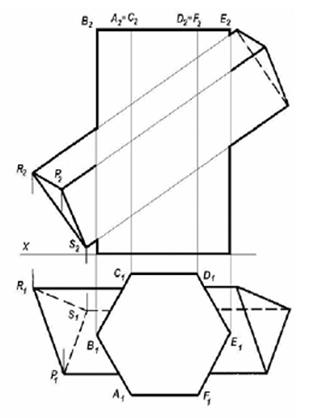
Задача28. Построить линию пересечения многогранников.

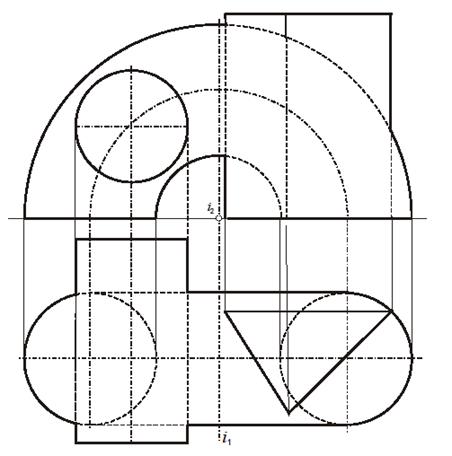
Задача 29. Построить линии пересечения 3-х поверхностей. Определить видимость

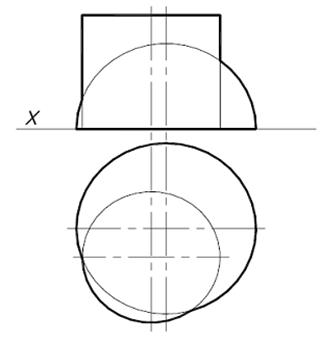
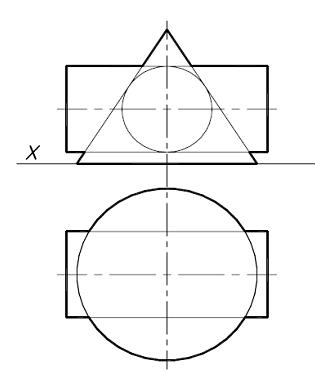
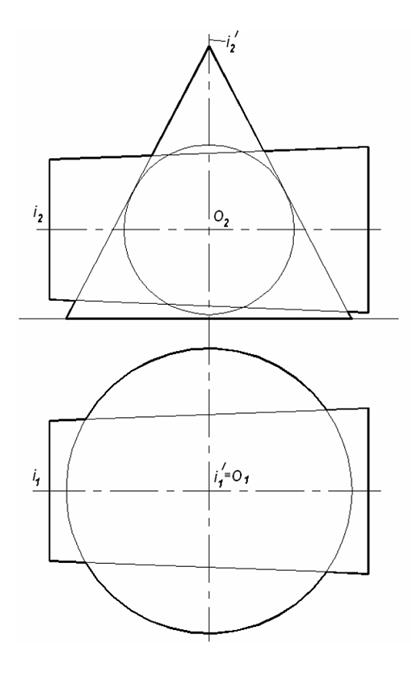
Задача 30. Построить линии пересечения заданных поверхностей.

Рекомендуемая литература:

1. Н.Н. Крылов и др. «Начертательная геометрия». М.:Высшая школа, 1990.

2. Будасов Б.В., Каминский В.П. «Строительное черчение». М.: Стройиздат, 1990.

3. Ю.И. Короев «Начертательная геометрия». М.:Стройиздат, 1987

4. С.А. Фролов «Сборник задач по начертательной геометрии», М.: Высшая школа, 1980