СИНТЕЗ РЕКУРРЕНТНОГО АЛГОРИТМА
ЧЕТНОГО ПОЛОСОВОГО ФИЛЬТРА И ЕГО МОДЕЛИРОВАНИЕ
Методические указания к выполнению
лабораторной работы по дисциплине
«ТЕОРИЯ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ.
МЕТОДЫ РАСЧЕТА И ПРОЕКТИРОВАНИЯ САУ»
для студентов специальности 190302 «Вагоны»
всех форм обучения
(4 часа)
Составители: Т.Н. Буштрук
Самара 2015
УДК 681.51.015
Исследование цифровых алгоритмов типовых звеньев: методические указания к выполнению лабораторной работы по дисциплине «Системы автоматизации производства и ремонта вагонов» для студентов специальности 190302 всех форм обучения / Т.Н. Буштрук. – Самара: СамГУПС, 2015. – 10 с.
Утверждены на заседании кафедры «Вагоны» 00.00.2015, протокол № 00.
Печатаются по решению редакционно-издательского совета СамГУПС.
Данное методическое указание разработано в учебно-исследовательской лаборатории «Моделирования систем управления и телекоммуникаций».
Методические указания предназначены для студентов, изучающих дисциплину «Системы автоматизации производства и ремонта вагонов» специальности 190302 всех форм обучения.
Составители: Буштрук Татьяна Николаевна
Рецензенты: д.т.н., профессор, заведующий кафедрой «Мехатроника в автоматизированных производствах» О.А. Кацюба;
к.т.н., доцент, заведующий кафедрой «Автоматика, телемеханика и связь
на железнодорожном транспорте» В.Б. Гуменников
Редактор И.А.Шимина
Компьютерная верстка Е.Ю. Шарова
Подписано в печать10.04.2008. Формат 60x84 1/16.
Бумага писчая. Печать оперативная. Усл. п. л. 0,65.
Тираж 100 экз. Заказ № 44.
© Самарский государственный университет путей сообщения, 2015
СИНТЕЗ РЕКУРРЕНТНОГО АЛГОРИТМА
ЧЕТНОГО ПОЛОСОВОГО ФИЛЬТРА
ДЛЯ КОРРЕЛЯЦИОННО-СПЕКТРАЛЬНОГО АНАЛИЗАТОРА
Введение. В работе [1] описан корреляционно-спектральный метод идентификации квазистационарных процессов сориентированных на применение в системах прогнозирования технических, социальных, геофизических и экономических процессов.
Основными элементами устройств идентификации квазистационарных временных процессов являются четные полосовые фильтры, требования к которым достаточно высоки. Такие фильтры описаны в ряде работ, например в [2,3], однако, фильтры, описанные в них, имеют большое число настроечных параметров (см. [3]). В предлагаемых алгоритмах, обеспечивающих цифровую фильтрацию временных процессов, эти недостатки отсутствуют. В основу синтеза рекуррентных алгоритмов четного полосового фильтра положен метод Z-преобразования, описанный в [4].
Рекуррентный алгоритм. Передаточная функция для четного полосового фильтра имеет вид:
 .
.
Коэффициенты полиномов А 0 и В 0 имеют размерность [Гц2], А 1 и В 1 – [Гц].
При отсутствии кратных полюсов у передаточной функции системы формула для импульсной переходной характеристики является суперпозицией экспонент:
 ,
,
где  .
.
В соответствии с методом Z - преобразования передаточная функция эквивалентной импульсной системы для четного полосового фильтра определяется соотношением:
 ,
,
где  ,
,  .
.
Тогда:
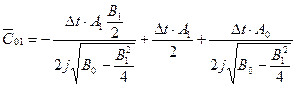 ;
;
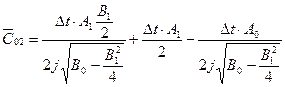 ;
;
 ;
;

 ;
;
 ;
;
 .
.
Рекуррентный алгоритм имеет вид:

+ 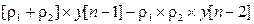 ,
,
при начальных условиях х [0] = x [-1] = y [0] = y [-1] = y [-2] = 0.

.
Передаточную функцию W(S) запишем в следующем виде:
 ,
,
где 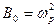 [Гц2],
[Гц2], 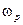 - резонансная частота четного полосового фильтра,
- резонансная частота четного полосового фильтра,
С = А 0/ В 0, а А 0= С · В 0, С- масштабный коэффициент. Перепишем W(S) в следующем виде:
 .
.
Учитывая, что Dw=wр/ Q, Δ ω – полоса пропускания фильтра на уровне 0.707,
Q – добротность, получим:
 .
.
Вводя отношения m = B 1/Dw,  , где m и d – масштабные коэффициенты, получим:
, где m и d – масштабные коэффициенты, получим:
 .
.
Далее определяем корни характеристического уравнения:
 .
.
Они имеют вид:
 ,
,
 .
.
Для осуществления нормировки четного полосового фильтра определяем импульсно-переходную функцию:
 ,
,
где L -1[·]- обратное преобразование Лапласа. Производная от характеристического полинома имеет вид:
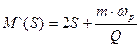 ,
,
 ,
,
 ;
;
С учетом всех подстановок импульсная – переходная характеристика имеет вид:

 .
.
С ростом Q вклад синусоидальных компонент уменьшается.
Условие нормировки:
 [ рад / сек ],
[ рад / сек ],  [ рад ],
[ рад ],
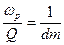 [ рад / сек ],
[ рад / сек ],  [ рад ],
[ рад ],
 [ рад ],
[ рад ],  [ рад ].
[ рад ].
При высоких добротностях выражение для импульсной - переходной функции нормированного четного полосового фильтра имеет вид:
 [ рад / сек ],
[ рад / сек ],
где Q/m = (2p · d)/(D t · N) [ рад ].
С условием нормировки формула для передаточной функции четного полосового фильтра принимает вид:
 .
.
Рекуррентный алгоритм для нормированного четного полосового фильтра имеет вид:

Результаты моделирования. Результаты расчета проверки работоспособности алгоритма приведены в таблицах 1, 2 и 3 и на рисунках при воздействии сигнала вида d-функция.
В таблице 1 приведены данные моделирования фильтра с параметрами Q = 20, N = 32, m = 1, C = 0.
Таблица 1
| n | 
| n | 
| n | 
| n | 
| n | 
|
| 4,8557 | -2,416 | -0,887 | 3,1256 | -3,282 | |||||
| 4,0286 | -0,767 | -2,324 | 3,6149 | -2,729 | |||||
| 2,6103 | 0,9646 | -3,383 | 3,5497 | -1,776 | |||||
| 0,8260 | 2,5181 | -3,910 | 2,9506 | -0,573 | |||||
| -1,048 | 3,6618 | -3,838 | 1,9184 | 0,6921 | |||||
| -2,727 | 4,2312 | -3,189 | 0,6170 | 1,8289 | |||||
| -3,963 | 4,1516 | -2,071 | -0,752 | 2,6679 | |||||
| -4,577 | 3,4477 | -0,663 | -1,981 | 3,0883 | |||||
| -4,489 | 2,2377 | 0,8171 | -2,887 | 3,0350 | |||||
| -3,726 | 0,7139 | 2,1460 | -3,341 | 2,5251 |

Рисунок -1. Результаты моделирования фильтра с параметрами Q = 20, N = 32, m = 1, C = 0.
В таблице 2 приведены результаты моделирования с параметрами фильтра Q = 5, N = 32, m = 1, C = 0.
Таблица 2
| 4,7138 | -1,622 | -0,569 | 1,2941 | -1,000 | |||||
| 3,6651 | -0,379 | -1,301 | 1,4403 | -0,808 | |||||
| 2,1591 | 0,8260 | -1,788 | 1,3646 | -0,513 | |||||
| 0,4506 | 1,8194 | -1,976 | 1,0948 | -0,164 | |||||
| -1,194 | 2,4713 | -1,861 | 0,6851 | 0,1815 | |||||
| -2,540 | 2,7121 | -1,481 | 0,2060 | 0,4750 | |||||
| -3,413 | 2,5376 | -0,914 | -0,267 | 0,6767 | |||||
| -3,720 | 2,0048 | -0,255 | -0,665 | 0,7641 | |||||
| -3,459 | 1,2186 | 0,3907 | -0,936 | 0,7330 | |||||
| -2,711 | 0,3134 | 0,9309 | -1,049 | 0,5970 |

Рисунок. – 2 Результаты моделирования фильтра с параметрами Q = 5, N = 32, m = 1, C = 0.
В таблице 3 приведены результаты моделирования с параметрами фильтра Q = 2, N = 32, m = 1, C = 0;
Таблица 3
| 4,4424 | -0,829 | -0,132 | 0,1949 | -0,096 | |||||
| 3,0306 | -0,145 | -0,339 | 0,2212 | -0,083 | |||||
| 1,4517 | 0,4374 | -0,462 | 0,2122 | -0,060 | |||||
| -0,046 | 0,8556 | -0,499 | 0,1755 | -0,033 | |||||
| -1,271 | 1,0811 | -0,461 | 0,1211 | -0,006 | |||||
| -2,101 | 1,1169 | -0,365 | 0,0596 | 0,0160 | |||||
| -2,493 | 0,9919 | -0,236 | 0,0008 | 0,0327 | |||||
| -2,471 | 0,7521 | -0,098 | -0,047 | 0,0418 | |||||
| -2,111 | 0,4511 | 0,0294 | -0,080 | 0,0436 | |||||
| -1,523 | 0,1414 | 0,1301 | -0,096 | 0,0390 |

Рисунок. -3 Результаты моделирования фильтра с параметрами Q = 2, N = 32, m = 1, C = 0.
В таблице 1 Q =20, N =32, m =1, C =0; в таблице 2 Q =5, N =32, m =1, C =0; в таблице 3 Q =2, N =32, m =1, C =0;
Теоретическая часть
Передаточная функция для звена любого порядка имеет вид
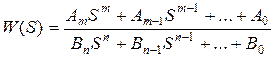 , где n>m.
, где n>m.
От передаточной функции W(S) необходимо перейти к передаточной функции эквивалентной импульсной системы:
 .
.
По известным коэффициентам Am, Am-1,…,A0 и Bn, Bn-1,…, B0 можно определить коэффициенты a0, a1,…,a l и b1,…,b k. Используя передаточную функцию эквивалентной импульсной системы, находят разностное уравнение (рекуррентный алгоритм) для моделирования линейных динамических звеньев в классе дробно рациональных передаточных функций.
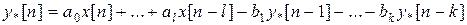 .
.
Символ * обозначает, то что эквивалентная импульсная система имеет такие же свойства, как и непрерывная система. Начальные условия задаются следующими формулами x[0]=0, x[-1]=0, x[- l ]=0, y[0]=0, y[-1]=0, y[- k ]=0.
В основу синтеза рекуррентных алгоритмов положен метод z-преобразования. При отсутствии кратных полюсов у передаточной функции системы формула для импульсной переходной характеристики является суперпозицией экспонент:
 ,
,
где  .
.
В соответствии с методом z - преобразования передаточная функция эквивалентной импульсной системы определяется соотношением:
 ,
,
где  ,
,  .
.
В лабораторной работе рассматриваются следующие звенья с передаточными функциями и строятся рекуррентные алгоритмы:
1) Звено первого порядка. Для него имеем:
 .
.
Приравнивая знаменатель этого выражения к нулю, находим корень характеристического уравнения:
 .
.
Тогда для звена первого порядка получим:
 ;
;  ,
,
где  тогда
тогда  .
.
 ,
,  ,
,  .
.
С учетом полученных выражений разностное уравнение для звена первого порядка имеет вид
 .
.
Время переходного процесса для звена первого порядка определяется по следующей формуле:
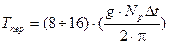 .
.
2) Звено второго порядка, передаточная функция которого имеет вид
 ,
,
корни характеристического уравнения принимают значения:  ,
,  . С учетом метода z-преобразования имеем:
. С учетом метода z-преобразования имеем:
 ;
;
 ;
;
 ;
;
 ;
;
где  - относительное время,
- относительное время,  .
.
 , при C >1.
, при C >1.
С учетом проведенных преобразований записываем передаточную функцию эквивалентной импульсной системы для звена второго порядка

 ,
,  ,
,
по которой определяется разностное уравнение:
 .
.
Отсюда окончательно получаем:

 .
.
В лабораторной работе рассматривается также вариант передаточной функции для звена второго порядка следующего вида:
 .
.
Эта передаточная функция описывает важный класс звеньев второго порядка типа четных полосовых фильтров. Для нее корни характеристического уравнения имеют вид
 ,
,  .
.
Параметры разностных уравнений определяются следующими формулами:
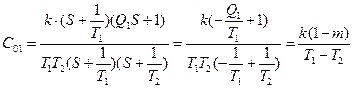 ;
;
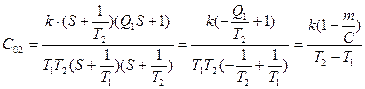 ;
;
 ;
;
 ;
;
где  тогда
тогда 
 , при C >1
, при C >1
 .
.
С учетом полученных коэффициентов передаточная функция эквивалентной импульсной системы принимает следующий вид:
 ,
,
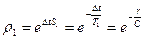 ,
,  .
.
От эквивалентной импульсной системы осуществляется переход к разностному уравнению:

 .
.
Передаточная функция для звена второго порядка может быть представлена еще в одном виде, удобном для физической интерпретации процессов:
 ,
,
где 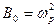 [Гц2]. Вводя обозначения,
[Гц2]. Вводя обозначения,  , => (следовательно)
, => (следовательно)  , получим:
, получим:
 .
.
Учитывая связь между полосой пропускания (определяемой на уровне 0.707) и добротностью,
 ,
,
где Δ ω – полоса пропускания, Q – добротность. Окончательно получим:
 ,
,
где  ;
;  .
.
Далее определяем импульсно-переходную функцию:
 ,
,
где N (S) и M (S) соответственно полиномы числителя и знаменателя W (S), M `(S) производная по S
Отсюда имеем:

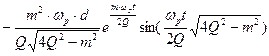 .
.
Для четного полосового фильтра с ростом Q вклад синусоидальных компонент уменьшается.
Условие нормировки для четного полосового фильтра определяется следующими соотношениями:
 [ рад / сек ]
[ рад / сек ]  [ рад ]
[ рад ]
 [ рад / сек ]
[ рад / сек ]  [ рад ]
[ рад ]
 [ рад ];
[ рад ];  ,
,
где ωр ×Dt=2×p/N, Dt – шаг дискретизации по времени.
da – коэффициент прорежения; g – коэффициент запаса.
 [1/ сек ].
[1/ сек ].
По степени экспоненты  определяется время переходного процесса как в четном, так и нечетном фильтрах. Отсюда имеем:
определяется время переходного процесса как в четном, так и нечетном фильтрах. Отсюда имеем:
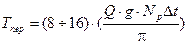 .
.
Время переходного процесса полосового фильтра определяется с инженерной точностью.
Условие нормировки для нечетного полосового фильтра определяется следующими соотношениями
С условием нормировки формула для передаточной функции четного полосового фильтра принимает вид
С условием нормировки формула для передаточной функции нечетного полосового фильтра принимает вид






