Лекція
Тема: Основні теореми диференціального обчислення
Ціль: Розглянути основні теореми диференціального обчислення, а також їхнє застосування на практиці.
План: 1. Правило Лопиталя
2. Теорема Ферма.
3. Теорема Роля.
4. Теорема Коші.
5. Теорема Лагранжа.
Правило Лопиталя
Функція 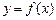 , певна у всіх точках проміжку
, певна у всіх точках проміжку 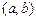 , називається зростаючої (убутної) у цьому проміжку, якщо для будь-яких двох значень аргументу, що належать цьому проміжку, більшому з них відповідає більше (менше) значення функції, т. е,
, називається зростаючої (убутної) у цьому проміжку, якщо для будь-яких двох значень аргументу, що належать цьому проміжку, більшому з них відповідає більше (менше) значення функції, т. е,
якщо 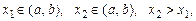 то при
то при
 – зростаюча,
– зростаюча,  – убутна.
– убутна.
З даного визначення випливає, що для зростаючої функції приросту аргументу й функції має той самий знак, у силу чого їхнє відношення позитивно: 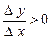 . Для убутної функції ці прирости мають різні знаки, у силу чого
. Для убутної функції ці прирости мають різні знаки, у силу чого 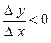 . Ті значення аргументу, при яких функція досягає своїх найбільших і найменших у порівнянні із близькими значень, називаються точками максимуму й мінімуму (точками екстремуму).
. Ті значення аргументу, при яких функція досягає своїх найбільших і найменших у порівнянні із близькими значень, називаються точками максимуму й мінімуму (точками екстремуму).
 Точка
Точка 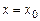 називається точкою максимуму (мінімуму) безперервної функції
називається точкою максимуму (мінімуму) безперервної функції 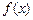 , а значення
, а значення 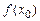 називається максимумом (мінімумом) цієї функції, якщо існує деяка околиця точки
називається максимумом (мінімумом) цієї функції, якщо існує деяка околиця точки 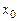 така, що значення функції в будь-якій точці цієї околиці буде менше (більше), чим її значення в самій точці
така, що значення функції в будь-якій точці цієї околиці буде менше (більше), чим її значення в самій точці 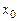 , тобто менше (більше), чим максимум (мінімум)
, тобто менше (більше), чим максимум (мінімум) 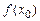 (мал. 1).
(мал. 1).
у max у
min
f (х 0) f (х 0)
О х 0–d х 0 х 0+d х О х 0–d х 0 х 0+d х
| точка максимуму | точка мінімуму |
Рис. 1
З визначень точок екстремуму треба, що поза (-околиці точки екстремуму поводження функції довільно, тобто поняття максимуму й мінімуму функції носять характер локальних (місцевих), а не абсолютних понять.
Щоб установити ознаки зростання й убування й ознаки екстремуму функцій, розглянемо ряд важливих теорем математичного аналізу, на які опираються всі подальші дослідження функцій.
Теорема Ферма. Якщо функція 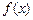 безперервна в проміжку
безперервна в проміжку 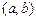 , у деякій внутрішній точці х 0 цього проміжку досягає максимуму (або мінімуму) і дифференцьована в цій точці, то її похідна в цій точці дорівнює нулю:
, у деякій внутрішній точці х 0 цього проміжку досягає максимуму (або мінімуму) і дифференцьована в цій точці, то її похідна в цій точці дорівнює нулю:  .
.
Припустимо для визначеності, що х 0 – точка максимуму. Тоді для будь-якої точки 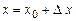 з інтервалу
з інтервалу 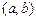 виконується нерівність
виконується нерівність 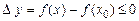 . Тому
. Тому 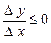 , якщо
, якщо 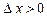 й
й 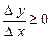 , якщо
, якщо 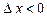 . Переходячи до меж, одержимо
. Переходячи до меж, одержимо
 и.
и. 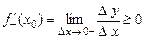
Обоє нерівності будуть виконуватися, якщо  .
.
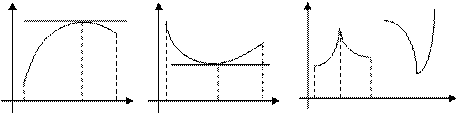
Геометричний зміст теореми Ферма полягає в тому, що дотична до графіка функції 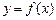 в точці
в точці 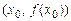 паралельна осі Ох, якщо х 0 – точка максимуму або мінімуму функції
паралельна осі Ох, якщо х 0 – точка максимуму або мінімуму функції 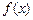 на інтервалі
на інтервалі 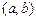 (мал. 2).
(мал. 2).
У точці максимуму (мінімуму) х 0 похідна 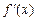 може не існувати (мал. 3)
може не існувати (мал. 3)
 у max у
min
f (х 0) f (х 0)
О a х 0 b х О a х0 b х
Рис. 2 у max у
min
f (х 0) f (х 0)
О a х 0 b х О a х0 b х
Рис. 2
| у max min О a х 0 b х Рис. 3 |
Теорема Роля. Нехай функція 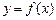 :
:
1) безперервна на відрізку 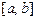 ;
;
2) дифференцьована на інтервалі 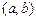 ;
;
3) на кінцях відрізка приймає рівні значення 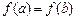 .
.
Тоді існує точка 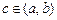 , у якій
, у якій 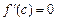 . Тому що функція безперервна на відрізку
. Тому що функція безперервна на відрізку 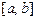 , то вона приймає в деяких точках
, то вона приймає в деяких точках 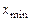 і
і 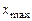 мінімальне й максимальне значення:
мінімальне й максимальне значення: 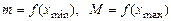 . Якщо
. Якщо 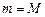 , то
, то 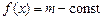 й у будь-якій точці інтервалу
й у будь-якій точці інтервалу 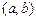 похідна
похідна 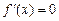 . Тому можемо вважати, що
. Тому можемо вважати, що 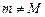 . Покладемо
. Покладемо 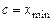 , якщо
, якщо 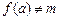 , і
, і 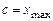 , якщо
, якщо 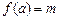 . При такому визначенні з маємо
. При такому визначенні з маємо 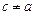 . Оскільки
. Оскільки 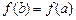 , те
, те 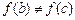 , тому
, тому 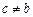 . Отже, з – це точка максимуму або мінімуму функції
. Отже, з – це точка максимуму або мінімуму функції 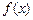 й
й 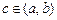 . По теоремі Ферма
. По теоремі Ферма 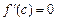 .
.
Геометричний зміст теореми Роля: на графіку функції 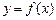 найдеться принаймні одна точка, у якій дотична до графіка паралельна осі Ох.
найдеться принаймні одна точка, у якій дотична до графіка паралельна осі Ох.
В окремому випадку, коли 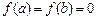 , теоремі Роля можна дати нове тлумачення: між двома нулями дифференцьованой функції завжди укладений принаймні один нуль її похідній.
, теоремі Роля можна дати нове тлумачення: між двома нулями дифференцьованой функції завжди укладений принаймні один нуль її похідній.
Теорема Лагранжа. Нехай функція 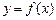 безперервна на відрізку
безперервна на відрізку 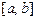 й дифференцируема на інтервалі
й дифференцируема на інтервалі 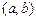 . Тоді існує така точка
. Тоді існує така точка 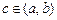 , що
, що
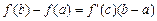 . (2)
. (2)
Формула (4.2) називається формулою кінцевих приростів.
Введемо допоміжну функцію
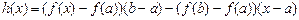 .
.
Тоді
1) 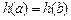 ;
;
2) 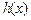 безперервна в тих же точках, у яких безперервна функція
безперервна в тих же точках, у яких безперервна функція 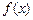 , тобто
, тобто 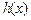 безперервна на
безперервна на 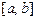 й дифференцьована в.
й дифференцьована в. 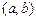 По теоремі Роля, існує точка
По теоремі Роля, існує точка 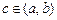 , у якій
, у якій 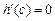 . Тому що
. Тому що 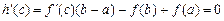 , те в точці з виконується рівність (2).
, те в точці з виконується рівність (2).
Теорема Коші. Нехай функції 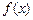 й
й 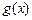 безперервні на відрізку
безперервні на відрізку 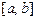 й дифференцьовані на інтервалі
й дифференцьовані на інтервалі 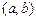 . Нехай, крім того,
. Нехай, крім того, 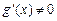 на
на 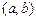 . Тоді існує точка
. Тоді існує точка 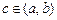 , така, що
, така, що
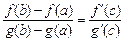 .
.
Теорема Лагранжа є часткою случаємо теореми Коші, коли  .
.
Розкриття невизначеностей за правилом Лопиталя. Розкриттям невизначеностей у математичному аналізі називається відшукання межі 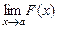 , коли функція
, коли функція 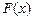 безперервна поблизу точки
безперервна поблизу точки 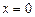 , але не визначена в самій цій точці, а безпосередня підстановка у формулу цієї функції значення
, але не визначена в самій цій точці, а безпосередня підстановка у формулу цієї функції значення 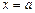 приводить до вираження невизначеного виду:
приводить до вираження невизначеного виду:
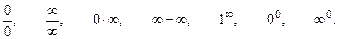
Основними видами невизначеностей є наступні два: 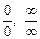 .
.
Для цих двох видів невизначеностей справедлива теорема Лопиталя: межа відносини двох нескінченно малих або нескінченно більших функцій дорівнює межі відносини їхніх похідних
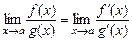 .
.
Правило Лопиталя дозволяє в багатьох випадках знайти межу  виду
виду 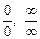 або, як говорять, розкрити невизначеність.
або, як говорять, розкрити невизначеність.
Зауваження 1. Інші види невизначеностей можна звести до основних видів.
Зауваження 2. Правило Лопиталя можна застосовувати повторно.
Приклад. Знайти 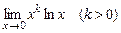 . Це невизначеність виду
. Це невизначеність виду 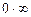 . Представимо дану межу у вигляді
. Представимо дану межу у вигляді 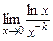 ; це вже буде невизначеність виду
; це вже буде невизначеність виду 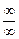 , до якої застосовне правило Лопиталя.
, до якої застосовне правило Лопиталя.
Тому 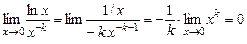 .
.
Завдання для перевірки знань:
1. Дайте формулювання теореми Ферма.
2. Дайте формулювання теореми Ролля.
3. Дайте формулювання теореми Коші.
4. Дайте формулювання теореми Лагранжа.
5. Для чого використовується правило Лопиталя?
Література:
4. «Высшая математика для экономистов» под редакцией Н.Ш. Кремера стр.178-185
5. М.І. Шкіль «Математичний аналіз» стр. 210-220
6. В.М. Лейфура, Г.І. Городницький, Й.І. Фауст «Математика» стр.426-430
Додаткова література:
1. А.Д. Мышкис «Лекции по высшей математике» стр.127-133
2. Л.Д. Кудрявцев «Курс математического анализа» том 1 стр. 159-167
Розділ: «Похідна функції та її застосування»
Лекція
Тема: Дослідження функцій за допомогою похідної
Ціль: Розглянути схему дослідження функцій за допомогою похідної, навчитися практично досліджувати функції будувати графіки
План: 1. Зростання й убування функції
2. Необхідна й достатня умова екстремуму.
3. Опуклість і ввігнутість функції, крапки перегину
4. Асімптоти графіка функція.
5. Загальна схема дослідження функції.
Зростання й убування функції. Екстремум функції.
Асімптоти графіка функції
У попередньому розділі дані визначення понять зростаючої (убутної) функції на проміжку X.
Достатня умова зростання (убування) функції формулюється в такий спосіб: якщо функція 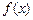 діференцьована в проміжку
діференцьована в проміжку 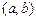 і її похідній у цьому проміжку позитивна (негативна), те сама функція в цьому проміжку зростає (убуває). Доказ даної теореми засновано на застосуванні на відрізку
і її похідній у цьому проміжку позитивна (негативна), те сама функція в цьому проміжку зростає (убуває). Доказ даної теореми засновано на застосуванні на відрізку 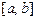 теореми Лагранжа.
теореми Лагранжа.
Необхідна умова екстремуму функції: у точці екстремуму або похідна функції дорівнює нулю, або функція недіференцьована. Точки з області визначення функції, у яких необхідна умова екстремуму виконана, і в які, отже, тільки й можливий екстремум, називаються критичними (або стаціонарними). Помітимо, що зворотне твердження в загальному невірно. Критична точка не обов'язково є точкою екстремуму. Судити про те, буде дана критична точка точкою екстремуму чи ні, можна на підставі достатніх умов екстремуму. Одне з них затверджує, що, якщо при переході через критичну точку похідна функції міняє свій знак із плюса на мінус, те ця точка - точка локального максимуму, а якщо з мінуса на плюс, то точка локального мінімуму. Існують і інші формулювання достатньої умови екстремуму, що використовують поняття вищих похідних.
Варто розрізняти поняття екстремуму функції і її найбільше й найменше значення на заданому відрізку зміни аргументу. Найбільше або найменше значення функції може досягатися як у точках екстремуму, так і на кінцях відрізка. Для відшукання найбільшого (найменшого) значення функції на відрізку варто знайти її похідну, визначити критичні точки, знайти значення функції в цих точках і на кінцях відрізка й вибрати з них найбільше (найменше).
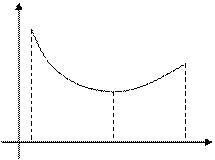
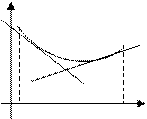
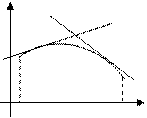
Опуклість і точки перегину графіка функції. Графік функції 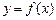 називається опуклим (увігнутим) на проміжку
називається опуклим (увігнутим) на проміжку 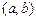 , якщо він розташований не вище (нижче) будь-якій дотичній до графіка функції на
, якщо він розташований не вище (нижче) будь-якій дотичній до графіка функції на 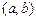 (мал. 1).
(мал. 1).
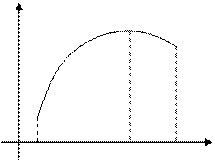
 Точка
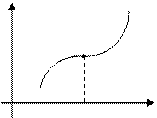
Точка 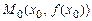 , що розділяє інтервали опуклості й увігнутості, називається точкою перегину графіка функції (мал. 2).
, що розділяє інтервали опуклості й увігнутості, називається точкою перегину графіка функції (мал. 2).
  у
О а b х у
О а b х
| у О a b х | у
 О x 0 х
О x 0 х
|
| Рис. 1 | Рис. 2 |
Достатньою ознакою опуклості (увігнутості) графіка функції усередині деякого проміжку є негативне (позитивне) значення другої похідної даної функції на цьому проміжку.
У точці перегину друга похідна двічі діференцьованої функції дорівнює нулю. Це є необхідною умовою перегину. Достатньою ознакою наявності точки перегину є зміна знака другої похідної функції при переході через дану точку.
Асімптоти графіка функції. У загальній задачі дослідження характеру зміни функції важливе значення має дослідження поводження 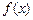 при необмеженому зростанні (по абсолютній величині) аргументу х, а також дослідження випадків необмеженого зростання абсолютної величини
при необмеженому зростанні (по абсолютній величині) аргументу х, а також дослідження випадків необмеженого зростання абсолютної величини 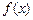 в кінцевій частині області визначення. Геометрично ці дослідження приводять до поняття асімптоти графіка.
в кінцевій частині області визначення. Геометрично ці дослідження приводять до поняття асімптоти графіка.
Асімптотой графіка функції 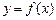 називається пряма лінія, до якої необмежено наближається гілка, що йде в нескінченність, графіка (мал. 3).
називається пряма лінія, до якої необмежено наближається гілка, що йде в нескінченність, графіка (мал. 3).
 Розрізняють три види асімптот: вертикальні, горизонтальні й похилі.
Розрізняють три види асімптот: вертикальні, горизонтальні й похилі.
у
уас
укр
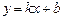
 ПРО х
Рис. 3
ПРО х
Рис. 3
| Нехай пряма 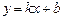 є похилої асімптотой графіка функції є похилої асімптотой графіка функції 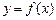 . Для відшукання кутового коефіцієнта k і початкової ординати b асімптоти використовується умова . Для відшукання кутового коефіцієнта k і початкової ординати b асімптоти використовується умова
|
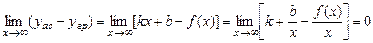 ,
,
звідки
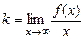 , тому що
, тому що 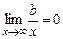 .
.
Далі визначається 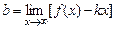 .
.
В окремому випадку 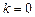 асимптот буде горизонтальною. Пряма
асимптот буде горизонтальною. Пряма 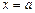 називається вертикальної асімптотой графіка функції
називається вертикальної асімптотой графіка функції 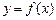 , якщо хоча б одне із граничних значень
, якщо хоча б одне із граничних значень 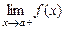 або
або 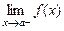 дорівнює
дорівнює 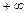 або
або 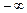 .
.
Загальна схема дослідження поведінки функції й побудови її графіка
Рекомендується дослідження функцій проводити в певній послідовності.
1. Знайти область визначення функції; крапки розриву і їхній характер; вертикальні асімптоти графіка.
2. Визначити можливий тип симетрії функції (парність, непарність функції); крапки перетинання графіка функції з осями координат, тобто вирішити рівняння 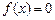 й
й 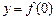 .
.
3. Знайти похилі й горизонтальні асімптоти графіка функції.
4. Використовувати першу похідну для визначення області зростання й убування й екстремумів функції.
5. Використовувати другу похідну для визначення ділянок опуклості й увігнутості графіка й точок перегину.
6. Побудувати графік функції з урахуванням проведеного дослідження.
Завдання для самоперевірки
- Необхідні та достатні умови зростання і убування функції
- Необхідна й достатня умова екстремуму.
- Опуклість і ввігнутість функції, крапки перегину.
- Асімптоти графіка функція.
- Побудувати графік функції
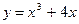
Література:
7. «Высшая математика для экономистов» под редакцией Н.Ш. Кремера стр.212-231
8. М.І. Шкіль «Математичний аналіз» стр. 229-260
9. В.М. Лейфура, Г.І. Городницький, Й.І. Фауст «Математика» стр.432-452
Додаткова література:
1. А.Д. Мышкис «Лекции по высшей математике» стр.142-146
2. Л.Д. Кудрявцев «Курс математического анализа» том 1 стр. 221-248






