Приведём примерный план исследования функций.
1. Определить область существования функции. Область существования функции указывает точки оси аргумента, над которыми пройдёт кривая.
2. Найти точки пересечения графика функции с осями координат.
3. Исследовать функцию на периодичность. Для периодической функции достаточно построить график на промежутке длиной в период.
4. Исследовать функцию на четность и нечетность. Если функция четная или нечетная, то график функции достаточно построить при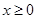 
, а затем отобразить симметрично относительно оси 
в случае чётной функции или относительно начала координат в случае нечётной функции.
5. Найти промежутки возрастания и убывания функции, точки экстремума.
6. Найти промежутки выпуклости и вогнутости графика функции, точки перегиба.
7. Определить асимптоты.
8. Все данные свести в таблицу и построить график.
9. Если полученные результаты не дают ясной картины поведения графика, то следует нанести ещё несколько точек кривой в тех местах, где течение графика менее ясно.
Пример 17. Построить график функции 
.
Решение.
1. Область существования функции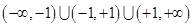 
.
2. График функции с осями координат не пересекается.
3. Функция не является периодической.
4. 
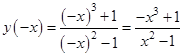. Функция не является ни четной, ни нечетной.
5. Найдем промежутки возрастания и убывания функции, точки экстремума.
.
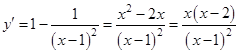. Критические точки 
Имеем:
| - график функции возрастает; |
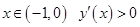
| - график функции возрастает; |
| - график функции убывает; |
| - график функции убывает; |
| - график функции возрастает. |
При переходе через точку 
производная меняет знак с + на 
, поэтому функция в точке имеет максимум, 
. При переходе через точку 
производная меняет знак с на +, функция в точке имеет минимум, 
.
6. Найдём промежутки выпуклости и вогнутости графика функции, точки перегиба.
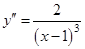. При 
- график функции выпуклый; 
- график функции выпуклый;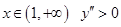 
- график функции вогнутый.
7. Асимптоты для данной функции найдены в примере 16. Прямая 
- двухстороння вертикальная асимптота.
Полученные результаты запишем в таблице.
| 
| 
| 
| 
| 
| 
| |||
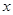
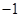
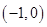
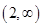
| + | не сущ | + |
| не сущ |
| + | ||
|
| не сущ |
|
|
| не сущ | + | + | + |
| 
| не сущ |
| max
| 
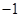
| не сущ | 
| min | 
|
Рис. 2
Исследовать и построить графики следующих функций.
62. 
| 69. 
|
63. 
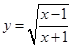
| 70. 
|
64. 
| 71.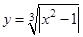 
|
65. 
| 72. 
|
66. 
| 73. 
|
67. 
| 74. 
|
68. 
| 75. 
|
Использованная литература
1. Г.С. Бараненков, Б.П. Демидович и др. «Задачи и упражнения по математическому анализу» для втузов, «Наука», Москва, 1970 г.
2. В.А. Болгов, Б.П. Демидович, В.А. Ефименко, А.В. Ефимов и др. «Сборник задач по математике» для втузов, Т1, «Наука», Москва, 1981 г.
3. П.П. Коровкин «Математический анализ», «Просвещение», Москва, 1972 г.
4. А.Ф. Бермант, И.Г. Араманович «Краткий курс математического анализа», «Наука», Москва, 1973 г.
