Экспериментальные измерения частотных характеристик последовательной R–С- цепи проводят аналогично экспериментальным измерениям частотных характеристик последовательной R–L- цепи. После выполнения предварительных настроек следует собрать схему из последовательно соединенных между собой ёмкости  и сопротивления
и сопротивления 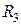 в соответствии с рис. 18. Для этого переключатель 3 (рис. 3) В1 на панели управления макетом установить в положение 2 (передача сигнала со входа переключателя на его выход без изменений). Переключатель 4 (рис. 3) В2 установить в положение 0 (никакие цепи, управляемые этим переключателем, не подключены). Переключатель 5 (рис. 3) В3 установить в положение 8, соответствующее последовательному включению в цепь ёмкости
в соответствии с рис. 18. Для этого переключатель 3 (рис. 3) В1 на панели управления макетом установить в положение 2 (передача сигнала со входа переключателя на его выход без изменений). Переключатель 4 (рис. 3) В2 установить в положение 0 (никакие цепи, управляемые этим переключателем, не подключены). Переключатель 5 (рис. 3) В3 установить в положение 8, соответствующее последовательному включению в цепь ёмкости  . Переключатель 6 (рис. 3) В4 установить в положение 5, соответствующее последовательному подключению сопротивления
. Переключатель 6 (рис. 3) В4 установить в положение 5, соответствующее последовательному подключению сопротивления 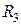 в исследуемую цепь.
в исследуемую цепь.
Собрав указанным образом последовательную цепь R 3 –C 22, следует провести измерения величины действующего значения выходного напряжения 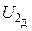 на выходе макета (это напряжение
на выходе макета (это напряжение  на сопротивлении
на сопротивлении 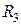 ) для частот от 2 до 20 кГц с шагом 1 кГц аналогично тому, как это было выполнено ранее для последовательнойцепи L 13 –R 3. Результаты измерений для заданного диапазона частот следует занести в табл. 8.
) для частот от 2 до 20 кГц с шагом 1 кГц аналогично тому, как это было выполнено ранее для последовательнойцепи L 13 –R 3. Результаты измерений для заданного диапазона частот следует занести в табл. 8.
Таблица 8
Экспериментальные значения выходного напряжения последовательной цепи R 3 –C 22
Частота 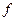 , кГц , кГц
| |||||||||||||||||||
| Параметр | |||||||||||||||||||
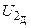 , В , В
|
При проведении измерений для последовательной цепи R 3 –C 22 следует иметь в виду, что величины напряжений на выходе макета могут оказаться малыми по абсолютной величине (десятки и даже единицы мВ). В этом случае переключателем 3 (рис. 5) следует установить чувствительность вольтметра порядка мВ. Таким образом окажется измеренной амплитудно-частотная характеристика (АЧХ) выходного напряжения последовательной цепи R 3 –C 22 в диапазоне частот от 2 до 20 кГц с шагом 1 кГц.
После проведения экспериментальных измерений следует произвести обработку полученных данных. Для этого, используя результаты измерений, занесенные в табл. 8, рассчитать частотные зависимости:
модуля действующего значения тока в цепи  ;
;
модуля действующего значения напряжения на ёмкости  ;
;
модуля действующего значения напряжения на сопротивлении  ;
;
модуля входного сопротивления цепи 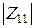 ;
;
величины модуля реактивного сопротивления ёмкости 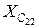 ;
;
величины ёмкости  ;
;
фазового сдвига между напряжением и током на входе цепи  .
.
Для определения заданных характеристик последовательной цепи R 3 –C 22 необходимо построить векторную диаграмму напряжений (треугольник напряжений) и векторную диаграмму сопротивлений (треугольник сопротивлений) этой цепи аналогично тому, как это было сделано для последовательной R–L- цепи (рис. 11, 12).
Рассмотрим такое построение. Основой (осью) векторной диаграммы напряжений последовательной цепи R 3 –C 22 является вектор тока  , так как цепь последовательная и ток является общим для всех элементов цепи в данный момент времени на данной частоте. Момент времени, для которого строится векторная диаграмма, возьмем нулевым
, так как цепь последовательная и ток является общим для всех элементов цепи в данный момент времени на данной частоте. Момент времени, для которого строится векторная диаграмма, возьмем нулевым  , чтобы ось векторной диаграммы располагалась горизонтально.
, чтобы ось векторной диаграммы располагалась горизонтально.
Вдоль оси тока  в принятом масштабе напряжений откладываем значение падения напряжения на активном сопротивлении
в принятом масштабе напряжений откладываем значение падения напряжения на активном сопротивлении  , так как ток и напряжение на сопротивлении связаны законом Ома, и сдвига фаз между ними нет. Падение напряжения на ёмкости откладываем от конца вектора
, так как ток и напряжение на сопротивлении связаны законом Ома, и сдвига фаз между ними нет. Падение напряжения на ёмкости откладываем от конца вектора  в виде вектора
в виде вектора  , отстающего от вектора
, отстающего от вектора  на
на  (перпендикулярно вниз), так как напряжение на ёмкости отстает от тока на эту величину. Соединив начало координат с концом вектора
(перпендикулярно вниз), так как напряжение на ёмкости отстает от тока на эту величину. Соединив начало координат с концом вектора  , получим значения напряжения на входе цепи
, получим значения напряжения на входе цепи 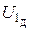 и сдвига фаз
и сдвига фаз  между напряжением и током в цепи R 3 –C 22 (рис. 21).
между напряжением и током в цепи R 3 –C 22 (рис. 21).

Рис. 21. Векторная диаграмма напряжений последовательной цепи R 3 –C 22 (треугольник напряжений)
Модуль действующего напряжения на ёмкости  можно найти, зная действующее значение входного напряжения на цепи
можно найти, зная действующее значение входного напряжения на цепи 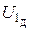 (равно 1 В), векторную диаграмму напряжений (рис. 21) последовательной цепи R 3 –C 22 и величину действующего значения напряжения на сопротивлении
(равно 1 В), векторную диаграмму напряжений (рис. 21) последовательной цепи R 3 –C 22 и величину действующего значения напряжения на сопротивлении  из табл. 8:
из табл. 8:
 . (63)
. (63)
Сдвиг фаз между входным напряжением и током  в последовательной цепи R 3 –C 22 тогда равен
в последовательной цепи R 3 –C 22 тогда равен
 . (64)
. (64)
Поделив все стороны треугольника напряжений последовательной цепи R 3 –C 22 (рис. 21) на общий для них параметр – ток  , получим треугольник сопротивлений для этой цепи (рис. 22). При этом реактивное сопротивление ёмкости
, получим треугольник сопротивлений для этой цепи (рис. 22). При этом реактивное сопротивление ёмкости 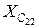 можно найти, зная напряжение
можно найти, зная напряжение  на ёмкости из выражения (63) и ток цепи
на ёмкости из выражения (63) и ток цепи  из выражения (56):
из выражения (56):
 . (65)
. (65)
С другой стороны, из треугольника сопротивлений величину модуля реактивного сопротивления ёмкости 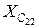 можно найти по выражению
можно найти по выражению
 , (66)
, (66)
что позволит определить величину и самой ёмкости  :
:
 . (67)
. (67)
Экспериментальную величину модуля входного сопротивления цепи 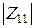 можно найти, зная напряжение
можно найти, зная напряжение  на ёмкости (63) и на сопротивлении
на ёмкости (63) и на сопротивлении  (табл. 8), или действующее значение входного напряжения на цепи
(табл. 8), или действующее значение входного напряжения на цепи 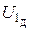 (равно 1 В), а также величину тока цепи
(равно 1 В), а также величину тока цепи  (56):
(56):
 . (68)
. (68)
Экспериментальную величину сдвига фаз между входным напряжением и током  в последовательной цепи R 3 –C 22 также можно узнать, воспользовавшись графическими построениями векторной диаграммы напряжений цепи рис. 21, через напряжение
в последовательной цепи R 3 –C 22 также можно узнать, воспользовавшись графическими построениями векторной диаграммы напряжений цепи рис. 21, через напряжение  на ёмкости (63) и на сопротивлении
на ёмкости (63) и на сопротивлении  (табл. 8):
(табл. 8):
 . (69)
. (69)

Рис. 22. Векторная диаграмма сопротивлений последовательной цепи R 3 –C 22 (треугольник сопротивлений)
Результаты вычислений частотных зависимостей величин  ,
,  ,
,  ,
, 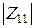 ,
, 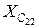 ,
,  ,
,  , следует свести в табл. 9.
, следует свести в табл. 9.
По результатам, сведенным в табл. 9, построить графики частотных зависимостей величин  ,
,  ,
,  ,
, 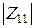 ,
, 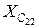 ,
,  ,
,  . Частотные зависимости величин
. Частотные зависимости величин  ,
,  ,
,  ,
, 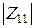 ,
,  построить на тех же осях, что ранее соответствующие теоретические зависимости (см. табл. 3).
построить на тех же осях, что ранее соответствующие теоретические зависимости (см. табл. 3).
Таблица 9
Экспериментальные параметры последовательной цепи R 3 –C 22
Частота 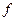 , кГц , кГц
| |||||||||||||||||||
| Параметр | |||||||||||||||||||
 , А , А
| |||||||||||||||||||
 , В , В
| |||||||||||||||||||
 , В , В
| |||||||||||||||||||
 , Ом , Ом
| |||||||||||||||||||

| |||||||||||||||||||
 , Ом , Ом
| |||||||||||||||||||
 , град , град
|
Построить векторные диаграммы напряжений и сопротивлений последовательной цепи R 3 –C 22 для трех частот:  кГц,
кГц,  кГц,
кГц, 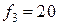 кГц.
кГц.






